Características de lentes divergentes, elementos, tipos, aplicações

As lentes divergentes são aqueles que são mais finos em sua parte central e mais espessa nas bordas. Como conseqüência, eles separam (diverge) os raios de luz que os afetam em paralelo ao eixo principal. Suas extensões acabam convergindo na imagem de foco localizada à esquerda da lente.

Lentes divergentes, ou negativas, como são conhecidas, formam o que é chamado de imagens virtuais de objetos. Eles têm várias aplicações. Em particular, na offtamologia, eles são usados ​​para corrigir a miopia e alguns tipos de astigmatismo.

Randrijo87 [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenças/BY-SA/4.0)]

Então, se você sofre de miopia e usa óculos, você tem um exemplo perfeito de lente divergente.

[TOC]

Características de lentes divergentes

Como explicado acima, as lentes divergentes são mais estreitas em sua parte central do que nas bordas. Além disso, nesse tipo de lentes, uma de suas superfícies é sempre côncava. Isso fornece a esse tipo de lentes uma série de características.

Para começar, o prolongamento dos raios que os afeta resulta em imagens virtuais que não podem ser coletadas em qualquer tipo de tela. É assim, porque os raios que cruzam as lentes não convergem em nenhum momento, pois divergem em todas as direções. Além.

Outra característica importante desse tipo de lentes é que o foco está à esquerda da lente, de modo que ela é entre isso e o objeto.

Além disso, em lentes divergentes, as imagens são menores que o objeto e estão entre isso e o foco.

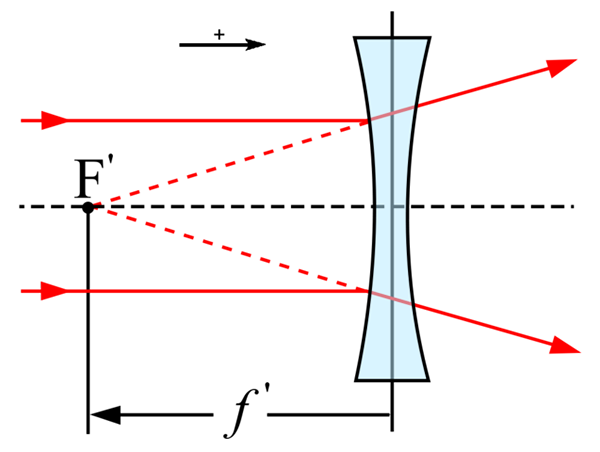Jipaul / de Henrik [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

Elementos de lentes divergentes

Ao estudá -los, é essencial saber quais elementos constituem as lentes em geral e as lentes divergentes em particular.

É chamado de centro óptico de uma lente até o ponto pelo qual os raios não experimentam nenhum desvio. O eixo principal, por outro lado, é a linha que se junta a esse ponto e o foco principal, sendo este último representado com a letra f.

Pode atendê -lo: fonte de tensão

O foco principal recebe o ponto em que todos os raios que afetam a lente em paralelo ao eixo principal são encontrados.

Dessa maneira, a distância entre o centro óptico e o foco é chamado de distância focal.

Os centros de curvatura são definidos como os centros das esferas que criam a lente; sendo, dessa maneira, os rádios da curvatura os rádios das esferas que dão origem à lente. E, finalmente, o plano central da lente é chamado de plano óptico.

Formação de imagem

Para representar graficamente a formação de uma imagem em uma lente fina, é necessário saber apenas a direção que dois dos três raios seguirão
cuja trajetória é conhecida.

Um deles é aquele que afeta a lente em paralelo ao eixo óptico da lente. Isso, uma vez refratado na lente, passará pela imagem do foco. O segundo dos raios cuja trajetória é conhecida é a que atravessa o centro óptico. Isso não verá sua trajetória modificada.

O terceiro e o último é o que passa pelo foco do objeto (ou seu prolongamento atravessa o foco do objeto) que após a refratação seguirá uma direção paralela à do eixo óptico da lente.

Dessa forma, em geral, um tipo de imagem ou outro será formado nas lentes, dependendo da posição do objeto ou corpo em relação à lente.

No entanto, no caso particular de lentes divergentes, qualquer que seja a posição do corpo em frente da lente, a imagem que será formada terá certas características. E em lentes divergentes, a imagem sempre será virtual, menor que o corpo e a direita.

Pode atendê -lo: número de fluxo: como é calculado e exemplos

Formulários

O fato de eles podem separar a luz que os atravessa dá lentes divergentes algumas qualidades interessantes no campo da óptica. Dessa forma, eles podem corrigir a miopia e alguns tipos específicos de astigmatismo.

As lentes oftálmicas divergentes separam os raios da luz para que, quando atingissem o olho humano, sejam mais distanciados. Assim, quando eles passam pela córnea e pelas lentes, eles vão além e podem alcançar a retina, executando os problemas de visão das pessoas que sofrem de miopia.

Pessoal

Como já mencionamos, as lentes convergentes têm pelo menos uma superfície côncava. Por isso, existem três tipos de lentes divergentes: Bicócavas, Planocóvas e Convexo-Cócavas.

As lentes divergentes de Bicócavas são compostas por duas superfícies côncavas, as plâncas têm uma côncavo e uma superfície plana, enquanto no menisco divergente convexo uma superfície é levemente convexa e o outro é côncavo.

Diferenças com lentes convergentes

Nas lentes convergentes, ao contrário do que acontece em divergente, a espessura diminui do centro para as bordas. Assim, nesse tipo de lente, os raios de luz que afetam o eixo principal em paralelo estão concentrados ou converge no único ponto (no foco). Dessa forma, eles sempre criam imagens reais de objetos.

Na óptica, lentes convergentes ou positivas são usadas principalmente para corrigir a vista farsia, presbiopia e alguns tipos de astigmatismo.

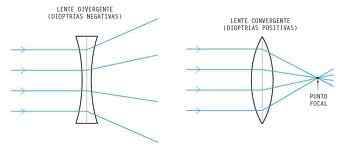GrantExgator [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

Equação de Gauss das lentes e aumento da lente

O tipo de lente que é estudado geralmente é chamado de lentes finas. Assim, todas as lentes cuja espessura é muito pequena em comparação com os rádios de curvatura das superfícies que os limitam são definidos.

O estudo desse tipo de lentes pode ser realizado principalmente por meio de duas equações: a equação de Gauss e a equação que permite determinar o aumento da lente.

Equação de Gauss

A importância da equação de Gauss das lentes finas está no grande número de problemas ópticos básicos que permitem resolver. Sua expressão é a seguinte:

Pode atendê -lo: galáxias elípticas: formação, características, tipos, exemplos

1/f = 1/p +1/q

Onde 1/ f é a potência da lente e F é a distância focal ou a distância do centro óptico para o focam. A unidade de medida do poder de uma lente é a dioptria (d), sendo o valor de 1 d = 1 m^-1. Por outro lado, P e Q são, respectivamente, a distância em que um objeto e a distância em que sua imagem é observada.

Exercício resolvido

Um corpo é colocado 40 centímetros de uma lente divergente de -40 centímetros de distância focal. Calcule a altura da imagem se a altura do objeto for 5 cm. Determine também se a imagem está certa ou invertida.

Temos os seguintes dados: H = 5 cm; P = 40 cm; F = -40 cm.

Esses valores são substituídos na equação de Gauss das lentes finas:

1/f = 1/p +1/q

E é obtido:

1/-40 = 1/40 +1/q

Onde Q = - 20 cm

Em seguida, substituímos o resultado obtido anteriormente na equação do aumento de uma lente:

M = - Q / P = - -20 / 40 = 0,5

Obter que o valor do aumento é:

M = H '/H = 0,5

Limpando esta equação h ', que é o valor da altura da imagem, ela atinge:

H '= h/2 = 2,5 cm.

A altura da imagem é 2.5 cm. Além disso, a imagem está certa desde M> 0 e diminuiu, pois o valor absoluto de M é menor que 1.

Referências

1. Luz (n.d.). Na Wikipedia. Recuperado em 11 de abril de 2019, deste.Wikipedia.org.
2. Lekner, John (1987). Teoria da reflexão, de ondas eletromagnéticas e parlamentares. Springer.
3. Luz (n.d.). Na Wikipedia. Recuperado em 11 de abril de 2019, de.Wikipedia.org.
4. Lente (n.d.). Na Wikipedia. Recuperado em 11 de abril de 2019, deste.Wikipedia.org.
5. Lente (óptica). Na Wikipedia. Recuperado em 11 de abril de 2019, de.Wikipedia.org.
6. Atos, Eugene (2002). Óptica (4ª ed.). Addison Wesley.
7. Tupler, Paul Allen (1994). Físico. 3ª edição. Barcelona: Eu revertei.