Interpolação linear

Nós explicamos qual é a interpoação linear, suas fórmulas, como fazer uma, com exemplos e exercícios resolvidos

O que é interpolação linear?

O Interpolação linear Consiste em estimar a localização de um ponto dentro de um intervalo numérico, assumindo que os valores extremos desse intervalo são unidos por uma linha. Conhecido a equação desta linha, é possível localizar o ponto desconhecido.

A idéia é esquematizada na figura a seguir, que mostra uma abordagem do gráfico de uma função entre os pontos a e b. Supondo que esses pontos estejam próximos, é possível aproximar a curva que os une através de uma linha e, assim, encontrando os pontos intermediários.

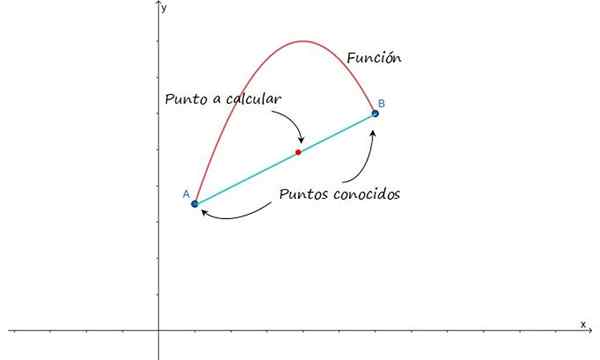figura 1.- Para fazer uma interpolação linear entre os pontos A e B, deve -se assumir que eles estão unidos por uma linha . Fonte: f. Zapata.

Você também pode aproximar a curva que se une aos pontos dados por meio de uma função quadrática ou outro polinômio. No entanto, a linha tem a vantagem de sua simplicidade matemática, por isso é fácil de lidar, embora seja a interpolação mais simples de todos, é possível que o resultado não seja tão preciso quanto o obtido usando outras funções.

Fórmulas

Existem dois pontos de coordenadas [x_qualquer, f (x_qualquer)] e [x₁, f (x₁)] entre os quais está o ponto [x, g (x)], cujas coordenadas são desejadas para saber.

O primeiro passo consiste em ingressar nos pontos conhecidos através de um segmento de linha, no qual as coordenadas do ponto um calcular são encontradas.

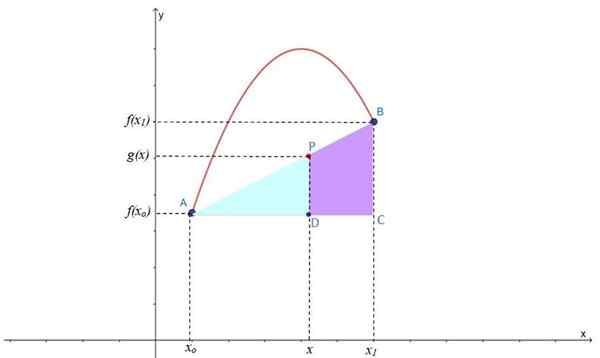Figura 2.- Interpolação linear para encontrar o ponto P na linha de interfocação G (x), localizada entre os pontos A e B de F (x). Fonte: f. Zapata.

Como você pode ver, dois retângulos são formados: ABC e APD, que também têm um ângulo agudo em comum, de modo que são triângulos semelhantes, aos quais o teorema de Thales pode ser aplicado:

Pode atendê -lo: geometria analítica

Substituindo a medida dos segmentos de acordo com o gráfico, é obtido o seguinte relacionamento:

A partir daí, procedemos para limpar G (x):

 Chamando:

F₁(x₁) = y₁ ; F_qualquer(x_qualquer) = y_qualquer ; g (x) = y

A equação superior é transformada em:

Margem de erro

Quando uma função está se aproximando desse método, o nível de erro é dado pelo valor absoluto da diferença entre a função f (x) e a linha de interpolação G (x):

Erro = │f (x) - g (x) │

Como fazer interpolação linear?

A realização de uma interpolação linear é muito simples, você só precisa seguir estas etapas:

Passo 1

Determine o ponto desconhecido P (x, y).

Passo 2

Estabeleça os dois pontos que limitam o intervalo em que o valor a ser calculado está localizado, ou seja, os pontos (x x_qualquer,e_qualquer) e (x₁, e₁).

etapa 3

Substitua todos os valores na equação:

E calcule o resultado.

Exemplos de interpolação linear

Exemplo 1

Você deseja encontrar o valor aproximado do LN 3 através da interpolação linear, dados os seguintes valores:

ln 2 = 0.693147 e LN 4 = 1.386294

Compare o resultado com o valor de LN 3 obtido através de uma calculadora e determine a margem comprometida.

• Passo 1

Para encontrar o valor aproximado do LN 3, você deve prosseguir com a seguinte maneira: Primeiro, o desconhecido é estabelecido, que é y = ln 3, próximo ao seu valor correspondente de "x": x = 3. Este é o ponto em que você deseja calcular: (3, ln 3).

• Passo 2

Então você deve estabelecer os pontos limitados do intervalo com os valores conhecidos. É solicitado a fazê -lo com os próximos dois pontos:

• Limite inferior: [x_qualquer = 2; e_qualquer = ln 2 = 0.693147]
• Limite superior: [x₁ = 4; e₁ = ln 4 = 1.386294]

• etapa 3

Os valores determinados nas etapas 1 e 2 são cuidadosamente substituídos na equação para gerar o resultado da abordagem do LN 3:

Pode atendê -lo: quantas soluções uma equação quadrática tem?

O valor real do LN 3 obtido pela calculadora é:

ln 3 = 1.098612

E a margem de erro é:

Erro = │1.098612 - 1.03971 │ = 0.059

O erro percentual da interpolação é calculado dividindo o erro entre o valor real do LN3 e a multiplicação por 100 %:

Erro percentual = (erro real/valor) × 100 = (0.059/1.098612) × 100% = 5.4%

Exemplo 2

Agora você deseja encontrar o valor aproximado do LN 3 por interpolação linear, conhecida esses dois valores:

LN 2.5 = 0.916291 e LN 3.5 = 1.252763

Determine também o erro correspondente e compare com os resultados do exemplo anterior.

• Passo 1

Novamente, o ponto desconhecido é:

y = ln 3, x = 3

• Passo 2

• Limite inferior: [x_qualquer = 2.5; e_qualquer = y_qualquer = ln 2.5 = 0.916291]
• Limite superior: [x₁ = 3.5; e₁ = ln 3.5 = 1.252763]

• etapa 3

Examinando o valor oferecido pela calculadora:

ln 3 = 1.098612

O nível de erro é determinado neste caso, que resulta:

Erro = │1.098612 - 1.084527 │ = 0.014

O erro percentual neste caso é ≈ 1.3 %. Comparando com o nível de erro do Exemplo 1, o novo valor é mais preciso, uma vez que o intervalo escolhido para interpolar é menor.

Exercícios resolvidos

Exercício 1

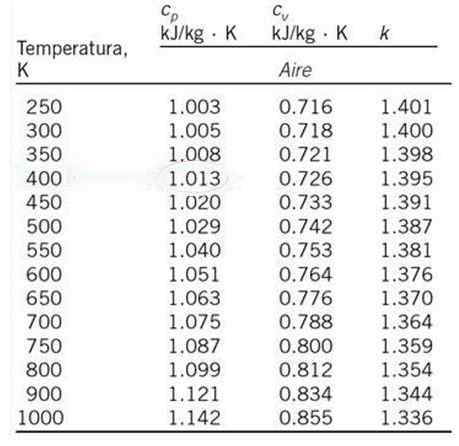
Calcule, por interpolação linear, o calor específico do ar a pressão constante c_p  e temperatura de 530 K, a partir da tabela de valores mostrados abaixo.

• Solução

Na resolução de muitos problemas, é comum que o valor procurado não apareça exatamente como desejado na tabela de valores em mãos. Uma alternativa é escolher o valor mais próximo do desejado, mas muitas vezes uma interpolação linear é suficiente para encontrar uma abordagem muito melhor.

Pode atendê -lo: sinais de agrupamento

O valor de c_p Um 530 K não aparece na tabela anexada, mas uma interpolação linear pode ser feita com os respectivos aquecimentos específicos a 500 K e 550 K, que são as temperaturas mais próximas de 530 K e cujos aquecimentos específicos aparecem na tabela mostrada.

Os respectivos calor específicos de calor para essas temperaturas são:

T_qualquer = 500 K; c_po = 1.029 kJ /kg ∙ k

T₁ = 550 k; c_P1 = 1.040 kJ /kg ∙ k

E o desconhecido é o ponto (500k, c_p)

Substituindo na fórmula da interpolação linear dada acima, com T na cena da variável "X" e C_p Em vez de "y", você tem:

Exercício 2

A carga aplicada a uma mola (em Kilopondios) produz os seguintes alongamentos (em milímetros) de acordo com a tabela mostrada:

Calcule o alongamento quando a carga for 12.6 kp.

• Solução

Let e ​​o valor do alongamento procurado quando a carga é C = 12.6 kp. O ponto desconhecido é (12.6, y), que está entre os pontos:

C_qualquer = 10 kp; e_qualquer = 105 mm

C₁ = 15 kp; e₁ = 172 mm

Resta apenas substituir os valores na equação:

Exercício proposto

Calcule o calor específico de calor até um volume constante para uma temperatura de 727 K, usando interpolação linear e a tabela de valores mobiliários do exercício resolvido 1.

Referências

1. Academia Rafa Vilchez. Como realizar interpolação linear. Recuperado de: academiraafavilchez.com
2. Chapra, s. 2007. Métodos numéricos para engenheiros. 5 ª. Edição. McGraw Hill.
3. Academia Khan. Matemática da interpolação linear. Recuperado de: Khanacademy.org.
4. A vida educacional. Fórmula de interpolação linear. Recuperado de: TeeducationLife.com
5. Engenheiro X. Interpolação linear e extrapolação com calculadora. Recuperado de: X-Engineer.org.