Igualdade matemática
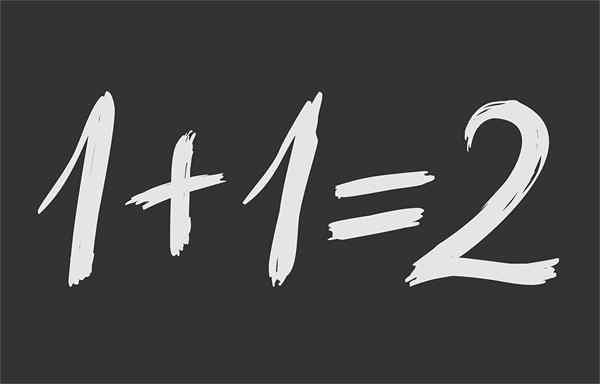
- 4480
- 137
- Melvin Mueller
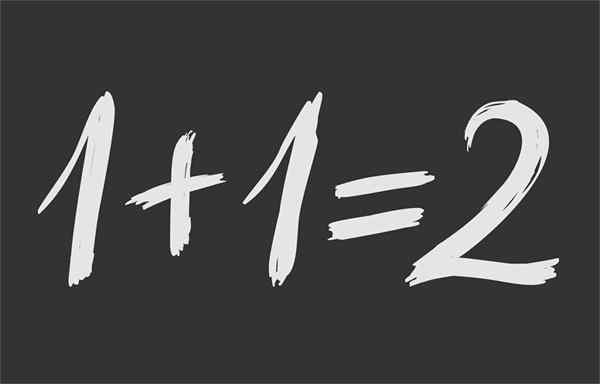 figura 1.- A igualdade matemática garante que 1 + 1 seja o mesmo 2
figura 1.- A igualdade matemática garante que 1 + 1 seja o mesmo 2 O que é igualdade matemática?
Uma igualdade matemática garante que duas expressões sejam iguais ou diferentes, elas são totalmente equivalentes. Essas expressões podem ser natureza diversa, por exemplo, números, letras que simbolizam quantidades ou magnitudes, combinações de números e letras, matrizes e mais.
O símbolo usado para denotar a igualdade na linguagem matemática é a de duas linhas paralelas e horizontais, que no texto impresso é o símbolo bem conhecido "=". Por exemplo, se você tiver três maçãs, pode escrever a seguinte igualdade:
Número de maçãs = 3
A frase "número de maçãs" é o membro da esquerda e o número 3 é o membro à direita da igualdade.
Como é possível escrever quantidades numéricas de várias maneiras, a igualdade é usada para denotá -las. Tomando um caso específico para ilustrar o ponto, existem várias maneiras de escrever o número 4, além do mais óbvio que é 4 = 4, o seguinte pode ser escrito, através de uma igualdade matemática:
2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
22 = 4
A igualdade mostrada aqui é verdadeira, mas uma igualdade pode não ser, por exemplo, 10 + 5 = 20 é falsa, pois 10 + 5 = 15.
Certamente o leitor conhece outras maneiras de escrever o número 4. Observe que as expressões de cada lado da igualdade podem ser números, palavras, letras que simbolizam quantidades ou outros símbolos, por exemplo:
x + 1 = 7
para2B - 1 = xy
f (x) = 2x2
Os matemáticos nem sempre usaram o símbolo da igualdade, então os antigos tratados de matemática eram muito extensos.
É atribuído ao matemático e ao doutor Robert Remember (1510-1558), nascido no País de Gales, a criação do símbolo da igualdade "=", tão familiar a todos hoje. Lembre -se, aparentemente cansado de escrever o tempo todo, a frase "exatamente como" em um de seus tratados de matemática, ele decidiu abreviar em seu lugar os parentes paralelos listras.
Pode servir a você: Prisma pentagonal: características, peças, vértices, bordas, volumePropriedades da igualdade matemática
As propriedades a seguir permitem funcionar corretamente com a igualdade matemática. Eles são axiomáticos, então não exigem demonstração:
1.- Propriedade reflexiva
Esta propriedade estabelece que qualquer quantidade é igual a si mesma. Em particular, como qualquer número é igual a si mesmo, os iguais podem ser escritos:
5 = 5
36.35 = 36.35
Se uma quantidade for literal ou é uma combinação de letras e números, também é igual a si mesma:
3x = 3x
para2Bc-1 = a2Bc-1
2.- Propriedade da simetria
Os valores ou membros de ambos os lados da igualdade podem ser trocados sem validade perdida. Ou seja, se o que está à esquerda do símbolo "=" é escrito à sua direita, e o que está à sua direita é colocado à esquerda, é a mesma igualdade.
Por exemplo, a expressão 5 + 2 = 7 é equivalente a este: 7 = 5 + 2. Da mesma maneira:
12 + 8 = 20; 20 = 12 + 8
x + 1 = 3; 3 = x + 1
x - z = y; y = x - z
3.- Propriedade transitiva
Esta propriedade refere -se à equivalência da igualdade. Se duas iguais têm um membro comum, eles também são os mesmos, pois em geral:
Se "x = y" e "y = z" então x = z =
Para ilustrar esta propriedade, considere essas duas igualidades numéricas: 2 + 2 = 4 e 6 - 2 = 4. Como ambos são iguais a 4 (eles têm um membro comum), o seguinte pode ser escrito, sem perder qualquer validade:
2 + 2 = 6 - 2
Outro exemplo, desta vez com cartas:
Sim x + 1 = 5
E
A - B = 5
Então:
x+1 = a - b
4.- Propriedade de cancelamento
Uma igualdade não é alterada se nos dois membros houver a mesma quantidade que está adicionando (ou subtraindo) e é decidido eliminar ou cancelar. Esta é a propriedade de cancelamento da soma.
Tome como exemplo a seguinte igualdade numérica em que os 10 aparecem tanto no membro da direita quanto na esquerda:
Pode atendê -lo: funções trigonométricas: básico, no avião cartesiano, exemplos, exercícios2 + 2 + 10 = 6 - 2 + 10
O número 10 pode ser cancelado sem a igualdade perdendo sua validade, deixando outra igualdade mais curta e equivalente à anterior:
2 + 2 = 6 - 2
Na igualdade (10 ÷ 2) - 3 = 5 - 3 O número inteiro - 3 pertence a ambos os membros da igualdade e aparece como adicionando, portanto, pode ser cancelado, obtendo:
10 ÷ 2 = 5
Isso também acontece com quantidades literais, por exemplo:
Sim x + 2y + z = −a + b + z
Então o "Z" pode ser cancelado, pois é encontrado em ambos os lados da igualdade como adicionar (e com o mesmo sinal).
Ao fazer isso, resulta:
x + 2y = −a + b
Também pode definir a propriedade de cancelamento da multiplicação. Se a mesma quantidade C multiplicar os dois membros da igualdade, esse valor poderá ser cancelado, por exemplo:
Cx = cy
Então C pode ser cancelado para obter simplesmente:
x = y
5.- Propriedade de uniformidade
Uma igualdade permanece invariável ao adicionar, subtrair, multiplicar ou dividir pela mesma quantidade em ambos os lados do mesmo.
Por exemplo, ele tem para 8 + 5 = 13, se ambos os membros se multiplicarem por um determinado número arbitrário C = 2, a igualdade permanece:
(8+5) × 2 = 13 × 2
13 × 2 = 26
Classes iguais matemáticas
Existem vários tipos de igualdade matemática, por isso são classificados para o seu melhor entendimento em:
-Identidades, Eles são a igualdade em que ambos os membros são idênticos:
2 = 2
x = x
2x = x + x
e assim por diante.
-Equações, Essas são iguais em que uma ou mais incógnitas aparecem e são verdadeiras para certos valores, ou seja, a igualdade não é atendida por nenhum valor arbitrário, portanto também são conhecidos como igualdade condicional. Exemplos:
x + 1 = 5
x3 = 27
A + b = 40
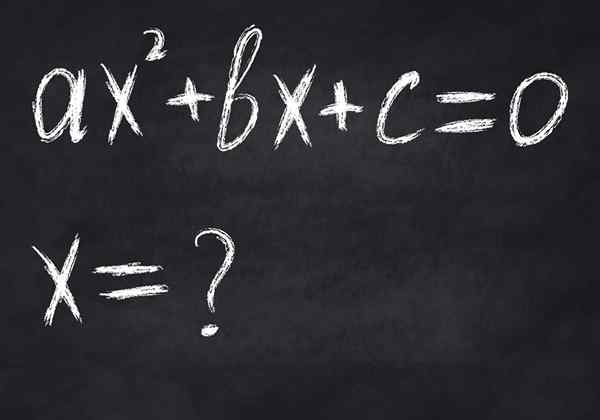 Figura 2.- Uma equação é uma igualdade matemática condicional, pois é atendida apenas para certos valores variáveis. A imagem mostra uma equação de segundo grau, que no máximo tem duas soluções reais
Figura 2.- Uma equação é uma igualdade matemática condicional, pois é atendida apenas para certos valores variáveis. A imagem mostra uma equação de segundo grau, que no máximo tem duas soluções reais -Equivalências, Neles, o membro da esquerda é equivalente ao da direita, mesmo que não sejam iguais, por exemplo em: 23 = 8.
Pode atendê -lo: princípio aditivo-Fórmulas, É uma igualdade que é sempre cumprida para os valores da variável independente, como na fórmula bem conhecida para a distância d, dependendo do tempo t de um celular com movimento retilíneo uniforme: D = v ∙ t
Exercícios resolvidos
Exercício 1
Escreva o número 10 a quatro igualdade diferente e equivalente.
Solução
Toda essa igualdade expressa o número 10, mas de maneiras diferentes:
5 × 2 = 10
11-1 = 10
101= 10
20 ÷ 2 = 10
Exercício 2
Qual é o valor de x que satisfaz a igualdade x + 1 = 3?
Solução
Esta igualdade é uma equação, uma vez que o valor de x é desconhecido. Usando a propriedade 5, se a expressão x + 1 = 3 for adicionada (−1) em ambos os lados do símbolo "=", a igualdade permanece:
x + 1 + (−1) = 3 + ( - 1)
Ao adicionar (-1) ao membro da esquerda e a operação é resolvida, o "x" está sozinho no lado esquerdo da igualdade, este procedimento é chamado liberação:
x + 1 - 1 = 3−1
x = 2
Portanto, o valor que satisfaz essa igualdade é x = 2.
Exercício 3
Se um celular com movimento retilíneo uniforme tem uma velocidade de 2.5 m/s, qual é a distância que percorre 3 segundos?
Solução
A fórmula vista na seção anterior é usada, D = v ∙ t, em que o valor de V é substituído:
D = 2.5 ∙ t
A expressão se torna uma igualdade quando t = 3 segundos e a operação é resolvida:
D = 2.5 ∙ 3 m = 7.5m
O que resulta em igualdade:
D = 7.5m
Referências
- Barnett, r. 2000. Pré-escultura. 4º. Edição. McGraw Hill.
- Larson, r. 2012. Pré-escultura. 8º. Edição. Cengage Learning.
- Pérez, v. Propriedades da igualdade algébrica. Recuperado de: matemática.LaGuia2000.com.
- Propriedades da igualdade. Recuperado de: PPS.K12.Ou.nós.
- Stewart, J. 2007. Pré-cálculo: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.

