Identidades trigonométricas (exemplos e exercícios)

As Identidades trigonométricas Essas são as relações entre razões trigonométricas, que são verdadeiras para qualquer valor da variável. Por exemplo:

Tan θ = sin θ /cos θ

É uma identidade trigonométrica que relaciona três razões do ângulo θ, a tangente, a mama e o cosseno do referido ângulo.

figura 1. Algumas identidades trigonométricas amplamente utilizadas no cálculo. Fonte: f. Zapata.

Essa identidade é verdadeira para todo valor, exceto aqueles que fazem 0 o denominador. O cos θ é 0 para θ = ± π/2, ± 3π/2, ± 5π/2… Outro exemplo de identidade trigonométrica é:

sin x . Sec x . Ctg x = 1

[TOC]

Demonstração

Existem duas maneiras básicas de demonstrar que uma identidade trigonométrica é verdadeira:

1- transformando um dos membros da igualdade no outro, através de manipulações algébricas convenientes.

2- Desenvolva os dois membros da igualdade separadamente, até que as respectivas expressões finais de cada um sejam exatamente iguais.

Na identidade proposta, vamos transformar o lado esquerdo da igualdade, para o qual expressamos CTG X e Sec X em termos de mama e cosseno da seguinte forma:

Ctg x = cos x / sen x

Sec x = 1 /cos x

Substituímos essa expressão no lado esquerdo da identidade e simplificamos:

sin x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . sin x) = 1

E a veracidade da identidade já está comprovada.

Tipos de identidades trigonométricas

Existem vários tipos de identidades trigonométricas. Em seguida, descreveremos brevemente os principais:

- Identidades trigonométricas fundamentais

Distinguimos dois tipos de identidades fundamentais:

I) Aqueles que são expressos através dos motivos básicos, cosseno e tangente:

• Sec x = 1 /cos x
• Dano x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) aqueles derivados da paridade. Sabemos através de seu gráfico que Sen X é uma função estranha, o que significa que:

Pode atendê -lo: 60 divisores

sin (-x) = - sin x x

Por sua parte, cos x é um casal, portanto:

cos (-x) = cos x

Então:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Igualmente:

• COTG (-x) = -ctg x
• sec (-x) = seg x
• dano (-x) = - dano x

- Identidades pitagóricas

Eles são os obtidos da aplicação do teorema de Pitágoras ao triângulo retângulo dos gatos A e B e Hipotenusa c. Vamos ver:

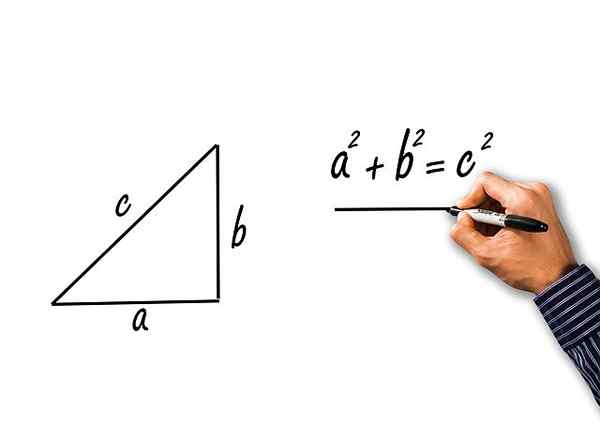Figura 2.- Do teorema de Pitágoras, as três identidades trigonométricas pitagóricas são obtidas. Fonte: Pixabay.

O teorema de Pitágoras afirma que:

c² = a² + b²

Dividindo tudo entre c²:

c² / c² = (a² / c²) + (B² / c²)

O termo à esquerda é 1 e lembrando que o seio e o cosseno do ângulo agudo α são definidos como:

sin α = a/c

cos α = b/c

Resultado:

1 = (sin α)² + (cos α)²

Esta identidade é conhecida como identidade fundamental.

O procedimento pode ser realizado dividindo -se entre² e B², O que dá origem a mais duas identidades:

Sec² α = 1 + tg² α

har² α = 1 + CTG² α

- Fórmulas para cosseno e o peito da soma/subtração de ângulos

As principais identidades trigonométricas para cosseno, mama e tangente da soma e subtração são os seguintes:

Demonstração de sen (α + β) e cos (α + β)

Essas identidades podem ser demonstradas geometricamente ou também através da fórmula de Euler:

e^Iα = cos α + i sin α

Vejamos o que acontece com a fórmula ao substituir a soma de dois ângulos α e β:

e^{I (α +β)} = cos (α + β) + i sin (α + β)

Essa expressão é complexa, sua parte real é cos (α + β) e sua parte imaginária é i sin (α + β). Mantemos esse resultado para usá -lo mais tarde e nos concentrar no desenvolvimento da parte exponencial:

e^{I (α +β)} = e^Iα ⋅ e^Iβ = (cos α + i sin α) . (cos β + i sin β) =

Pode atendê -lo: prisma hexagonal

= cos α⋅Cos β + cos α⋅i sen β + i⋅sen α cos β - sen α⋅sen β

A parte real dessa expressão é a que não é multiplicada pela unidade imaginária "i":

COS α⋅COS β - Sen α. Sen β

A parte imaginária, portanto, é:

I (cos α⋅sen β + sen α⋅Cos β)

Para que duas expressões complexas sejam as mesmas, a parte real de um deve ser igual à parte real do outro. O mesmo vale para partes imaginárias.

Tomamos o resultado salvo e comparamos com isso:

cos α. cos β - sen α. sin β = cos (α + β)

i (cos α⋅sen β + sen α⋅Cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sen α⋅COS β)

- Fórmulas para o ângulo duplo

Nas fórmulas anteriores, tomamos β = α e desenvolvemos:

sin (α + α) = sen 2 α = sen α⋅Cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sen α⋅sen α = cos = cos² α - sen ² α

TG (α + α) = Tg 2 α = [Tg α + Tg α] / [1- TG α⋅tg α] = 2tg α / 1- TG² α

Se na segunda expressão, os cos são substituídos² α = 1 - sen² α é obtido:

cos 2 α = cos² α- (1- cos² α) = 2 cos² α -1

- Fórmulas de meia -ângulo

Nesta última expressão, substituímos α por α/2, os seguintes restos:

cos α = 2 cos ²(α/2) -1

Limpeza:

Exercícios resolvidos

- Exercício 1

Mostre isso:

Solução

Nós vamos trabalhar algebricamente o termo restante para que pareça certo. Como no termo certo aparece sen x, o primeiro passo é expressar cos cos²X em termos de sen x para que tudo esteja em termos da mesma razão trigonométrica:

Pode servir a você: Fração equivalente a 3/5 (solução e explicação)

Então 1 - Sen é fator² x por ser uma diferença de quadrados perfeitos. Para fazer isso, ele limpa a partir da identidade fundamental:

cos²X = 1 - sen² x

1 - sen² x = (1- sin x) (1+senx)

E a fatoração na expressão original é substituída:

O termo (1- senx) é simplificado e permanece uma igualdade:

1 + sen x = 1 + senx

- Exercício 2

Resolva a seguinte equação trigonométrica e forneça a solução para valores entre 0 e 360º:

TG X + Sec² x = 3

Solução

No termo da esquerda, existem duas razões trigonométricas, portanto você deve reduzir tudo para um, para poder limpar o desconhecido. O termo sec² X é expresso através de uma das identidades pitagóricas:

Sec² α = 1 + tg² α

Substituindo a equação:

Tg x + 1 + tg² x = 3

Reorganizando os termos:

TG² x + tg x + 1 = 3

Esta equação é resolvida alterando a variável:

tg x = u

ou² + U + 1 - 3 = 0 → u² + U - 2 = 0

Esta equação de segundo grau é facilmente resolvida pela fatoração:

(U +2) (u-1) = 0

Portanto u₁ = -2 e você₂ = 1, equivalente a:

Tg x₁ = -2

Tg x₂ = 1

Finalmente:

x₁ = arctg (-2) = 296.6º

x₂  = arctg (1) = 45º

Referências

1. Carena, m. 2019. Manual de matemática da pré -universidade. Universidade Nacional da Costa.
2. Figuera, j. 1999. Matemática. 1º. Diversificado. Edições Bolivarianas Collegiate.
3. Hoffman, J. Seleção de questões de matemática. Volume 4.
4. Jiménez, r. 2008. Álgebra. Prentice Hall.
5. Wikipedia. Identidades e fórmulas de trigonometria. Recuperado de: é.Wikipedia.org.
6. Zapata, f. 4 maneiras de resolver uma equação de segundo grau. Recuperado de: Francesphysics.Blogspot.com.
7. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.