Funções e aplicações trigonométricas do círculo unitário

Ele Círculo unitário É um círculo de raio igual a 1, que geralmente é focado no ponto (0,0) do sistema de coordenadas cartesianas XY. É usado para definir facilmente as razões trigonométricas dos ângulos por retângulos.

A equação do círculo unitário focado na origem é:

x² + e² = 1

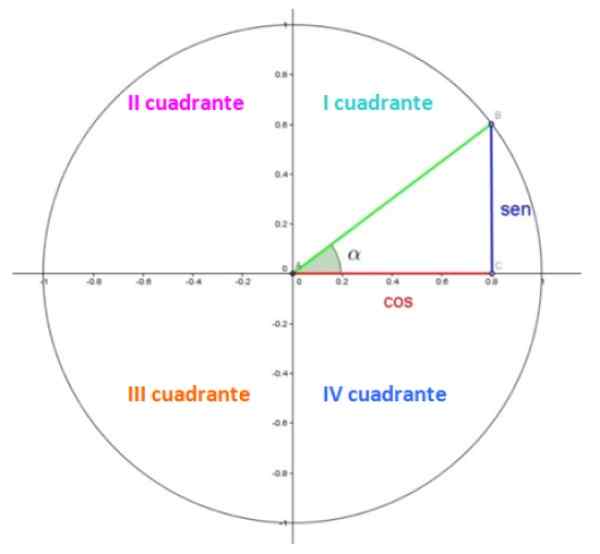
figura 1. O círculo unitário. Fonte: Wikimedia Commons.

Na Figura 1, temos o círculo unitário, no qual cada sala está em um quadrante. Os quadrantes são numerados com números romanos e são contados anti -marários.

No primeiro quadrante, há um triângulo. As categorias, em vermelho e em azul, respectivamente 0.8 e 0.6, enquanto a hipotenusa em verde mede 1, porque é um rádio.

O ângulo agudo α é um ângulo central na posição padrão, o que significa que seu vértice coincide com o ponto (0,0) e seu lado inicial com o eixo x positivo. O ângulo é medido contrário às mãos do relógio e, por convenção, é atribuído um sinal positivo.

Bem, no círculo unitário, as coordenadas de Coseno e o seno de α são respectivamente as coordenadas x e y do ponto B, que no exemplo mostrado são 0.8 e 0.6.

Desses dois, eles são definidos:

• tg α = sin α/cos α = 0.6/0.8 = 0.75
• Sec α = 1/ cos α = 1/0.8 = 1.25
• dano α = 1 / sin α = 1/0.6 = 1.66 ..
• ctg α = 1/tg = 0.8/0.6 = 1.33 ..

[TOC]

Aplicações do círculo unitário

Se nos limitarmos a retângulos, os motivos trigonométricos seriam aplicados apenas a ângulos agudos. No entanto, com a ajuda do círculo unitário, o cálculo de razões trigonométricas é estendido a qualquer ângulo α.

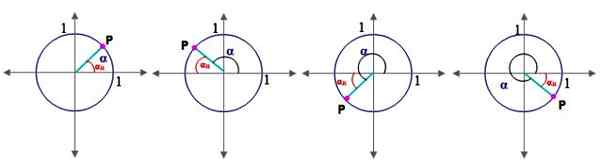Figura 2.- Ângulos nos quadrantes e o ângulo de referência no círculo unitário. Fonte: f. Zapata.

Para isso, é necessário definir o conceito de ângulo de referência α primeiro_R:

Pode atendê -lo: conjunto finito: propriedades, exemplos, exercícios resolvidos

Ângulo de referência

Seja α um ângulo na posição padrão (aquele cujo Lado inicial coincide com o eixo x positivo), seu ângulo de referência α_R Está entre os seus Lado do terminal e o eixo x. A Figura 2 mostra o ângulo de referência para ângulos em quadrante I, II, III e IV.

Para cada quadrante, o ângulo de referência é calculado da seguinte forma:

-Primeiro quadrante: α_R = α

-Segundo quadrante: α_R = 180º - α

-Terceiro quadrante: α_R = α - 180º

-Quarto quadrante: α_R = 360º - α

Observe que o primeiro ângulo de quadrante α coincide com seu ângulo de referência. Bem, as razões trigonométricas para o ângulo α são as mesmas que seu ângulo de referência, com os sinais de acordo com aqueles que têm os quadrantes nos quais o lado terminal de α cai.

Em outras palavras, as razões trigonométricas cosseno e mama do ângulo α coincidem com as coordenadas do ponto P, de acordo com a Figura 2.

Na figura seguinte, vemos as razões trigonométricas de alguns ângulos notáveis, deduzidos do círculo unitário.

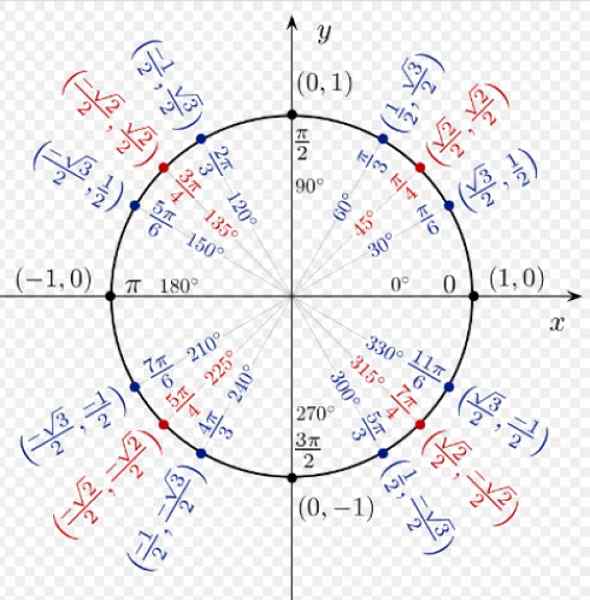Figura 3. Coordenadas de alguns pontos notáveis ​​no círculo unitário. Fonte: Wikimedia Commons.

As razões pelas quais Coseno e o peito de qualquer ângulo no quadrante i são todos positivos. Para α = 60º, temos as coordenadas (1/2; √3/2), que correspondem, respectivamente, a COS 60º e sen 60º.

As coordenadas de α = 120º são (-1/2; √3/2), pois estão no segundo quadrante, a coordenada x é negativa.

Layout dos gráficos de cosseno e seio

Com a ajuda do círculo unitário e as coordenadas dos pontos P, é possível desenhar os gráficos das funções cos t e sen t, como veremos abaixo.

Pode atendê -lo: deslocamento angular

Para isso, várias posições do ponto P (t) estão localizadas no círculo unitário. Começaremos com o gráfico da função f (t) = sen t.

Podemos observar que, quando passarmos de t = 0 a t = π/2 (90º), o valor de sen t aumenta para 1, que é o valor máximo.

Por outro lado, de t = π/2 a t = 3π/2, o valor do pecado t diminui de 1, passando por 0 em t = π para o seu mínimo de -1 em t = 3π/2.

A figura mostra o gráfico do primeiro ciclo de f (t) = sen t que corresponde ao primeiro retorno ao círculo unitário, essa função é o período periódico 2π.

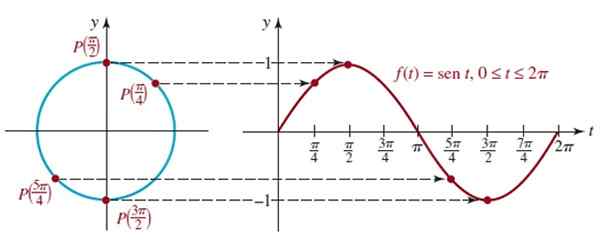Figura 4. Figura do gráfico de f (t) = sen t para um ciclo. Fonte: Zill, D. Álgebra, trigonometria e geometria analítica.

Um procedimento análogo pode ser realizado para obter o gráfico da função f (t) = cos t, como mostrado na seguinte animação:

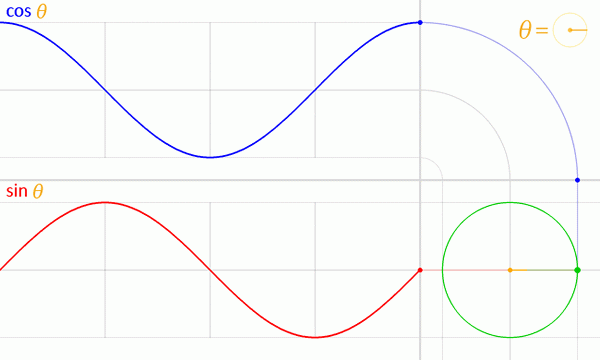Figura 5. Gráficos do seno e cosseno funções do círculo unitário. Fonte: Wikimedia Commons.

Propriedades de funções de Seno e Coseno

-Ambas as funções são contínuas no conjunto de números reais e também periódicos, do período 2π.

-O domínio das funções f (t) = sen t e f (t) = cos t são todos números reais: (-∞, ∞).

-Para a rota mamária ou sinusal e cosseno, você tem o intervalo [-1,1]. Os colchetes indicam que -1 e 1 estão incluídos.

- Os zeros do sin são os valores que correspondem a nπ com n inteiro, enquanto os zeros de cos t são [(2n+1)/2] com n também inteiro.

-A função f (t) = sin t é ímpar, tem simetria em relação à origem enquanto a função COS T é uniforme, sua simetria é em relação ao eixo vertical.

Pode atendê -lo: seleções aleatórias com ou sem substituição

Exercícios resolvidos

- Exercício 1

Dado cos t = - 2/5, que é a coordenada horizontal do ponto P (t) no círculo unitário no segundo quadrante, obtenha a coordenada vertical correspondente sen t.

Solução

Como P (t) pertence ao círculo unitário, no qual é cumprido que:

x² + e² = 1

Portanto:

y = ± √ 1 - x²

Como P (t) está no segundo quadrante, o valor positivo será tomado. A coordenada vertical do ponto P (t) é y:

y = √ 1 - (-2/5)² = √0.84

- Exercício 2

Um modelo matemático para temperatura T Em graus Fahrenheit em qualquer dia, t Horas após a meia -noite, é dado por:

T (t) = 50 + 10 sen [(π /12) × (t - 8)]

Com T entendeu entre 0 e 24 horas. Encontrar:

a) A temperatura às 8h.

b) Horas durante as quais t (t) = 60 ºf

c) temperaturas máximas e mínimas.

Solução para

Substituímos t = 8 na função dada:

T (8) = 50 + 10 sen [(π/12) × (t-8)] = 50 + 10 sen [(π/12) × (8-8)] =

= 50 + 10 x sen 0 = 50 ºf

Solução b

50 + 10 sen [(π/12) × (t-8)] = 60

É uma equação trigonométrica e você deve limpar o desconhecido "T":

10 sen [(π/12) × (t -8)] = 60 - 50 = 10

sin [(π/12) × (t-8)] = 1

Sabemos que sen π/2 = 1, portanto, o argumento da mama deve ser 1:

(π/12) × (t-8) = π/2

T-8 = 6

t = 14 h

Conclui -se que 14 horas após a meia -noite a temperatura é de 60 °, ou seja, as 14:00. Não há outra hora ao longo do dia (24 horas) em que isso acontece.

Solução c

A temperatura máxima corresponde ao valor em que sen [(π/12) × (t-8)] = 1 e é 60 ºF. Por outro lado, o mínimo ocorre se sen [(π/12) × (t -8)] = -1 e for 40 ºf.

Referências

1. Figuera, j. 1999. Matemática. 1º. Diversificado. Edições Bolivarianas Collegiate.
2. Hoffman, J. Seleção de questões de matemática. Volume 4.
3. Jiménez, r. 2008. Álgebra. Prentice Hall.
4. A matemática é divertida. Círculo unitário. Recuperado de: De: Mathsisfun.com.
5. Wikipedia. Identidades e fórmulas de trigonometria. Recuperado de: é.Wikipedia.org.
6. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.