História do pano de fundo e geometria de desenvolvimento de sua origem

O História da geometria Começa com as primeiras civilizações que fizeram uso desse ramo da matemática de maneira prática, especificamente os povos do vale indo e Babilônia que conheciam os triângulos obtusos, cerca de 3000 para.C.

Nos escritos do escriba egípcio Ahmes (1550 para.C.) Os métodos são usados ​​para calcular a área de um círculo. Por sua parte, os babilônios tinham regras gerais para medir volumes e áreas. 

Ahme Papyrus ou Rhind Mathematics Papyrus

Ambas as civilizações, os egípcios e os babilônios, conheciam versões do teorema de Pitágoras 1500 anos antes das versões pitagóricas. Por outro lado, os índios do período védico (1500-100 para.C.) usou geometria na construção de altares.

[TOC]

Grécia Antiga

Os gregos estavam inclinados para o desenvolvimento da matemática por um longo tempo. Personagens como Pitágoras e Platão, relacionados a números com tudo o que existe no mundo. Para eles, a matemática foi a chave para interpretar o universo; Este ideal seguiu os seguidores dos pitagóricos por vários séculos.

Contos de Miletus

Tales de Mileto foi um dos primeiros gregos a contribuir para os avanços da geometria. Um longo tempo gasto no Egito e com esses conhecimentos básicos aprendidos. Ele foi o primeiro a estabelecer fórmulas de medição de geometria.

Contos de Miletus

Ele conseguiu medir a altura das pirâmides do Egito, medindo sua sombra no momento exato em que sua altura era igual à medida de sua sombra.

Pitágoras

Pitágoras

Dentro da contribuição mais significativa de Pitágoras (569 para.C. - 475 a.C.) Para a geometria é o famoso teorema de Pitágoras, que estabelece que dentro de um triângulo retângulo o quadrado da hipotenusa (o lado oposto ao ângulo reto) é igual à soma dos quadrados dos lados restantes.

Elementos de Euclides

O trabalho mais proeminente que foi resgatado desde os tempos antigos tem sido o estudo Os elementos, de Euclid de Alejandría (325 a.C. - 265 a.C.), feito durante os anos 300 para.C. É um trabalho de grande valor histórico que serviu de base para o ensino de matemática por mais de 2000 anos.

Euclides

Os elementos Foi um dos primeiros livros e compilações de estudos que explicaram princípios matemáticos que poderiam ser aplicados a qualquer situação. Inclui postulados, que são os princípios fundamentais da geometria em seu trabalho. Por outro lado, existem os princípios quantitativos conhecidos como noções básicas.

O ensino de euclides reduziu os instrumentos de construção na geometria para apenas dois: uma regra sem medidas e uma bússola. Isso gerou os três problemas clássicos que não encontraram respostas até o século XIX: a quadratura do círculo, a duplicação do cubo e a triseção de um ângulo. 

Pode servir a você: em que século os espanhóis conquistaram Tenochtitlán?

Para os antigos, as duas entidades geométricas ideais eram a linha reta e o círculo; portanto, a maioria dos teoremas geométricos propostos foram o produto da exploração com esses instrumentos.

Geometria em astronomia

A geometria também estava se beneficiando para os gregos em termos de estudo das estrelas. Eles calcularam os movimentos através da observação e fizeram planos geométricos do céu estabelecendo a terra como um ponto central, e tanto o sol quanto a lua e os outros planetas e entidades que se moviam ao redor deles, girando em um conjunto de círculos. 

Uma das contribuições mais influentes foi o Almagest, escrito no segundo século d.C de Claudio Ptolomeu (100 D. C.- 170 d.C), um contêiner de tratado astronômico das estrelas. Foi o texto mais completo de seu tempo e influenciou os estudos astronômicos de maneira transcendental até a Idade Média muito avançada. Fazia parte da mídia que mais popularizou o sistema geocêntrico, que alegou que a Terra era o centro do universo.

Ptolomeu

Influência islâmica

Nos séculos de IX, quando o mundo árabe estava em sua grande expansão, grande parte de sua cultura permeava várias áreas da ciência e das artes. Eles eram grandes fãs das obras matemáticas e filosóficas dos gregos. 

Um dos ramos mais explorados em suas necessidades foi a astronomia, a fim de localizar a orientação exata na qual Meca era executar as frases.

Seguindo os estudos de Euclides e outras contribuições, como as de Ptolomeu, os muçulmanos desenvolveram a projeção estereográfica, ou seja, a projeção da esfera celestial no plano para usá -lo como um mapa. Isso significava progresso em relação ao estudo da trigonometria.

Entre os personagens mais representativos está Thābit Ibn Qurra (826/36-901) que fez traduções relevantes dos textos antigos de Apollonius, Arquimedes, Euclides e Ptolomeu. Alguns deles são as únicas versões sobreviventes dos escritos antigos.

As explorações sobre geometria astronômica também permitiram a criação de um dos instrumentos mais representativos, o Astrolabio, que simplificou os cálculos astronômicos do momento. Além disso, este instrumento também lhes permitiu conhecer o tempo e finalmente obter a orientação para Meca. 

Pode servir a você: 8 costumes e tradições dos mixtecs

Desenvolvimento Legado Europeu

No século XII, após a inserção dos ensinamentos clássicos dos gregos, graças à expansão muçulmana e ao desenvolvimento de suas mesmas descobertas, as traduções dos textos latinos diretamente do grego começaram a ser feitos diretamente do grego ou da língua árabe. 

Isso daria caminho para um novo aprendizado na Europa que seria promovido pelo Renascença. A redescoberta de noções como a "evidência" começou, um conceito desenvolvido entre os gregos interessados ​​na demonstração dos postulados na realidade.

Geometria em Art

O conhecimento também se refletiu nas artes, como pintura ou arquitetura, uma vez que a geometria começaria a ser uma parte fundamental do desenvolvimento da perspectiva na arte.

Filippo Brunelleschi (1377-1446), foi quem conseguiu desenvolver a perspectiva linear através da matemática. O objetivo dessa teoria era representar em um plano um espaço tridimensional de como foi percebido pelo olho humano. Assim, estabelece que todas as linhas em uma imagem tiveram que convergir ou encontrar um vazamento para gerar a sensação de profundidade. 

Filippo Brunelleschi. Fonte: I, Sailko/CC BY-S (http: // criativeCommons.Org/licenças/BY-SA/3.0/)

Brunelleschi foi o primeiro a descrever a perspectiva como um procedimento científico e isso funcionou como base dos empregos subsequentes nas artes.

Dentro de outros exemplos da aplicação da geometria ao estudo da arte e do ser humano em si, está obra de Leonardo da Vinci (1452 -1519) em seu desenho O homem de Vitruviio. É um estudo baseado nas proporções mais perfeitas para o corpo humano através de uma análise geométrica de sua estrutura.

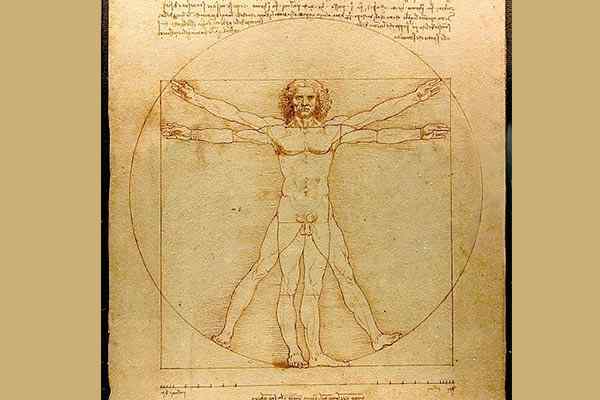O Homem de Showcase de Leonardo da Vinci / Domínio Público

Entre outras áreas, a arquitetura também se destaca, onde vários elementos como simetria e equilíbrio começaram a aparecer como características fundamentais. Portas e janelas retangulares, quadradas, posicionadas de maneira equilibrada; Uso de elementos clássicos da antiguidade, como colunas, cúpulas e cofres.

Passo para a modernidade

A análise de perspectivas e projeções durante o Renascimento foi um dos incentivos para despertar o interesse dos matemáticos. A partir deste momento, bases matemáticas mais sólidas e complexas começam a ser fundadas na geometria.

Um dos trabalhos mais importantes para a modernidade foi o do arquiteto Girard desarmado (1591-1661), que supunha o começo para a geometria projetiva. Por um lado, estabeleceu que as linhas paralelas em uma projeção devem convergir em um ponto da linha infinita, ou seja, o horizonte.

Pode atendê -lo: rebelião tuxtepec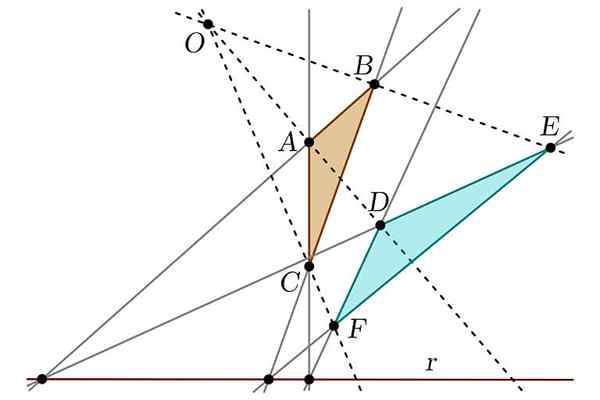Desarrata o teorema

Por outro lado, ele também descobriu o que seria reconhecido como o teorema de Desarranger, que estabelece a relação entre duas figuras que podem ser consideradas "projetivas". Também foi responsável por simplificar as obras de Apollonius em relação às seções de um cone, fazendo analogias entre esta figura e o cilindro.

Outro grande evento do período foi a criação de geometria analítica através dos estudos de René Descartes (1596-1650) e Pierre de Fermat (1601-1665) independentemente. Este é o estudo da geometria através do uso de um sistema de coordenadas. 

René Descartes trabalhando em sua área de trabalho. Wikimedia Commons

Geometria não -euuclidiana

Os estudos do século XVIII e XIX começaram em geometria não -euuclidiana. Especificamente foram Gauss, Johann Boleai e Lobachevsky, que descobriram que o quinto postulado de Euclides, conhecido como postulado paralelo, não podia ser verificado.

Dessa forma, eles desenvolveram um tipo de geometria em que este postulado foi qualificado como falso. Essa nova forma foi bem -sucedida, fornecendo resultados satisfatórios em estilos de geometria que não atendiam necessariamente a todos os postulados euclides. Assim, geometria hiperbólica e geometria elíptica nasceram mais tarde.

Vale a pena destacar o trabalho de Leonhard Euler (1707-1783) no século 18, com relação ao desenvolvimento da notação matemática. Posteriormente, o século XX traria consigo o desenvolvimento de campos mais específicos da geometria, entre os quais são:

-Geometria algébrica: É um ramo da matemática que combina álgebra abstrata e geometria analítica.

-Geometria finita: É um sistema geométrico composto por uma quantidade finita de pontos, ou seja, eles têm um fim ou limite e, portanto, podem ser medidos.

-Geometria Digital: É um ramo da ciência da computação que o estudo de algoritmos e estruturas de dados que podem ser representadas em termos geométricos. 

Referências

1. (2016) O que fez de elementos Euclides o único livro que pode competir com a Bíblia. BBC. BBC recuperou.com
2. Os três problemas clássicos da matemática grega. Universidade de Antioquia. Recuperado do ensino.você.Edu.co
3. Heilbron J.L (2020). Geometria. Encyclopædia britannica. Recuperado da Britannica.com
4. História da geometria. Wikipédia, a enciclopédia livre. Recuperado de.Wikipedia.org
5. Geometria analítica. Wikipédia, a enciclopédia livre. Recuperado de.Wikipedia.org
6. (2017) Geometria e Matemática no Renascença. Recuperado dos uksays.com
7. Sáiz a. Perspectiva linear em Brunelleschi. Universidade de Valencia. UV recuperado.é
8. Os editores da Encyclopaedia Britannica (2019). Arquitetura renascentista. Encyclopædia britannica. Recuperado da Britannica.com
9. Andersen K (2020). Girard desarmado. Encyclopædia britannica. Recuperado da Britannica.com
10. (2011) Uma introdução interessante à geometria computacional. Recuperado dos gaussianos.com