Matemática

Homotecia negativa

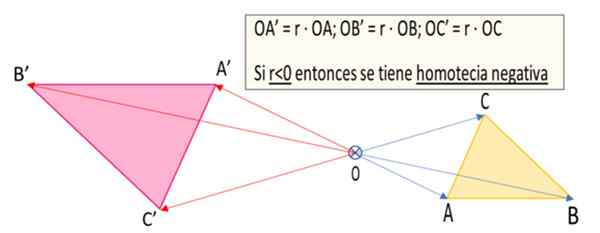
figura 1. O triângulo a'b'c 'é a transformação homotética do triângulo ABC em relação ao ponto ou com um motivo de homotecia negativa r = -1.5 (preparado por: f zapata).

O que é homotecia negativa?

A homotecia negativa é uma transformação na qual um polígono contido em um plano tem como imagem outro polígono no mesmo plano, de ângulos iguais e com os lados correspondentes proporcionais aos do original. Quando homotecia é negativo, a imagem é girada meia curva em relação à figura inicial.

Homotecia é caracterizada por ter um centro de homotecia QUALQUER e uma constante de proporcionalidade chamada Razão r. Quando r É um número negativo, então se fala de homotecia negativa.

Como é feita uma transformação de homotecia?

Para explicar como uma homotecia negativa é realizada, levaremos o caso da Figura 1 em que um triângulo é abc quem quer construir seu homotético negativo.

1.- Começa a escolher um centro de homotecia, que é esse caso é o ponto QUALQUER.

2.- A partir de QUALQUER Segmentos orientados são construídos (vetores) OA, Ob e Oc que vão do centro da homotecia para cada um dos vértices do triângulo.

3.- Uma razão homotecia é escolhida r. Como você quer uma homotecia negativa, então r Deve ser menor que zero. No caso da Figura 1, foi tomado R = -1.5.

4.- Os vetores são desenhados Oa ', Ob ' e Oc ', quais são respectivamente Oa '= r ∙ OA, Ob '= r ∙ Ob e Oc '= r ∙ OC. Como R = -1.5, Esse é um número negativo, depois os vetores Oa ', Ob ' e Oc ' Eles têm direção contrária aos seus colegas correspondentes, ou seja, OA, Ob e Oc. Mas como o valor absoluto da razão r é | R | = 1.5 os tamanhos de Oa ', Ob' e Oc ' Eles são uma vez e meio mais do que os de seus colegas OA, Ob e Oc.

5.- As pontas dos vetores Oa ', Ob ' e Oc ' Defina os vértices do triângulo A'b'c ' Qual é o homotético negativo do triângulo abc.

Propriedades de homotecia negativa

O homotecia negativa, também chamado Homotecia inversa, Tem as seguintes propriedades:

Pode atendê -lo: múltiplos de 8: o que são e explicação

1.- Os lados correspondentes entre o polígono da imagem e o polígono original têm comprimentos proporcionais, sendo a constante da proporcionalidade o valor absoluto da razão homotecia, ou seja, a imagem é amplificada em um fator | r | sempre que | r | é maior que a unidade, mas a imagem é reduzida se | r | é menor que a unidade.

2.- Os ângulos entre os lados correspondentes da imagem e a figura original têm as mesmas medidas.

3.- Os lados homólogos entre o original e a imagem são paralelos um ao outro.

4.- Os segmentos correspondentes no caso de homotecia negativa são paralelos, mas com orientação ou direção oposta. Por exemplo, na Figura 1, o segmento AB tem seu A'B 'paralelo ao primeiro, mas com a direção oposta.

Comparação com homotecia positiva

É chamado de homotecia positiva que na qual a razão homotecia é um número positivo. Para construir uma homotecia positiva, as mesmas etapas são seguidas como as de homotecia negativa:

1.- Escolha um centro de homotecia, no nosso caso o ponto QUALQUER (Veja a Figura 2).

2.- Desenhe os segmentos orientados (vetores), variando do centro de homotecia até os vértices do polígono, no caso da Figura 2 Estes são: OA, Ob e Oc.

3.- Escolha uma relação homotecia que seja um número positivo, por exemplo, no caso da Figura 2, foi escolhido R = 0.5.

4.- Os vetores são desenhados Oa ', Ob ' e Oc ', quais são respectivamente Oa '= r ∙ OA, Ob '= r ∙ Ob e Oc '= r ∙ OC. Como r É um número positivo, depois os vetores Oa ', Ob ' e Oc ' Eles têm o mesmo endereço que OA, Ob e Oc. Os comprimentos de Oa ', Ob' e Oc ' Eles são metade que seus colegas OA, Ob e Oc, já que o motivo é R = 0.5.

5.- Finalmente, os vértices A'b'c 'são unidos para obter o triângulo homotético para ABC com a razão 1/2.

Pode servir a você: quadrilateral: elementos, propriedades, classificação, exemplos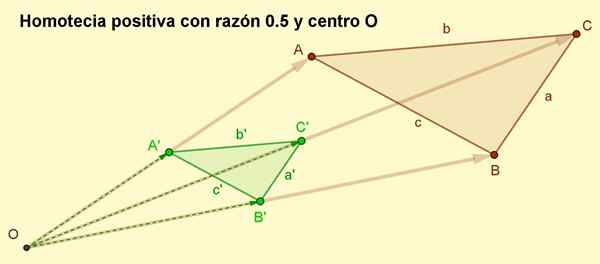

Figura 2. Homotecia positiva, com razão, 0,5 dos resultados do Triângulo ABC. Em homotecia positiva, a orientação é mantida. (Preparado por: f. Zapata)

Exemplos de homotecia

Homotecia aparece em várias situações:

Projetores de cinema

Em um projetor de filme, a imagem gravada em um quadro é projetada e se expande em uma tela, e para que a projeção seja vista à direita, é necessário que o quadro seja investido, uma vez que o centro de homotecia está no centro da lente da Lente da lente do projetor, entre o quadro e a tela (homotecia negativa, veja a Figura 3)

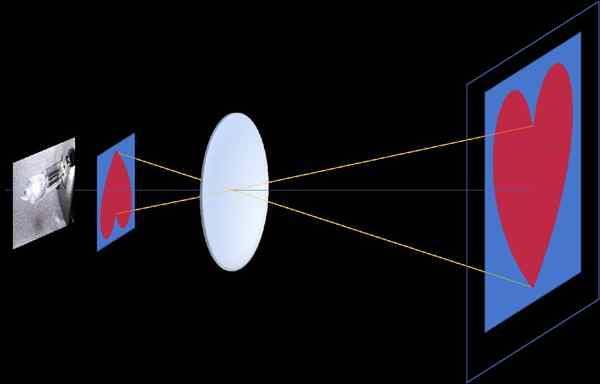Figura 3. Homotecia negativa aparece no projetor do filme, entre a imagem registrada em um quadro translúcido e a imagem projetada na tela. O centro de homotecia fica no centro óptico da lente, por sua vez localizado entre o quadro e a tela. Fonte: f. Zapata.

Câmeras fotográficas

Este principio también aplica a las cámaras fotográficas: la luz proveniente de la imagen ubicada a cierta distancia de la lente se proyecta sobre el sensor fotográfico, el cual puede ser una película química sensible a la luz o un sensor CCD, si se trata de una Câmera digital.

A imagem registrada no sensor é invertida em relação à real e geralmente é proporcionalmente menor que ela.

Aplicação prática

O sol não deve olhar diretamente, porque causa danos permanentes à retina, mas existem duas possibilidades para estudá -lo: use filtros que atenuem a intensidade da luz ou projetem sua imagem em uma tela.

Pode atendê -lo: variação proporcional

Um dispositivo de projeção consiste em um tubo de comprimento d. Uma das extremidades do tubo é coberta com papel alumínio e brocas em seu centro com um alfinete. A outra extremidade, que servirá como tela, é coberta com papel translúcido, que pode ser papel de cebola ou papel albaneno (papel vegetal).

Exercício

Determine o diâmetro do sol, sabendo que o raio orbital terrestre é da ordem de 150 milhões de quilômetros, que o tubo de projeção, como o mostrado na Figura 4, tem 2,2 metros de comprimento e que a imagem projetada é 2, 1 cm de diâmetro.

Figura 4. No tubo para projetar o disco solar, ocorre uma relação homotecia negativa. Fonte: f. Zapata.

Solução

Os dados são os seguintes:

Comprimento do tubo: D = 2,2m
Diâmetro da imagem projetada do Sun: S = 2,1 cm
Distância do tubo solar: r = 150 x 10^9 m
Diâmetro do Sol Real: S = ¿?

Para obter o diâmetro do sol, uma taxa de proporcionalidade é aplicada de acordo com a proporcionalidade da homotecia (ver Figura 4):

A distância ao sol está no comprimento do tubo, pois o diâmetro do sol é para o diâmetro da imagem projetada:

(R / d) = (s / s)

Limpando essa igualdade de que o diâmetro real do sol tem o diâmetro da projeção multiplicado pelo quociente entre a distância do sol e o comprimento do tubo:

S = s (r / d)

Colocar os valores numéricos são:

S = 2,1 x 10^-2 M (150 x 10⁹ m / 2,2 m)

S = 1,43 x 10⁹ m.

Este resultado é interpretado da seguinte forma: o diâmetro real do sol é de 1,43 milhão de quilômetros.

Referências

Álvaro Rendón, para. R. 2004. Desenho técnico: caderno de atividade.
Antonio Álvarez de la Rosa, J. eu. 2002. Afinidade, homologia e homotecia.
Baer, r. 2012. Álgebra linear e geometria projetiva. Couer Corporation.
Hebert, e. 1980. Matemática Geral, Probabilidades e Estatísticas.
Messerve, b. E. 2014. Conceitos fundamentais de geometria. Couer Corporation