Heptágono

Um exemplo de heptagon

O que é um heptagon?

Ele heptágono É um polígono com sete lados e sete ângulos internos. Como uma palavra geométrica, a palavra heptagon se origina do grego Hepta, o que significa sete e Gonos, traduzido como um ângulo. É, portanto, um polígono com sete ângulos.

Um polígono é uma figura geométrica plana que forma e fechando três ou mais segmentos, também chamados lados. Os pontos comuns que os lados têm são chamados Vértices.

A região entre os lados adjacentes, no interior da figura, é o Ângulo interno, cujo vértice também é um dos vértices do heptagon.

Se todos os lados e ângulos internos têm a mesma medida, é um heptagon regular, caso contrário, é a Heptagon irregular. Os heptons irregulares adotam uma grande variedade de formas.

Um heptagon também pode ser convexo qualquer côncavo, De acordo com a medida de seus ângulos internos. Se os ângulos internos medirem menos de 180 °, o heptagon é convexo, mas se um ou mais dos ângulos exceder 180 °, então é côncavo.

Um heptagon cujos lados são todos os mesmos medida Balateral. Isso pode ser côncavo ou convexo, regular ou irregular.

Heptagon regular e irregular

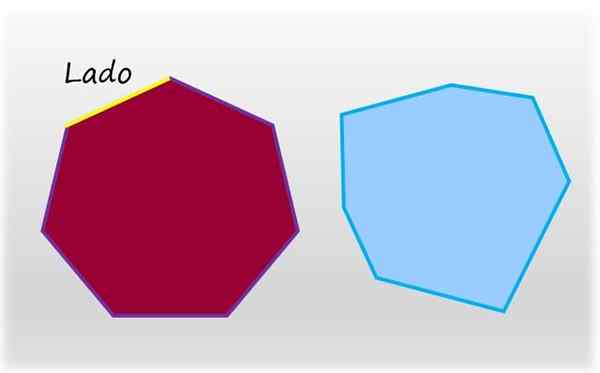O heptagon é a figura plana e fechada de sete lados. À esquerda, um heptagon regular, cujos lados e ângulos internos têm igual medida. À direita, um heptogon irregular. Fonte: f. Zapata.

O heptagon regular é aquele que tem seus sete lados e seus sete ângulos internos de igual medida, o oposto de um heptagon irregular, que tem pelo menos um lado de medida diferente, ou um ângulo interno diferente.

O heptagon regular

Simetria

Um heptagon regular é uma figura altamente simétrica. Os segmentos podem ser desenhados que conectam um vértice ao ponto médio do lado oposto, que se cruzam no centro do heptagon. Estes são os sete eixos de simetria na figura.

Pode servir a você: área de um pentágono regular e irregular: como é tomado, exercícios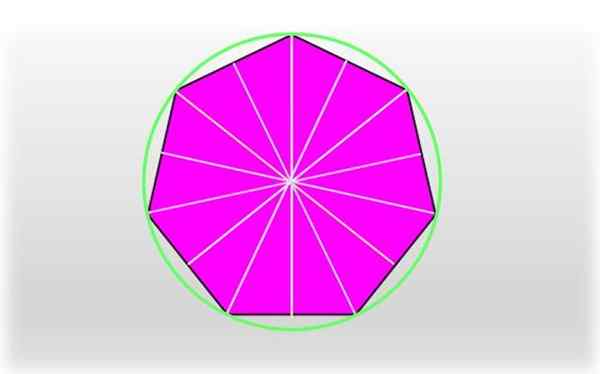 Um heptagon regular e seus eixos de simetria. A circunferência que passa por cada um dos vértices do heptagon é chamada de circunferência circunscrita.

O segmento que se junta a um vértice com o centro do heptagon é chamado Circunradio, Corresponde ao raio da circunferência única que passa por todos e cada um dos vértices, como mostrado na figura.

Ângulos

No heptagon, os seguintes ângulos se destacam:

• Ângulo interno ϕ, cujo vértice coincide com um dos vértices do heptagon, sendo os lados do ângulo, dois dos lados adjacentes do heptagon. Para um heptagon regular, a medida de cada um dos sete ângulos internos é de aproximadamente 128.57 °.
• Ângulo externo, aquele que se forma entre um dos lados e o prolongamento de um dos lados adjacentes, sendo o vértice comum entre esses dois lados, o vértice do ângulo. Da mesma forma, sete ângulos externos são formados e seu valor é calculado subtraindo 180 ° do ângulo interno, que para o heptagon regular, resulta em 51.43 °.
• Ângulo central θ, Tem seu vértice no centro do heptgon regular. É calculado dividindo 360 ° por 7, o que resulta em aproximadamente 51.43 °.

A soma do ângulo interno e o ângulo central é igual a 180 °, ou seja::

ϕ + θ = π

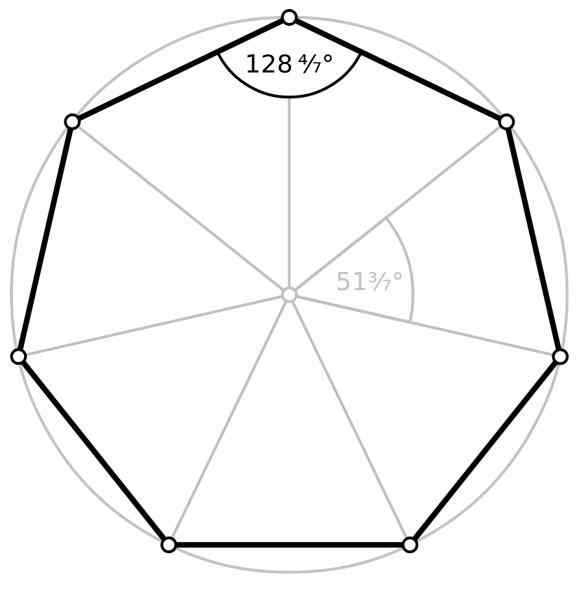Ângulo interno e ângulo central do heptogon regular. Fonte: Wikimedia Commons

Área

Para o heptagon comum, existem fórmulas, enquanto para o heptagon irregular você deve recorrer a outros métodos, como dividi -lo em outros polígonos mais simples, como triângulos.

Pode atendê -lo: Regra T: Características, para que sejam, exemplos

Área regular de heptagon

1. Se o perímetro P e o apoteme para_p:

Seja para a área de heptagon. Há uma fórmula para calcular a área, válida para qualquer polígono regular:

2. Se o L e o apotem são conhecidos para_p:

Como o perímetro é a soma dos lados, e o lado mede L no heptagon regular, é obtido:

P = 7⋅l

Substituindo na fórmula anterior:

3. Se o lado for conhecido        

A seguir, é conhecida uma fórmula aproximada e válida quando a medida do heptagon é conhecida:

A = 3.634 ∙ l²

Área irregular de heptagon

A área irregular de heptagon pode ser calculada por triangulação, que consiste em dividir o heptogon em cinco triângulos (veja a figura a seguir). A área de cada um é calculada e os resultados são adicionados, obtendo assim a área completa do heptagon.

O outro método é chamado Gauss determinante, E é necessário colocar o heptagon em um sistema de coordenadas retangulares, a fim de conhecer as coordenadas de cada vértice. A área é calculada por uma fórmula que envolve os valores dessas coordenadas.

Diagonais

As diagonais São segmentos que conectam um vértice a outro que não é consecutivo (se o segmento conectar dois vértices consecutivos é o lado). Um heptagon tem 14 diagonais no total.

O número de diagonais d de qualquer polígono é calculado através da fórmula:

D = n · (n - 3) / 2

Substituindo n = 7, permanece:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Soma de ângulos internos

Para qualquer heptagon, independentemente de ser regular ou não, a soma de seus ângulos internos é igual a 900 ° ou 5π radianos.

Pode servir a você: Razões trigonométricas: exemplos, exercícios e aplicações

Esta propriedade é muito fácil de demonstrar, pois isso o heptagon é dividido em triângulos individuais que não se sobrepõem, desenhando segmentos retilíneos que unem os vértices, sem se cruzar.

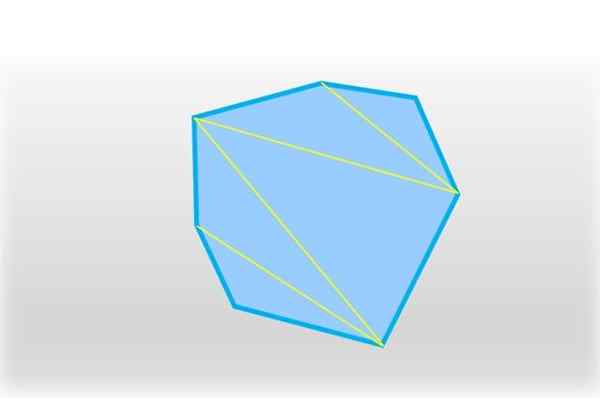Um heptagon pode ser dividido em cinco triângulos, juntando -se por um segmento dois vértices não consecutivos. Fonte: f. Zapata.

Cinco triângulos são obtidos e, em cada um, a soma de seus ângulos internos é de 180 °, que multiplicada por 5 é igual a 900 °:

5 x 180 ° = 900 °

Fórmulas

Perímetro

Para um heptagon regular de L, o perímetro P é calculado da seguinte forma:

P = 7⋅l

Se o perímetro for irregular, os comprimentos de cada um dos sete lados são adicionados.

Medida de ângulo interno

Em um heptagon regular, o ângulo interno θ mede:

θ = [180 (n-2)]/n

Onde n = 7.

Apótema

Seja o lado do heptogon comum. O apotem é o segmento que vai do centro do heptagon, perpendicularmente para o lado oposto.

Deixe um_p A duração do apoteme. Conhecendo o raio da circunferência circunscrita, que é indicada como r_c E o lado l do heptagon, você tem:

Conhecendo o ângulo interno θ, o acima é equivalente a:

Área

Se é um heptagon regular de L, a área A é dada por:

A = 3.634 ∙ l²

Quando o heptagon é irregular, são necessárias as coordenadas retangulares de cada vértice, dada por (x_n , e_n), Onde n = 1, 2, 3 ... 7.

Então a fórmula a seguir é aplicada para encontrar a área A:

Diagonais

O número d de diagonais é dado por:

D = n · (n - 3) / 2

Onde n = 7 para o heptagon.

Como fazer um heptagon

A animação a seguir mostra como desenhar aproximadamente um heptagon regular, usando regra e bússola.

Construção do heptagon regular. Fonte: Wikimedia Commons

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Lemonis, m. Calculadora Hepalle regular. Recuperado de: Calcresource.com.
3. Math Open Reference. Área de Polígono. Recuperado de: MathpenRef.com.
4. Fórmulas do Universo. Heptágono. Recuperado de: universoformulas.com.
5. Wikipedia. Heptágono. Recuperado de: é.Wikipedia.com.