Funções trigonométricas inversas, derivadas, exemplos, exercícios

As Funções trigonométricas inversas, Como o nome indica, eles são as funções inversas correspondentes do seio, cosseno, tangente, cotangente, secagem e funções de colheitadeira.

As funções trigonométricas inversas são denotadas pelo mesmo nome de sua função trigonométrica direta correspondente, mais o prefixo ARCO. Desta forma:

1.- Arcsen (x) É a função trigonométrica inversa da função pecado (x)

2.- Arccos (x) É a função trigonométrica inversa da função cos (x)

3.- Arctan (x) É a função trigonométrica inversa da função Bronzeado (x)

4.- Arccot ​​(x) É a função trigonométrica inversa da função berço (x)

5.- Arcsec (x) É a função trigonométrica inversa da função sec (x)

6.- ArcCSC (x) É a função trigonométrica inversa da função CSC (x)

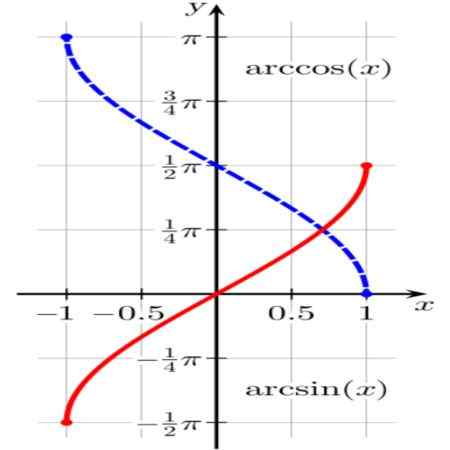
figura 1. Funções de Arcsen (x) (em vermelho) e Arccos (x) (em azul). Fonte: Wikimedia Commons.

A função θ = Arcsen (x) Resulta em um arco de unidade θ (ou ângulo em Radianes θ) tal que sin (θ) = x.

Assim, por exemplo, Arcsen (√3/2) = π/3 Como é conhecido, o peito de π/3 radianos é igual a √3/2.

[TOC]

Valor principal das funções trigonométricas inversas

Para que uma função matemática f (x) tenha G (x) = F^-1(x) É necessário que essa função seja Injetivo, O que significa que cada valor e o conjunto de chegada da função f (x) vem de um e apenas um valor X.

É claro que esse requisito não é atendido por nenhuma função trigonométrica. Para esclarecer o ponto, vamos perceber que o valor y = 0,5 pode ser obtido a partir da função sinusal das seguintes maneiras:

• sin (π/6) = 0,5
• sin (5π/6) = 0,5
• sin (7π/6) = 0,5

E muito mais, já que a função sinusal é periódica com o período 2π.

Pode atendê -lo: múltiplos de 8: o que são e explicação

Para definir funções trigonométricas inversas, é necessário restringir o domínio de suas funções trigonométricas diretas correspondentes, para que eles atendam ao requisito de injetividade.

Este domínio restrito de função direta será o principal intervalo ou ramo de sua função inversa correspondente.

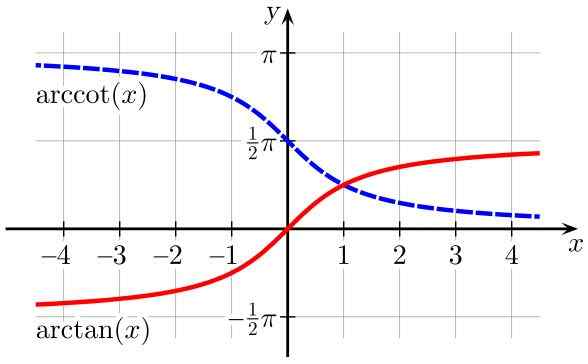Figura 2. Funções de arctan (x) (em vermelho) e arccot ​​(x) (em azul). Fonte: Wikimedia Commons.

Tabela de domínios e faixas de funções trigonométricas inversas

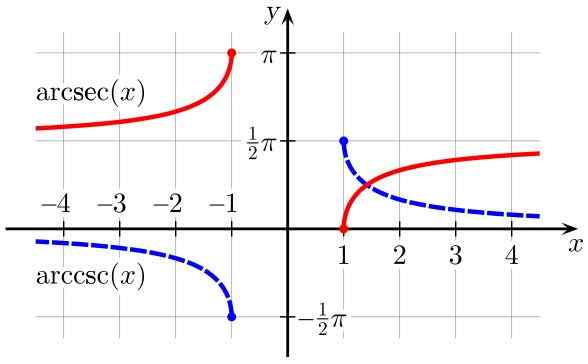Figura 3. Funções ArcSec (X) (em vermelho) e ArcCSC (x) (em azul) (em azul). Fonte: Wikimedia Commons.

Derivado de funções trigonométricas inversas

Para obter os derivados das funções trigonométricas inversas, as propriedades dos derivadas são aplicadas, em particular a derivada de uma função inversa.

Se denotarmos para f (y) à função e por f^-1(x) Para sua função inversa, então o derivado da função reversa está relacionado à derivada da função direta através do seguinte relacionamento:

[F^-1(x)] '= 1/ f' [f^-1(x)]

Por exemplo: se x = f (y) = √y é a função direta, seu inverso será

y = f^-1(x) = x². Vamos aplicar a regra do derivado reverso a este caso simples para ver que esta regra é cumprida:

[x²] '= 1 / [√y]' = 1 / (½ e^-½ = 2 e^½ = 2 (x²)^½ = 2x 

Bem, podemos avaliar esse truque para encontrar aqueles derivados de funções trigonométricas inversas.

Por exemplo, nós tomamos θ = Arcsen (x) Como a função direta, então sua função inversa será sin (θ) = x.

[Arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) =…

… = 1 / √ (1 - x²) .

Dessa forma, todos os derivados das funções trigonométricas inversas podem ser obtidas, que são mostradas abaixo:

Figura 4. Tabela daqueles derivados de funções trigonométricas inversas. Fonte: Wikimedia Commons.

Esses derivados são válidos para qualquer argumento z pertencente a números complexos e, portanto, também são válidos para qualquer argumento real x, pois z = x + 0i.

Pode servir a você: quadrilateral: elementos, propriedades, classificação, exemplos

Exemplos

- Exemplo 1

Encontre Arctan (1).

Solução

O Arctan (1) é o arco da unidade (ângulo em Radianes) ፀ, de modo que o bronzeado (ፀ) = 1. Esse ângulo é ፀ = π/4 porque (π/4) = 1. Então Arctan (1) = π/4.

- Exemplo 2

Calcule Arcsen (cos (π/3)).

Solução

O ângulo π/3 radianos é um ângulo notável cujo cosseno é ½, para que o problema seja reduzido a encontrar Arcsen (½).

Então, trata -se de encontrar o ângulo cujo seno dá ½. Esse ângulo é π/6, já que sen (π/6) = sen (30º) = ½. Portanto, Arcsen (cos (π/3)) = π/6. 

Exercícios

- Exercício 1

Encontre o resultado da seguinte expressão:

Sec (Arcan (3)) + CSC (ArcCot (4))

Solução

Começamos a nomear α = Arcan (3) e β = Arcot (4). Portanto, a expressão que temos que calcular é assim:

Sec (α) + CSC (β)

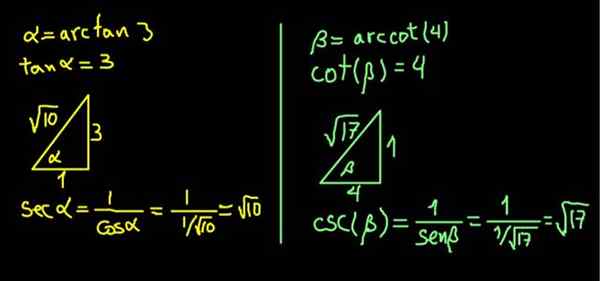
A expressão α = Arcan (3) é equivalente a dizer isso (α) = 3.

Como a tangente é a perna oposta no adjacente, um triângulo retângulo de cateto oposto a α de 3 unidades e uma categoria adjacente de 1 unidade é construída, de modo que assim (α) = 3/1 = 3.

Em um triângulo retângulo, a hipotenusa é determinada pelo teorema de Pitágoras. Com esses valores, é √10, de modo que:

sec (α) = hipotenusa / cateto adjacente = √10 / 1 = √10.

Da mesma forma, β = arcot (4) é equivalente a declarar que o COT (β) = 4.

Um triângulo retângulo de cateto adjacente a β de 4 unidades e um cateto oposto de 1 unidade é construído, de modo que o COT (β) = 4/1.

O triângulo é concluído imediatamente encontrando sua hipotenusa graças ao teorema de Pitágoras. Nesse caso, acabou ter √17 unidades. Então o csc (β) = hipotenusa / cateto oposto = √17 / 1 = √17 é calculado.

Pode atendê -lo: y = 3sen (4x) Período de função

Lembrando que a expressão que devemos calcular é: 

Sec (Arcan (3)) + CSC (Arcot (4)) = Sec (α) + CSC (β) =…

… = √10 + √17 = 3,16 + 4,12 = 7,28.

- Exercício 2

Encontre as soluções de:

Cos (2x) = 1 - sen (x)

Solução

É necessário que todas as funções trigonométricas sejam expressas no mesmo argumento ou ângulo. Usaremos a identidade do ângulo duplo:

Cos (2x) = 1 - 2 sen²(x)

Então a expressão original é reduzida para:

1 - 2 sen²(x) = 1 - sin x x

Uma vez simplificado e fatorizado, ele é expresso como:

sin (x) (2 sen (x) - 1) = 0

Que dá origem a duas equações possíveis: sin (x) = 0 com solução x = 0 e outra equação sen (x) = ½ com x = π/6 como uma solução.

As soluções para a equação levantadas são: x = 0 ou x = π/6.

- Exercício 3

Encontre as soluções da seguinte equação trigonométrica:

cos (x) = pecado²(x)

Solução

Para resolver essa equação, é conveniente colocar um único tipo de função trigonométrica, por isso usaremos a identidade trigonométrica fundamental para que a equação original seja retirada da seguinte maneira:

cos (x) = 1 - cos²(x)

Se nomearmos y = cos (x), a expressão pode ser reescrita como:

e² + e - 1 = 0

É uma equação de segundo grau em e, cujas soluções são:

y = (-1 ± √5) / 2

Então os valores de x que cumprem a equação original são:

x = Arcos ((-1 ± √5) / 2)

A solução real é o sinal positivo x = 0,9046 rad = 51,83º.

A outra solução é complexa: x = (π - 1,06 i) rad.

Referências

1. Hazewinkel, m. 1994. Enciclopédia de Matemática. Kluwer Academic Publishers / Springer Science & Business Media. 
2. Mobile Mate. Funções trigonométricas inversas. Recuperado de: Matemovil.com
3. Fórmulas do Universo. Funções trigonométricas inversas. Recuperado de: universoformulas.com
4. Weisstein, Eric W. Inventar funções trigonométricas. Recuperado de: Mathworld.Volfrâmio.com
5. Wikipedia. Inventar funções trigonométricas. Recuperado de: em.Wikipedia.com