Fórmula e equações de erro aleatório, cálculo, exemplos, exercícios

Ele erro aleatório de uma quantia física consiste nas variações não preditáveis ​​da medida dessa quantidade. Essas variações podem ser produzidas pelo fenômeno que é medido, pelo instrumento de medição ou pelo próprio observador.

Esse erro não se deve ao fato de que algo foi feito errado durante o experimento, mas que é um erro inerente ao processo de medição ou no fenômeno estudado. Isso causa a medida medida às vezes um pouco maior e às vezes um pouco menor, mas geralmente oscila em torno de um valor central.

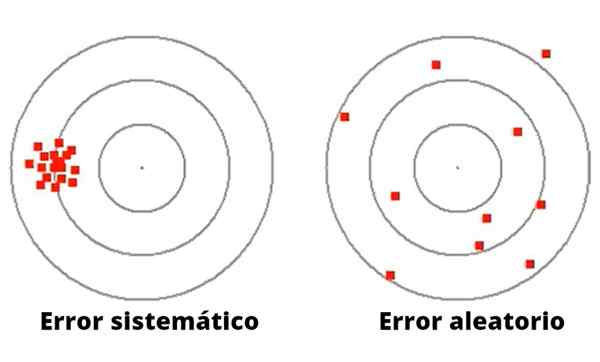
Figura 1- Erros aleatórios variam em magnitude e direção. Pelo contrário, erros sistemáticos tendem a ser consistentes.

Ao contrário do erro aleatório, o erro sistemático pode ser causado por má calibração ou um fator de escala inadequado no instrumento de medição, incluindo uma falha no equipamento experimental ou uma observação inadequada, o que causa um desvio no mesmo sentido.

A Figura 1 ilustra a diferença entre erro sistemático e aleatório no jogo de lançamento do DART para um alvo com círculos.

No caso da esquerda, os dardos estão concentrados em torno de um muito longe do centro. O arremessador desses dardos, embora de bom objetivo, tem uma falha sistemática, talvez de origem visual, ou na forma de jogar.

Por outro.

[TOC]

Fórmulas e equações com erro aleatório

Quando o processo de medição mostra erro aleatório, é necessário.

Obviamente, em cada medição, é necessário tomar cuidado para que as condições em que sejam realizadas sejam sempre iguais.

Pode atendê -lo: Lei de Faraday: fórmula, unidades, experimentos, exercícios,

Suponha que a medição seja repetida n vezes. Como há erro aleatório em cada medição, haverá um valor ligeiramente diferente. Suponha que o conjunto de n Medidas é:

x₁, x₂, x₃,…, X_n

Então, que relatório de valor para medida? 

Valor médio e desvio padrão

O valor médio qualquer média do conjunto de medidas, pelas quais denotamos e é calculado da seguinte forma:

= (x₁ + x₂ + x₃ +… +X_n) / n

Desvio padrão

No entanto, esse resultado tem uma margem de erro dada pelo desvio padrão. Para defini -lo, você deve primeiro conhecer o desvio e depois a variação:

-O desvio d_Yo  que cada valor medido tem XI Em relação ao valor médio é:

d_Yo = x_Yo -

Se a média dos desvios fosse calculada, seria sistematicamente obtida = 0, já que: 

= (d₁ + d₂ + d₃ +… +D_n) /n =

= [x₁ - ) + (x₂ - ) +… +(X_n - )]/n

= (x₁+ x₂ +… + X_n) / n - n / n = - = 0

-A média dos desvios não é útil para conhecer a dispersão das medidas. Por outro lado, o valor médio do quadrado de desvios ou variação, denotado por σ², sim é.

É calculado de acordo com a seguinte fórmula:

σ² = (d₁² + d₂² +.. .+ d_n² ) / (N -1)

Nas estatísticas, esse valor é chamado variação.  

E na raiz quadrada da variação é conhecida como Desvio padrão σ:

σ = √ [(D₁² + d₂² +.. .+ d_n² ) / (n -1)] 

O desvio padrão σ indica que:

1.- 68% das medições feitas estão incluídas no intervalo [ - σ, + σ]. 

2.- 95% das medições estão no intervalo [ - 2σ, + 2σ].

3.- 99,7% das medidas tomadas estão no intervalo [ - 3σ, + 3σ].

Como calcular o erro aleatório?

O resultado da medição é o valor médio das n Medidas denotadas e calculadas de acordo com a seguinte fórmula:

Pode servir a você: velocidade areolar: como é calculado e resolvido exercícios

= (∑x_Yo) / n

No entanto, não é o valor "exato" da medição, pois é afetado pelo erro aleatório ε, que é calculado assim:

ε = σ / √n

Onde:

σ = √ [(∑ (xi -)² ) / (n -1)]

O resultado final da medição deve ser relatado de qualquer uma das seguintes maneiras:

1. ± σ / √n = ± ε Com um nível de confiança de 68%.
2. ± 2σ / √n = ± 2ε Com um nível de confiança de 95%.
3. ± 3σ / √n = ± 3ε Com um nível de confiança de 99,7%.

O erro aleatório afeta o último número significativo da medição, que geralmente coincide com a apreciação do instrumento de medição. No entanto, se o erro aleatório for muito grande, os dois últimos dígitos significativos poderão ser afetados pela variação.

Exemplos de erros aleatórios

Erros aleatórios podem aparecer em vários casos em que uma medida é feita:

Medindo um comprimento com uma fita ou regra

Quando um comprimento é medido com uma regra ou uma fita métrica e as leituras se enquadram entre as marcas da escala, esse valor intermediário é estimado.

Às vezes, a estimativa tem excesso e outro defeito, então o erro aleatório está sendo introduzido no processo de medição.

Figura 2. Erros aleatórios podem aparecer quando um comprimento é medido com uma fita adesiva. Fonte: Pikrepo.

A velocidade do vento

Na medição da velocidade do vento, pode haver mudanças na leitura de um momento para outro, devido à natureza mutável do fenômeno.

Ao ler o volume em um cilindro graduado

Quando o volume é lido com um cilindro graduado, até tentando minimizar o erro de paralela, toda vez que é medido, o ângulo de observação meniscal muda um pouco, e é por isso que as medidas são afetadas por erro aleatório.

Pode servir a você: Primeiro Equilíbrio Condição: Explicação, Exemplos, Exercícios Figura 3.- No laboratório de química, é possível cometer erros aleatórios na leitura de um cilindro de pós -graduação. Fonte: pexels.

Quando a estatura de uma criança é medida

Ao medir a altura de uma criança, especialmente se estiver um pouco inquieto, faz pequenas mudanças de postura mudam levemente a leitura.

Ao usar a escala do banheiro

Quando queremos medir nosso peso com um banheiro, uma pequena mudança no ponto de suporte, mesmo uma mudança de posição pode afetar aleatoriamente a medição.

Exercício resolvido

Um carrinho de brinquedo pode rolar por uma pista reta e inclinado e medido com um cronômetro do tempo que leva toda a pista. 

A medição é feita 11 vezes, com o cuidado de liberar o carrinho do mesmo lugar, sem dar impulso e manter as correções de inclinação.

O conjunto de resultados obtidos é:

3,12S 3.09S 3.04S 3.04S 3.10S 3.08S 3.05S 3.10S 3.11s 3.06s, 3.03s

Qual é o erro aleatório das medidas?

Figura 4. Tomando o tempo de um Strolle de brinquedo que desce através de um avião inclinado. Fonte: Fanny Zapata.

Solução

Como pode ser visto, os resultados obtidos não são únicos e variam um pouco.

O primeiro é calcular o valor médio de descida, obtendo 3.074545455 segundos.

Não faz sentido manter tantas decimais, uma vez que cada medição tem três números significativos e o segundo decimal de cada medida é incerto, pois está no limite de apreciação do cronômetro; portanto, o resultado é arredondado para dois decimais:

= 3,08 s.

Com a calculadora no modo estatístico, o desvio padrão é σ = 0,03 s E o erro padrão é σ / √11 = 0,01 s. O resultado final é expresso da seguinte maneira:

Tempo de descida 

3,08 s ± 0,01s (com um nível de confiança de 68%)

3,08 s ± 0,02s (com um nível de confiança de 95%)

3,08 s ± 0,03s (com um nível de confiança de 99,7%)

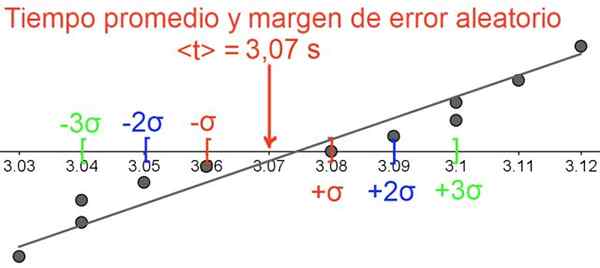Figura 5. A margem de erro aleatória, observe que os dados são agrupados em torno do valor médio. Fonte: f. Zapata.

Referências

1. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
2. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
3. Helmestina a. Erro aleatório vs. Erro sistemático. Recuperado de: pensamento.com
4. Laredo, e. Erros médios. Recuperado de: USB.ir.
5. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.