Função de variável real real e sua representação gráfica

A Função de variável real real Pegue um número pertencente ao conjunto de números reais e o associa a outro valor, também real, por meio de uma regra de correspondência única. Isso significa que o número real obtém, através desta regra, uma imagem única.

As variáveis ​​de partida numérica geralmente são designadas pela letra X, enquanto sua imagem é a letra e. Por outro lado, à regra de correspondência que os vincula também é chamada com outra letra do alfabeto, como a função "f", embora outro possa ser usado.  Na notação compacta, está escrito:

F: x → y = f (x)

figura 1. Gráfico de uma função polinomial real

Para a variável  x é chamado variável independente, enquanto o e É o variável dependente. A função pode ser expressa de várias maneiras, por exemplo, através de uma declaração matemática como estas:

• f (x) = 2x −3
• H (x) = −3x²
• 

Outra forma de expressão é através de um gráfico, o que é muito útil porque permite que você aprecie o comportamento da função de um único olhar. Construir um gráfico é muito simples usando um sistema de coordenadas cartesianas, no qual os pares [x, f (x)] são representados como pontos no plano. Então eles se juntam por uma linha suave e contínua, você pode ver como é a função.

Exemplos

Para construir o gráfico, você pode recorrer a uma tabela de valores nos quais os pontos para o gráfico são colocados. Para os valores variáveis ​​x são selecionados que pertencem ao domínio da função, ou seja, aqueles que, quando substituídos na fórmula, mostram números reais.

Uma vez que os valores de x foram escolhidos, sua imagem y = f (x) é determinada e, dessa maneira, os pares de pontos [x, f (x)] são obtidos que serão gráficos.

Pode servir a você: Função homográfica: Como representar graficamente, exercícios resolvidos

Existem alguns pontos que são importantes e devem ser incluídos na tabela: aqueles em que o gráfico corta os eixos de coordenadas, que se houver, porque nem todas as funções os cruzam.

Para calculá -los, prossiga da seguinte maneira:

-Interseção com o eixo e: x = 0 é feito na fórmula da função e o valor correspondente é calculado.

-Interseção com o eixo x: Y = 0 é feito e a equação f (x) = 0 é resolvida.

Em seguida, o sistema de coordenadas cartesianas é desenhado e cada um dos pontos é plotado, que são então unidos a uma linha suave e contínua, se possível.

Exemplo 1

Construa uma tabela de valores e o gráfico da seguinte função:

f (x) = x² -4

Antes de começar, você precisa encontrar o domínio da função, que é o conjunto de valores reais para os quais a função existe. Como é uma função quadrática, qualquer valor x que pertence aos números reais tem uma imagem real, de acordo com f (x).

Então, a tabela pode ser construída escolhendo qualquer valor x, e o mais simples é começar com as interseções do gráfico com os eixos, se houver. Depois de encontrá -los, outros pontos são procurados para completar a tabela.

Para x = 0

f (0) = -4

Portanto, o primeiro ponto da tabela é (0, -4). Esta é a interseção do gráfico com o eixo e.

Para y = 0

Então y = 0 é feito e a equação que os resultados é resolvida:

x² −4 = 0

x² = 4

As soluções desta equação são: x₁= 2 e x₂= -2. Portanto, existem duas interseções com o eixo x, que são os pontos: (-2,0) e (2.0).

Pode atendê -lo: números perfeitos: como identificá -los e exemplos

Agora você pode encontrar mais pontos para adicionar à tabela de valores:

Para x = 1

f (1) = (1)² - 4 = −3

Para x = - 1

f (−1) = (−1)² - 4 = −3

Para x =  3

f (3) = (3)² - 4 = 5

Para x =  -3

f (−3) = (−3)² - 4 = 5

Tabela de valor

A tabela a seguir mostra os pontos obtidos, que servirão para construir o gráfico de f (x):

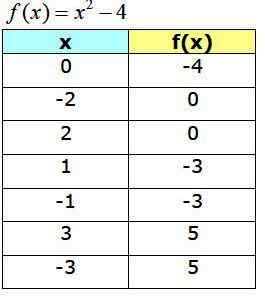Função Gráfico F (x) = X² -4

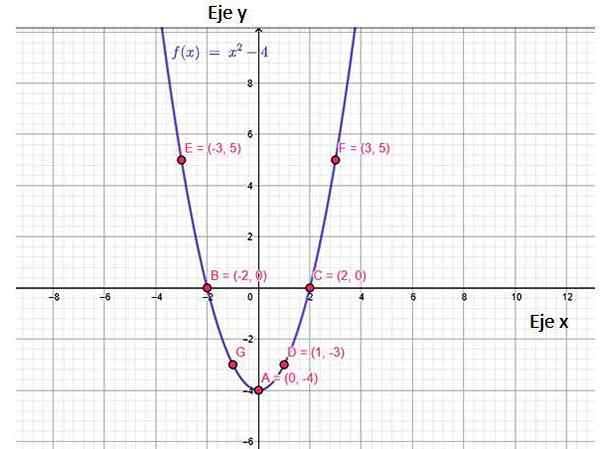Figura 2. Função F (x) Gráfico de função, mostrando alguns pontos que pertencem a ele, incluindo cruzamentos com eixos. Fonte: f. Zapata, através da Geogebra.

O gráfico desta função é uma parábola, que se abre e tem em um ponto mínimo, chamado vértice, de coordenadas (0, −4). É interessante notar que os valores de f (x) começam em y = -4 para ∞. Este é o intervalo da função.

Do gráfico, pode -se concluir que a função é contínua, diminuindo no intervalo (−∞, 0) e aumentando a partir daí.

Exemplo 2

Tendo o gráfico da função, é possível conhecer seu domínio, seu alcance, as interseções que possui com os eixos e visualizar seu comportamento geral (crescimento e diminuição).

Abaixo está o gráfico da função polinomial:

f (x) = - x⁴+4x²+1

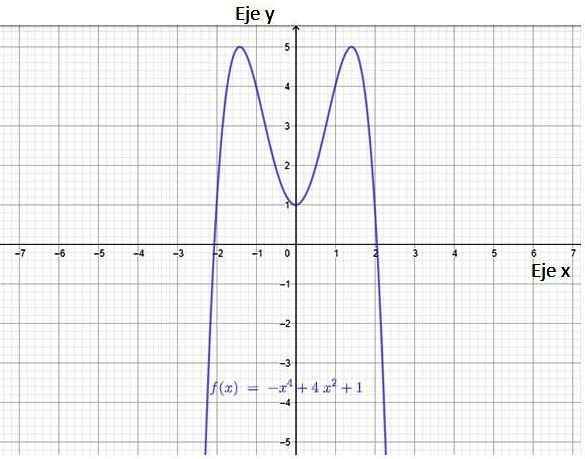Figura 3. Gráfico de uma função polinomial. Fonte: f. Zapata através da Geogebra.

A partir da imagem, segue-se que a função possui dois cruzamentos com o eixo x, os pontos (-2,0) e (2.0). Ele também tem uma interseção com o eixo y, o ponto (0,1).

O domínio de uma função polinomial é o conjunto completo de números reais, também é avisado de que a função é contínua e tem simetria em torno do eixo vertical. De fato, pode -se verificar se esta função é Simetria para. Uma função é mesmo que atenda:

Pode servir a você: teorema verde, demonstração, aplicações e exercícios

f (x) = f (-x)

O leitor pode verificar se substituindo -x na função, não é alterado.

Existem dois pontos interessantes, que estão no auge de y = 5, são os valores máximos da função. O intervalo dessa função, ou seja, o conjunto de valores que a variável leva e, se estende de -∞ a y = 5 precisamente.

Para saber os valores de x cuja imagem é y = 5, esse valor é substituído na função:

5 = - x⁴+4x²+1

E esta equação é obtida:

- x⁴ + 4x² - 4 = 0

Cujas soluções são −√2 e + √2. Bem, a função é:

-Crescente De x -∞ a x = −√2

-Diminuindo De x = −√2 a x = 0

-Crescente De x = 0 a x = + √2

-Diminuindo De x = + √2 em diante.

Exercício resolvido

Crie o gráfico da seguinte função:

f (x) = √ (x-5)

Solução

Primeiro você deve determinar o domínio da função, para saber quais valores de x podem ser escolhidos para construir a tabela. No caso da função proposta, a quantidade dentro da raiz deve sempre ser positiva ou igual a 0, portanto:

x - 5 ≥ 0

x ≥ 5

Portanto, apenas valores maiores ou iguais a 5 podem ser escolhidos para a tabela. Quanto às interseções com os eixos de coordenadas, a única possibilidade é fazer y = 0 e depois x = 5.

É inútil fazer x = 0 para esta função, pois esse valor não pertence ao domínio.

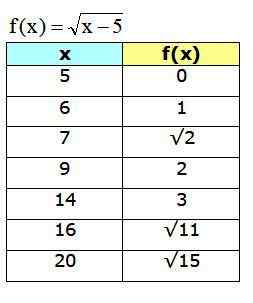
O gráfico obtido é:

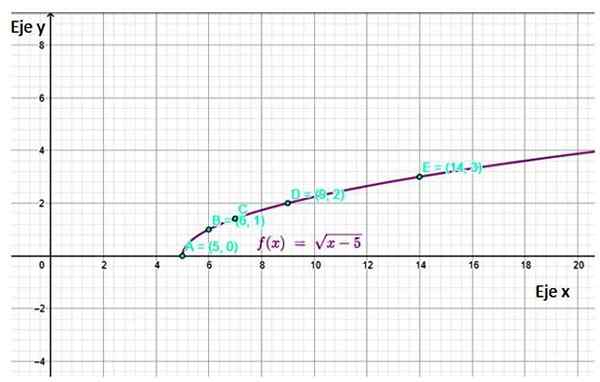Figura 4. Gráfico de função F (x) mostrando alguns dos pontos calculados na tabela. Fonte: f. Zapata através da Geogebra.

Referências

1. Zona de matemática eletrônica. Tipos de funções. Recuperado de: emathzone.com.
2. Hoffman, J.G. Seleção de questões de matemática. Ed. Spphinx.
3. A matemática é divertida. Referência de funções do Commons. Recuperado de: Mathisfun.com.
4. Requena, b. Fórmulas do Universo. Tipos de funções. Recuperado de: universoformulas.com.
5. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.