Função crescente de como identificá -lo, exemplos, exercícios

Você tem um função crescente Quando o valor de y aumenta se o x também aumentar, em oposição às funções decrescentes, nas quais o valor e diminui quando o X aumenta.

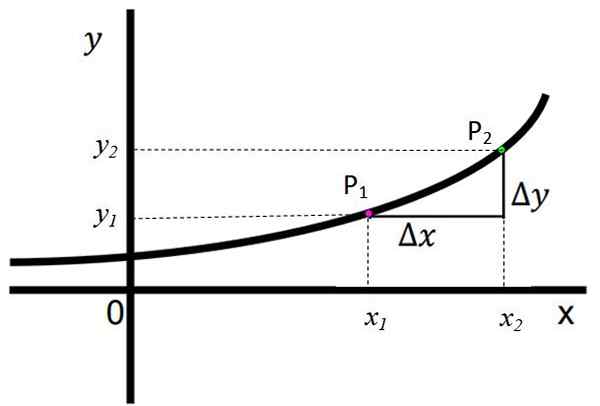
A figura a seguir mostra uma função crescente e observa -se claramente que, ao passar da esquerda para a direita no eixo X, o valor da respectiva coordenada e, equivalente a f (x), está aumentando gradualmente. Dizem que se para tudo x₂ > x₁, Então existe e₂ > e₁.

figura 1. Uma função crescente. Fonte: f. Zapata.

Os pontos p₁ E P₂ Eles são mostrados, eles têm respectivamente, coordenadas (x₁, e₁) e (x₂,e₂). Eles são definidos:

Δy = y₂ -e₁

Δx = x₂ -x₁

Nesta função, Δy e Δx têm um sinal positivo, o que significa que e₂ > e₁ e x₂ > x₁, respectivamente. Este é um sinal claro de que a função cresce efetivamente.

Um bom exemplo de função sempre crescente (crescente monótona) é o logaritmo neperiano de um número real. Quanto maior o número, maior seu logaritmo.

[TOC]

Como identificar uma função crescente?

Em uma função simples e contínua, como mostrado na Figura 1, é fácil determinar se a função está aumentando ou diminuindo, desde que o gráfico esteja disponível.

No entanto, funções mais complexas podem crescer em alguns intervalos e diminuir em outras. É por isso que falamos sobre Intervalos de crescimento e diminuir de uma função.

Na rede, existem gráficos on -line gratuitos, como a Geogebra, que permitem gráficos de todos os tipos de funções. Tendo o gráfico, é fácil determinar se a função está sempre aumentando, como f (x) = log x ou se tem intervalos em que cresce e outros em que diminui e o que são.

Critério da primeira derivada

Considerando um certo intervalo numérico i, se o quociente entre quantidades Δy e Δx for positivo, a função está aumentando. E pelo contrário, se for negativo, a função está diminuindo.

Pode servir a você: probabilidade de frequência: conceito, como é calculado e exemplos

Você tem que:

Δy / Δx> 0 → Função de crescimento

O fato de Δy / Δx> 0 e a função estar aumentando em um determinado intervalo, sugere que o primeiro derivado da função, ou melhor, seu sinal, pode ser usado como critério para determinar se em vigor, a função cresce em um determinado intervalo ou mesmo em um determinado ponto do seu domínio.

De fato, o primeiro derivado é definido como a inclinação da curva todos os pontos:

O que significa que Δx pode ser feito tão pequeno quanto você quiser. Se f '(x)> 0 para um certo valor de x, por exemplo x = a, a inclinação da curva nesse ponto f' (a) for positiva e a função estará aumentando lá.

O teorema a seguir oferece um critério para saber quando uma função está crescendo no intervalo (a, b):

Teorema

Seja f (x) uma função derivável em (a, b). Se f '(x)> 0, para qualquer valor de X pertencente ao referido intervalo, diz -se que f (x) está crescendo (a, b).

O teorema é aplicado para descobrir em que intervalos a função cresce, seguindo estas etapas:

Passo 1

Encontre os pontos em que f '(x) = 0, bem como aqueles em que f' (x) não existe. Estes, chamados Pontos críticos, Esses são pontos em que F '(x) pode mudar de sinal e, portanto, F (x) tem a oportunidade de passar do crescimento para a diminuição ou vice -versa.

Passo 2

Encontre o sinal de f '(x) para o valor arbitrário em cada um dos intervalos determinados pelos pontos encontrados na Etapa 1.

etapa 3

Use o teorema para saber se a função está crescendo ou não em cada intervalo.

Exemplos de funções crescentes

Existem funções que têm alguns intervalos de crescimento e outros de diminuição, mas os mostrados abaixo estão sempre crescendo.

Peso com base na idade

O peso da pessoa desde que nasceu, até o final da adolescência, é quase sempre uma função crescente da idade. Bebês e crianças crescem e se desenvolvem ao longo dos anos e, quando atingem a idade adulta, espera -se que o resto de sua vida mantenha um peso estável, embora os altos e baixos sejam muito frequentes.

Pode atendê -lo: linha vertical

A função logaritmo

As funções do logaritmo variável real neperian f (x) = ln x e logaritmo decimal f (x) = log x estão sempre crescendo.

A função raiz quadrada de um número real

Outra função que está sempre crescendo é a função raiz quadrada de um número real positivo:

y = √x

A função relacionada e a função linear

A função relacionada:

f (x) = mx + b

Está crescendo sempre que a linha é positiva em declive. Da mesma forma, identidade e funções lineares:

f (x) = x e f (x) = ax, com a> 0

Eles estão crescendo em todo o seu domínio.

A função exponencial

Uma função exponencial como f (x) = e^x  E em geral, a função do formulário:

f (x) = a^x, Com um> 1

Eles estão crescendo em todo o seu domínio.

A potencial função de índice impar

As funções potenciais de expoente estranho, como estas:

• f (x) = x³
• g (x) = x⁵

Eles estão sempre crescendo.

Exercícios

Exercício 1

Determine em quais intervalos a função representada no gráfico a seguir está aumentando:

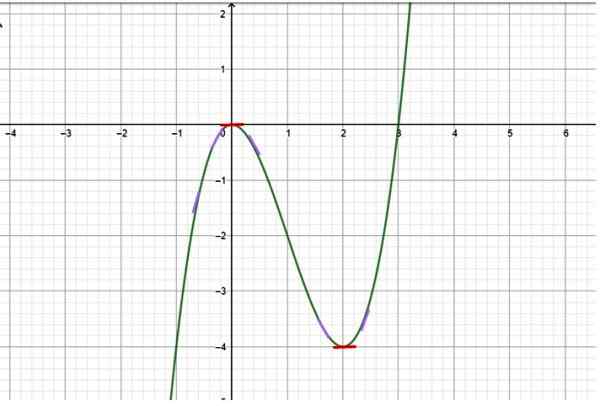Figura 2. Função com crescimento e diminuição de intervalos. Fonte: f. Zapata.

Solução

Como o gráfico está disponível, a partir de sua observação cuidadosa, é determinado que a função tem o seguinte comportamento:

-De x → -∞ a x = 0 a função está aumentando, uma vez que os valores de y se tornam cada vez menos negativos. Pequenos segmentos de inclinação foram desenhados em roxo para indicar a inclinação da linha tangente à curva em vários pontos (a inclinação da tangente à curva é precisamente sua primeira derivada).

Esses segmentos têm uma inclinação positiva, portanto o teorema garante que a função esteja crescendo nesse intervalo.

-Mas em x = 0 a inclinação da curva é cancelada, o que é indicado com um pequeno segmento vermelho horizontal. Este é um ponto crítico da função.

Pode atendê -lo: o que são matemática e para que são? 7 Aplicações importantes

A partir daí, a função começa a diminuir, tornando -se mais negativa os valores de e. Esta situação continua até x = 2, que é outro ponto crítico.

Então, no intervalo de x = 0 a x = 2, a função diminui.

-De x = 2 a função se torna cada vez menos negativa, até que x = 3 cruza o eixo x e continua a se tornar mais positivo a cada vez. Portanto, este é um intervalo de crescimento.

Conclusão: Os intervalos de crescimento são (-∞, 0) e (2, ∞+), enquanto o intervalo de diminuição é (0,2).

Exercício 2

Determine os intervalos de crescimento da seguinte função, através dos critérios da primeira derivada:

f (x) = x² - 2x

Solução

Seguindo as etapas indicadas acima, a primeira derivada é calculada e é igual a 0 para encontrar os pontos críticos:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Este valor determina a existência dos intervalos (-∞, 1) e (1, ∞+). Dois valores arbitrários são escolhidos que pertencem a cada um:

-Para x = 0, que pertence a (-∞, 1), você precisa f '(0) = 2.0 - 2 = -2. Como o resultado é negativo, a função está diminuindo nesse intervalo.

-Para x = 3, pertencente a (1, ∞+), o primeiro derivado vale f '(3) = 2.3 - 2 = 4. Como o resultado é positivo, conclui -se que a função cresce neste intervalo.

O leitor pode representar graficamente a função original f (x) = x² - 2x em um gráfico online para corroborar este resultado.

Referências

1. Ayres, f. 2000. Cálculo. 5ed. Mc Graw Hill.
2. Leithold, l. 1992. Cálculo com geometria analítica. Harla, s.PARA.
3. Purcell, e. J., Varberg, d., & Rigdon, S. E. (2007). Cálculo. México: Pearson Education.
4. Matemobile. Funções, crescendo, diminuindo e constante. Recuperado de: Matemovil.com
5. Requena, b. Funções em crescimento. Recuperado de: universoformulas.com.
6. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.