Fórmula Geral Equações Quadráticas, Exemplos, Exercícios

O Fórmula geral, que também é conhecido como o Fórmula de solvente Em alguns textos, é usado para resolver equações de segundo grau: machado² + BX + C = 0.

Nelas para, b e c Eles são números reais, com a condição de que para é diferente de 0, sendo x O desconhecido. Então, a fórmula geral apresenta a depuração do desconhecido através de uma expressão que envolve os valores de para, b e c da seguinte maneira:

figura 1. A fórmula geral em matemática é usada para resolver equações quadráticas. Fonte: f. Zapata.

E através desta fórmula, você pode encontrar a solução de qualquer segundo grau ou equação quadrática, desde que essa solução exista.

Segundo os historiadores, a fórmula geral já era conhecida pela antiga matemática babilônica. Foi posteriormente transmitido a outros povos, como os egípcios e os gregos, através de trocas culturais.

A fórmula e suas variantes chegaram à Europa, graças aos matemáticos muçulmanos se estabeleceram na Península Ibérica. No entanto, eles não usaram a notação algébrica de que atualmente usamos. Essa notação se deve ao matemático francês e ao especialista em criptográfico do século XVI, Francois Viete.

[TOC]

Equações quadráticas pela fórmula geral

Vamos ver como surge a fórmula geral, a fim de verificar sua validade. Começando de uma equação quadrática geral:

machado² + BX + C = 0

Vamos colocar em prática algumas manipulações algébricas simples, para alcançar a liberação do desconhecido. Existem várias maneiras de carregar isso, por exemplo, completando quadrados, como mostrado então.

Demonstração da fórmula geral

Começamos adicionando (-c) em ambos os lados da igualdade:

machado² + Bx = - c

E agora é multiplicado por 4A, sempre em ambos os lados da igualdade, para não alterar a expressão:

4º² x² + 4ab x = - 4ac

Adicionando b²:

4º²⋅x² + 4AB⋅x + b² = - 4ac + b²

O objetivo disso é completar quadrados no lado esquerdo da igualdade, que contém o desconhecido, dessa maneira sua liberação é facilitada. Desta forma:

Pode atendê -lo: divisores de 8: o que são e uma explicação fácil

-O primeiro termo: 4º² x² É o quadrado perfeito de 2ax

-O último, que é B², É o quadrado perfeito de B.

-E o termo central é o produto duplo de 2ax e b: 2⋅2ax⋅b = 4ABX

Portanto, temos um binomial quadrado:

4º²⋅x² + 4AB⋅x + b² = (2ax + b)²

E podemos escrever:

(2ax + b)² = - 4ac + b²

Estamos a um passo de limpar o desconhecido x:

E já obtemos a fórmula geral que conhecemos:

Existem outras maneiras de manipular algebraicamente a equação quadrática e obter esse mesmo resultado.

Exemplos de uso da fórmula geral

Para aplicar a fórmula geral, os valores de A, B e C são cuidadosamente determinados e substituídos na fórmula. Observe o símbolo mais menos no numerador; Isso indica que devemos considerar duas possibilidades em relação à operação, uma com o sinal + e outro com o sinal -.

A equação quadrática pode ter as seguintes soluções, de acordo com o valor da quantidade subd-radical, conhecida como discriminador:

-Sim B² - 4ac> 0, a equação quadrática tem duas soluções reais e diferentes.

-Quando b² - 4ac = 0, a equação tem uma solução única, dada por:

x = -b/2a

-Finalmente, se B² - 4ac < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Vejamos alguns exemplos em que a fórmula geral é aplicada, percebendo que, se algum dos coeficientes que acompanham o desconhecido não aparecer, entende -se que vale a pena 1. E se o termo independente é o que não é encontrado, vale a pena.

- Exemplo 1

Resolva as seguintes equações quadráticas:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Responda para

Escrevemos os coeficientes de cada termo: a = 6, b = 11, c = -10 e substituímos os valores na fórmula geral:

Pode atendê -lo: Tributação

x = (-11 ± 19) /12

O resultado leva às duas soluções reais a seguir:

x₁ = (-11 + 19)/12 = 8/12 = 2/3

x₂ = (-11 -19)/12 = -5/2

Resposta b

Novamente, os coeficientes são determinados: a = 3, b = -5 e c = -1. Substituindo a fórmula:

Ao contrário do caso anterior, a raiz quadrada de 37 não é um número inteiro, mas também podemos aumentar as duas soluções e deixar a raiz ou encontrar o valor decimal correspondente com a ajuda da calculadora:

x₁ = (-5 + √37)/6 ≈ 0.18

x₂ = (-5 - √37)/6 ≈ - 1.85

- Exemplo 2

Resolva a equação do segundo grau x² - 4x +13 = 0.

Responder

Como sempre, identificamos os valores dos coeficientes e substituímos a fórmula geral: a = 1, b = - 4, c = 13. Isto leva a:

Temos uma raiz negativa; portanto, as soluções desta equação são números complexos. A raiz pode ser expressa em termos de Yo, o Unidade imaginária:

√ (36i²) = 6i

Desde que eu² = -1, portanto, as soluções complexas são:

x₁ = (4 + 6i)/2 = 2 + 3i

x₂ = (4 - 6i)/2 = 2 - 3i

Exercício resolvido

Uma escada de 10 m de comprimento fica contra uma parede vertical, com o pé 6 m daquela parede. A escada desliza e o pé é separado 3 m a mais da base.

Encontre a distância vertical que percorre o topo da escada.

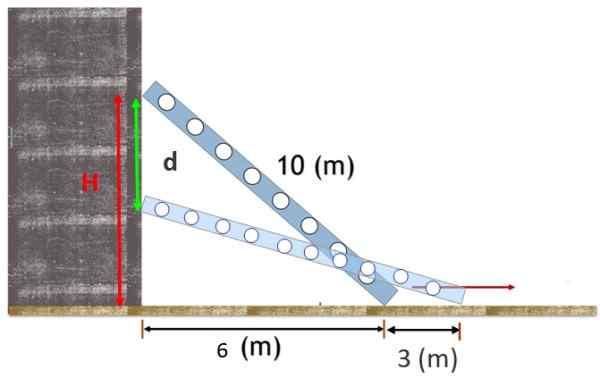Figura 2. Uma escada suportada em uma parede escorrega um pouco e a parada superior se move verticalmente a uma distância D. Fonte: f. Zapata.

Solução

Para encontrar a distância vertical que desliza a parte superior da escada, você precisa encontrar a posição em que ela estava originalmente em relação ao solo. Podemos fazer isso com o teorema de Pitágoras, porque a figura formada é a de um triângulo certo:

H = (10² - 6²) ^½ = 8 m

Uma vez que a escada desliza, uma distância se move d, Medir como o topo tinha 8 m de altura, até atingir sua nova posição, a metros (h-d) acima do solo. O desconhecido para limpar é D.

Pode servir a você: Frequência acumulada: fórmula, cálculo, distribuição, exemplos

Para encontrá -lo, propomos um novo triângulo retângulo, que é formado depois que a escada escorregou um pouco. Este triângulo ainda tem hipotenusa igual a 10 me e o Cateto paralelo é agora 6m + 3m = 9 m, portanto:

(H-d)² = 10² - 9² = 100 - 81 = 19

Substituímos H = 8m, calculado anteriormente:

(8-D)² = 19

A equação pode ser resolvida de várias maneiras, incluindo o uso da fórmula geral, que mostraremos abaixo com estas etapas:

Passo 1

Desenvolva a esquerda notável da esquerda:

64 -16D + D² = 19

Passo 2

Estabelecer a equação de segundo grau para desconhecido d:

d² - 16d + 45 = 0

etapa 3

-Os coeficientes são: a = 1, b = -16 e c = 45, nós os substituímos na fórmula geral:

As soluções da equação são:

d₁ = (16 + √76)/2 ≈ 12.36 m

d₂ = (16 - √76)/2 ≈ 3.64 m

Passo 4

As soluções obtidas são analisadas: a primeira não faz sentido físico, pois não é possível que a escada compile 12.36 m, se originalmente a parada era de 8 m de altura no chão.

Portanto, a resposta correta é a segunda solução: a parte superior da escada desliza d = 3.64 m.

O leitor pode resolver o problema aplicando outro método?

Referências

1. Baldor. 1977. Álgebra Elementar. Edições culturais venezuelanas.
2. Hoffman, J. Seleção de questões de matemática. Volume 2.
3. Jiménez, r. 2008. Álgebra. Prentice Hall.
4. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
5. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.