Coeficiente de atrito estático, exemplo, exercício

O fricção estática É a força que surge entre duas superfícies quando uma superfície não desliza em relação ao outro. É de grande importância, porque nos permite avançar ao caminhar, pois é a força atual entre o piso e a sola dos sapatos. 

É também atrito estático que aparece entre os pneus de pavimento e o carro. Se essa força não estiver presente, é impossível para o carro começar a se mover, como em um carro que tenta começar em uma superfície gelada: as rodas deslizam, mas o carro não avança.

figura 1. Ilustração sobre força de atrito

O atrito estático depende da rugosidade das superfícies em contato e também do tipo de material que é feito. É por isso que os pneus e os sapatos esportivos são de borracha, a fim de aumentar o atrito com a calçada.

No modelo de atrito estático, as características dos materiais e o grau de rugosidade entre as superfícies são resumidas em um número chamado Coeficiente de atrito estático, que é determinado experimentalmente.

[TOC]

Coeficiente de atrito estático

Figura 2. O livro sobre a tabela inclinado permanece em repouso devido à força de atrito estático entre o livro e a tabela. Fonte: f. Zapata.

A figura superior mostra um livro que está em repouso em uma mesa que tem uma inclinação de 15,7º.

Se as superfícies do livro e a mesa fossem muito suaves e polidas, o livro não poderá ser mantido em repouso. Mas como não são, aparece uma força tangente às superfícies em contato chamado força de fricção estática. 

Se o ângulo de inclinação era grande o suficiente, então não há o suficiente fricção estática Para equilibrar o livro e isso começaria a deslizar.

Nesse caso, também há atrito entre o livro e a tabela, mas isso seria um força de Fricção dinâmica, também chamado fricção cinética.

Há uma borda entre atrito estático e atrito dinâmico, que ocorre no momento em que o atrito estático atinge seu valor máximo.

Pode servir a você: Efeito Doppler: Descrição, Fórmulas, Casos, Exemplos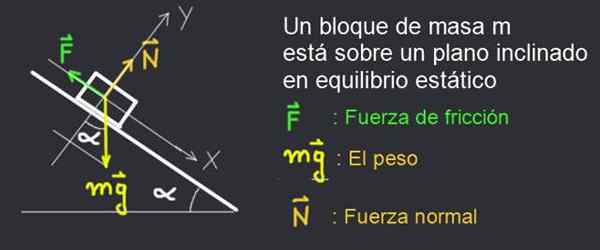Figura 3. Um bloco de descanso em um avião inclinado está em repouso graças à força de atrito estático. Fonte: f. Zapata.

Considere na Figura 2, o diagrama de força de um livro de massa m que permanece em repouso em um plano de inclinação α.

O livro permanece em repouso porque a força de atrito F, tipo estático, equilibra o sistema.

Se o ângulo de inclinação crescer um pouco, as superfícies de contato devem fornecer mais força de atrito, mas a quantidade de lixo estático_Máx, quer dizer:

F ≤ f_Máx.

A força máxima de atrito estático dependerá dos materiais e do grau de rugosidade das superfícies em contato, bem como da firmeza do aperto.

O coeficiente de atrito estático μ_e É um número positivo que depende das características das superfícies em contato. A força normal N que o avião exerce no bloco explica o grau de aperto entre a superfície do bloco e o plano. Assim, eles determinam a força máxima de atrito fornecida pelas superfícies quando não há deslizamento de terra:

F_Máx = μ_e N

Em suma, a força de atrito estático segue o seguinte modelo:

F ≤ μ_e N

Exemplo: Determinação do coeficiente de atrito estático

O coeficiente de fricção estática é um número sem dimensão que é determinado experimentalmente para cada par de superfícies. 

Consideramos o bloco no resto da Figura 2. As seguintes forças agem sobre ele:

- A força de atrito: F

- O peso do bloco de massa m: mg

- A força normal: N

Como o bloco está em repouso e não tem aceleração, de acordo com a Segunda Lei de Newton, a força resultante -uma soma vetorial -é void:

F + N + mg = 0

É considerado um sistema de coordenadas XY fixo com o eixo x ao longo do plano inclinado e o eixo e perpendicular a ele, como mostra a Figura 2.

Pode atendê -lo: ouvir força: forças de superfície e massa

As forças devem ser separadas de acordo com seus componentes cartesianos, dando origem ao seguinte sistema de equações:

-Componente x: -F + mg sen (α) = 0

-Componente e: N - mg cos (α) = 0

Desde a primeira equação, o valor do atrito estático é liberado:

F = mg sen (α)

E do segundo o valor da força normal:

N = mg cos (α)

A força de atrito estático se deve ao seguinte modelo:

F ≤ μ_e N

Substituindo em desigualdade os valores obtidos anteriormente que temos:

mg sen (α) ≤ μ_e mg cos (α)

Levados em consideração que, para os valores de α entre 0º e 90º, as funções senoidal e cosseno são positivas e que o quociente entre a mama e o cosseno é a tangente, deixamos:

Tan (α) ≤ μ_e

A igualdade é cumprida para um valor específico de α chamado ângulo crítico e que indicamos para α*, ou seja::

μ_e = Tan (α*)

O ângulo crítico é determinado experimentalmente, aumentando gradualmente a inclinação para o ângulo certo no qual o bloco começa a deslizar, que é o ângulo crítico α*.

No livro na Figura 1, este ângulo foi determinado experimentalmente, resultando em 24º. Então o coeficiente de atrito estático é:

μ_e = Tan (24º) = 0,45.

É um número positivo entre 0 e o infinito. Sim μ_e = 0 superfícies são perfeitamente suaves. Sim μ_e → ∞ As superfícies estão perfeitamente ligadas ou soldadas.

Geralmente o valor do coeficiente de atrito está entre 0 e 10.

Exercício

Nas raças ou dragsters de pique, acelerações de até 4G são alcançadas durante o início, que são alcançadas com precisão quando os pneus não deslizam em relação ao pavimento.

Isso ocorre porque o coeficiente de atrito estático é sempre maior que o coeficiente de atrito dinâmico.

Supondo que o peso total do veículo mais o motorista seja de 600 kg e que as rodas traseiras suportem 80% do peso, determine a força de atrito estático durante a partida 4G e o coeficiente de atrito estático entre os pneus e o pavimento.

Pode servir a você: Orion Nebula: Origem, Localização, Características e DadosFigura 4. Um "dragster" no momento do início. Fonte: Pixabay.

Solução

De acordo com a segunda lei de Newton, a força resultante é igual à massa total de veículo devido à aceleração que adquire.

Como o veículo está em equilíbrio vertical, o normal e o peso são anulados restantes como uma força resultante de atrito para que o pavimento exerça na área de contato das rodas de tração, permanecendo que:

F = m (4g) = 600 kg (4 x 9,8 m/s²) = 23520 n = 2400 kg-f

Ou seja, a força de tração é de 2,4 toneladas.

A força de atrito que a roda exerce no chão remonta, mas sua reação que é a mesma e atos opostos no pneu e vai adiante. Essa é a força que dirige o veículo.

Obviamente, toda essa força é produzida pelo motor que, através da roda, tenta empurrar o chão para trás, mas a roda e o piso são acoplados pela força de atrito. 

Para determinar o coeficiente de atrito estático, usamos o fato de que o F obtido é o máximo de atrito possível, pois estamos no limite máximo de aceleração: portanto:

F = μ_e N = μE (0,8 mg)

O fato de que as rodas traseiras de tração suportam 0,8 vezes o peso foi levado em consideração. Limpando o coeficiente de atrito é obtido:

μ_e = F / (0,8 mg) = 23520 n / (0,8 x 600 kg x 9,8 m / s^2) = 5.

Conclusão: μ_e = 5.

Referências

1. Alonso m., Finn e. 1970. Volume da física I: mecânica. Fundo Educacional Inter -Americano.PARA.
2. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
3. Hewitt, p. 2012. Ciência física conceitual. QUINTA EDIÇÃO.
4. Rex, a. 2011. Fundamentos da Física. Pearson. 190-200.
5. Jovem, Hugh. 2015. Física da Universidade com Física Moderna. 14ª ed. Pearson.