Frações equivalentes a 2/3

As frações equivalentes a ⅔ (Dois terços são lidos) são aqueles cujo valor, expresso de maneira decimal, é o mesmo que é obtido dividindo 2 por 3: 0.6666… os pontos suspeitos indicam que 6 parece infinita tempos nesta divisão.

Uma fração equivalente a 2/3 é a fração 4/6, pois, depois de resolver a divisão entre 4 e 6 explicitamente, o Decimal 0,6666 .. . Então pode -se dizer que 4/6 = 2/3 = 0,6666 .. .

As frações 2/3 e 4/6 são equivalentes porque dividindo o número do numerador pelo denominador Figura o mesmo jornal número 0.66666 .. . (Fonte: F. Zapata)

Uma fração, como o nome indica, é uma parte ou parte da unidade. A fração ⅔ é obtida dividindo a unidade em três partes iguais e pegando duas dessas partes.

Cada fração consiste em uma parte superior, chamada numerador, separado do fundo ou denominador, Através da linha de fração. O denominador indica quantas partes a unidade está dividida e o numerador indica quantas dessas partes devem ser levadas em consideração.

Agora considere a fração 4/6 (leia quatro sexto). Está provado que essa fração é equivalente a ⅔, pois, para dividir a unidade em seis partes, essas etapas devem ser seguidas:

1. Divida a unidade em três partes iguais.
2. E depois divida cada uma dessas partes pela metade, obtendo no total seis partes iguais.

Se 4 partes de 1/6 da unidade estiverem agrupadas, a quantidade obtida é uma fração de valor idêntico ao qual 2 partes de 1/3 da unidade são obtidas. No gráfico seguinte, o procedimento descrito é realizado: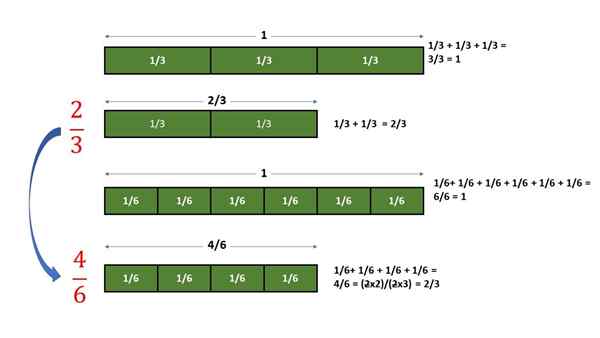

Verificação gráfica de que a fração 2/3 é equivalente à fração 4/6. Fonte: f. Zapata.

Pode atendê -lo: analogias numéricas: tipos, aplicações e exercícios

Métodos para encontrar frações equivalentes

Observe que a fração equivalente 4/6 pode ser obtida de 2/3 multiplicando pelo numerador e pelo denominador deste último.

Quando simultaneamente multiplica o numerador e o denominador de uma fração pelo mesmo número, uma fração equivalente é obtida.

Outra maneira de encontrar uma fração equivalente a outra seria dividir o numerador e o denominador pela mesma quantidade, desde que o numerador e o denominador sejam exatamente divisíveis por esse mesmo número. Mas não é possível alcançar, por divisão pelo mesmo número inteiro, uma fração equivalente baseada em 2/3, uma vez que os números 2 e 3 são primos entre si.

Quando o numerador e o denominador de uma fração são números primos, diz -se que a fração é irredutível. E a fração 2/3 é um bom exemplo desse tipo de frações, de fato, 2/3 representa o conjunto de todas as frações equivalentes a 0.666 ..

Por outro lado, a fração 4/6 é redutível e equivalente à fração ⅔, pois o numerador 4 e o denominador 6 são números uniformes, ambos divisíveis por 2.

Então, as duas maneiras de obter frações equivalentes a um dado são:

• Amplificar simultaneamente numerador e denominador 
• Reduza o numerador e denominador

Amplificação de frações

Para obter uma fração equivalente a um dado, numerador e denominador são multiplicados pela mesma figura. aqui estão alguns exemplos:

It is concluded that ⅔ (two thirds), 4/6 (four sixth), 6/9 (six ninth) and 8/12 (eight twelfths) are all equivalent fractions with each other, but of them, only ⅔ is the irreducible fração.

Em resumo, se você começar com a fração irredutível ⅔, a maneira de obter qualquer outra fração equivalente é aplicar esta fórmula:

Pode atendê -lo: exercícios de fatoração resolvidos

Com um número inteiro.

Método de amplificação para obter frações equivalentes. Fonte: f. Zapata

Redução de frações

É um método que permite que uma fração equivalente seja obtida, desde que a fração inicial tenha um numerador e denominador com um ou mais divisores comuns.

Não é o caso de 2/3, que, como dito antes, é irredutível. Mas por exemplo, fração 60/90 (Sessenta anos) Pode ser reduzido para:

• 6/9, já que o numerador e o denominador são divisíveis entre dez.
• 30/45, porque o numerador e o denominador são divisíveis entre dois.
• 20/30, já que o numerador e o denominador são divisíveis entre três.
• 12/18, porque o numerador e o denominador são divisíveis entre cinco.

Se você deseja obter a fração irredutível equivalente ao original, é necessário dividir o numerador e o denominador por seu divisor comum máximo (MCD).

Decomposição em fatores que o numerador possui:

60 = 2² ⋅ 3 ⋅ 5

E realizar o mesmo procedimento no denominador:

90 = 2 ⋅ 3² ⋅ 5

O MCM são os fatores primos comuns com seu expoente mais baixo, ou seja:

Mcm (60; 90) = 2⋅3⋅5 = 30

Então, 60 entre 30 Da 2, que é colocado no numerador e em 90 entre 30 Da 3, 3 é colocado no denominador. Portanto, a fração irredutível 60/90 pode ser expressa como:

Maneiras de determinar se uma determinada fração é equivalente a 2/3

A maneira direta de saber se duas ou mais frações são equivalentes, é expressar as frações diretamente de maneira decimal, e se todos os dígitos coincidem, é certo que as frações são equivalentes. Mas existem outros métodos aplicáveis ​​a 2/3:

Método 1

Seja fração x/y Você quer saber se essa fração é equivalente a 2/3:

Um sinal de interrogatório é colocado, porque ainda não se sabe se os valores de "x" e "y" satisfazem a igualdade. Saber isso se multiplica em cruz:

Pode atendê -lo: relações de proporcionalidade: conceito, exemplos e exercícios

3x =? 2 e

Somente quando a igualdade é cumprida, há certeza de que x/y é uma fração equivalente a 2/3.

Método 2

Este método requer a determinação do divisor comum máximo (MCD) do numerador e do denominador. Então ambos são divididos pelo MCD e, se a fração obtida após a execução da operação descrita é 2/3, pode -se dizer que é uma fração equivalente a ele.

Exemplos

Exemplo 1

Determine se a fração 40/60 é equivalente a ⅔.

Solução

Pelo método 1:

O método indica que deve ser multiplicado em cruz:

40 x 3 =? 60 x 2

120 =? 120

Como a igualdade é cumprida, conclui -se que 40/60 é equivalente a 2/3.

Exemplo 2

Determine se a fração 120/180 é equivalente a ⅔.

Solução

Neste exemplo, o método 2 se aplica. A primeira coisa é determinar a decomposição em fatores primos de 120:

120 = 2³ ⋅ 3 ⋅ 5

E a decomposição em fatores denominadores é:

180 = 2² ⋅ 3² ⋅ 5

Para determinar o MCD, os fatores comuns são multiplicados com seu expoente mais baixo:

MCD (120; 180) = 2² ⋅ 3 ⋅ 5 = 60

Então:

120 ÷ 60 = 2

180 ÷ 60 = 3

Portanto, conclui -se que 120/180 é equivalente a 2/3, ou seja:

Exercícios resolvidos

Exercício 1

São frações 10/15 e 12/18 equivalentes?

Solução

A maneira mais rápida de verificar é se multiplicar em uma cruz, pois não são valores muito grandes:

10 x 18 =? 15 x 12

180 =? 180

Uma igualdade foi obtida, então pode -se dizer que 10/15 = 12/18.

Exercício 2

São frações 8/12 e 12/20 equivalentes a ⅔?

Solução

O método de simplificação será aplicado, que consiste em dividir o numerador e o denominador simultaneamente por fatores primos comuns até atingir uma expressão irredutível:

12/12 = 4/6 = ⅔, isto é, a primeira fração é equivalente a ⅔.

Para a segunda fração que você tem:

12/20 = 6/10 = ⅗, mas ⅗ é irredutível e diferente de ⅔, portanto, a segunda fração não é igual a ⅔.