Factoria

Qual é a fatoração?

A fatorização é um método pelo qual um polinômio é expresso na forma de multiplicação de fatores, que podem ser números, letras ou ambos. Para levar em consideração, os fatores que são comuns aos termos são agrupados e, dessa maneira, o polinomial é decomposto em vários polinômios.

Assim, quando os fatores se multiplicam, o resultado é o polinômio original. A fatoração é um método muito útil quando há expressões algébricas, porque pode se tornar a multiplicação de vários termos simples; Por exemplo: 2º² + 2AB = 2a _* (A + b).

Há casos em que um polinômio não pode ser fatorizado porque não há fator comum entre seus termos; Assim, essas expressões algébricas são divisíveis apenas entre si e por 1. Por exemplo: x + y + z.

Em uma expressão algébrica, o fator comum é o divisor comum máximo dos termos que o compõem.

Métodos de fatoração

Existem vários métodos de fatorização, que são aplicados dependendo do caso. Alguns deles são os seguintes:

Fatoração comum

Neste método, os fatores comuns são identificados; isto é, aqueles que são repetidos nos termos da expressão. Em seguida, a propriedade distributiva é aplicada, o divisor comum máximo é removido e a fatoração é concluída.

Em outras palavras, o fator comum da expressão é identificado e cada termo é dividido entre isso; Os termos resultantes serão multiplicados pelo divisor comum máximo para expressar a fatorização.

Exemplo 1

Fatore (b²x) + (b²e).

Solução

Primeiro é o fator comum de cada termo, que neste caso é B², E então os termos são divididos entre o fator comum da seguinte forma:

(b²x) / b² = x

(b²y) / b² = y.

A fatoração é expressa, multiplicando o fator comum pelos termos resultantes:

(b²x) + (b²y) = b² (x + y).

Exemplo 2

Facione (2º²b³) + (3AB²).

Solução

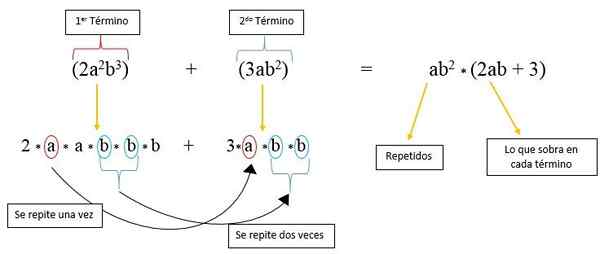
Nesse caso, temos dois fatores que são repetidos em cada termo que são "A" e "B", e que são elevados a um poder. Para considerá -los primeiro, os dois termos são divididos em sua forma longa:

2_*para_*para_*b_*b_*B + 3a_*b_*b

Pode -se observar que o fator "A" é repetido apenas uma vez no segundo termo, e o fator "B" é repetido duas vezes nisso; Portanto, no primeiro termo, há apenas 2, um fator "A" e um "B"; Enquanto no segundo termo, apenas 3 permanece.

Portanto, está escrito quantas vezes que "A" e "B" são repetidas e multiplicadas pelos fatores que restam de cada termo, conforme observado na imagem:

Fator de agrupamento

Como não, em todos os casos.

Pode servir a você: seções cônicas: tipos, aplicações, exemplos

Uma dessas etapas é agrupar os termos do polinomial em vários grupos e depois usar o método de fator comum.

Exemplo 1

Fature AC + BC + AD + BD.

Solução

Existem 4 fatores em que dois são comuns: no primeiro termo, é "c" e no segundo é "d". Dessa forma, os dois termos são agrupados e separados:

(AC + BC) + (AD + BD).

Agora é possível aplicar o método de fator comum, dividindo cada termo por seu fator comum e, em seguida, multiplicando esse fator comum pelos termos resultantes, como este:

(AC + BC) / C = A + B

(ad + bd) / d = a + b

C (a + b) + d (a + b).

Agora é obtido um binomial que é comum para ambos os termos. Para levar em consideração, é multiplicado pelos demais fatores; Dessa forma, você tem que:

AC + BC + AD + BD =  (C + D) _* (A + b).

Fatoração de inspeção

Este método é usado para faturar polinômios quadráticos, também chamados trinômios; isto é, aqueles que são estruturados como machado² ± bx + c, onde o valor de "A" é diferente de 1. Este método também é usado quando o trinomial tem a forma x² ± bx + c e o valor de "a" = 1.

Exemplo 1

Fator x² + 5x + 6.

Solução

Você tem um trinômio quadrático da forma x² ± bx + c. Para levar em consideração primeiro, dois números devem ser encontrados que, ao multiplicar, resulta no valor "C" (ou seja, 6) e que sua soma é igual ao coeficiente "B". Esses números são 2 e 3:

2 _* 3 = 6

2 + 3 = 5.

Dessa maneira, a expressão é simplificada da seguinte maneira:

(x² + 2x) + (3x + 6)

Cada termo é fator:

• Para (x² + 2x) O termo comum é removido: x (x + 2)
• Para (3x + 6) = 3 (x + 2)

Assim, a expressão permanece:

x (x +2) +3 (x +2).

Como você tem um binomial comum, para reduzir a expressão, ele multiplica isso por termos restantes e precisa:

x² + 5x + 6 = (x + 2) _* (x + 3).

Exemplo 2

Fature 4a² + 12a +9 = 0.

Solução

Você tem um trinômio quadrático da forma de machado² ± bx + c e para faturar ele multiplica toda a expressão pelo coeficiente de x²; Nesse caso, 4.

4º² + 12a +9 = 0

4º² (4) + 12a (4) + 9 (4) = 0 (4)

16 a² + 12a (4) + 36 = 0

4² para² + 12a (4) + 36 = 0

Agora, deve -se descobrir dois números que, ao se multiplicar, resultam no valor de "C" (que é 36) e que, ao ingressar no coeficiente do termo "A", que é 6.

6 _* 6 = 36

6 + 6 = 12.

Dessa forma, a expressão é reescrita, levando em consideração que 4² para² = 4a _* 4º. Portanto, a propriedade distributiva é aplicada a cada termo:

Pode servir você: caixa de mackinder

(4a + 6) _* (4a + 6).

Finalmente, a expressão é dividida pelo coeficiente de um²; isto é, 4:

(4a + 6) _* (4a + 6) / 4 = ((4a + 6) / 2) _* ((4a + 6)/ 2).

A expressão é a seguinte:

4º² + 12a +9 = (2a +3) _* (2a + 3).

Fatoração com produtos notáveis

Há casos em que, para levar em consideração completamente os polinômios com os métodos anteriores, torna -se um processo muito longo.

É por isso que uma expressão pode ser desenvolvida com as fórmulas de produtos notáveis ​​e, portanto, o processo se torna mais simples. Entre os produtos notáveis ​​mais usados ​​estão:

• Diferença de dois quadrados: (a² - b²) = (a - b) _* (A + b)
• Quadrado perfeito de uma soma: um² + 2AB +b² = (a + b)²
• Quadrado perfeito de diferença: um² - 2AB + b² = (a - b)²
• Diferença de dois cubos: um³ - b³ = (a-b)_*(para² + ab + b²)
• Soma de dois cubos: um³ - b³ = (a + b) _* (para² - ab + b²)

Exemplo 1

Fatore (5² - x²)

Solução

Nesse caso, há uma diferença de dois quadrados; Portanto, a fórmula do produto notável é aplicada:

(para² - b²) = (a - b) _* (A + b)

(5² - x²) = (5 - x) _* (5 + x)

Exemplo 2

Fature 16x² + 40x + 25²

Solução

Nesse caso, há um quadrado perfeito de uma soma, porque dois termos quadrados podem ser identificados, e o termo sobra é o resultado de multiplicar dois pela raiz quadrada do primeiro termo, pela raiz quadrada do segundo termo.

para² + 2AB +b² = (a + b)²

Para levar em consideração, apenas as raízes quadradas do primeiro e terceiro termo são calculadas:

√ (16x²) = 4x

√ (25²) = 5.

Em seguida, os dois termos resultantes são expressos separados pelo sinal da operação, e todo o polinômio quadrado é elevado:

16x² + 40x + 25² = (4x + 5)².

Exemplo 3

Fatore 27a³ - b³

Solução

A expressão representa uma subtração na qual dois fatores são elevados ao cubo. Para levar em consideração, é aplicada a fórmula do produto notável da diferença nos cubos, que é:

para³ - b³ = (a-b)_*(para² + ab + b²)

Assim, para levar em consideração, a raiz cúbica é removida de cada termo do binomial e multiplicada pelo quadrado do primeiro termo, mais o produto do primeiro pelo segundo termo, mais o segundo termo ao quadrado.

27a³ - b³

³√ (27a³) = 3a

³√ (-b³) = -b

27a³ - b³ = (3a - b) _* [(3a)² + 3AB + b²)]

27a³ - b³ = (3a - b) _* (9a² + 3AB + b²)

Fatoração com a regra de Ruffini

Este método é usado quando você tem um polinômio de grau maior que dois, a fim de simplificar a expressão para vários polinômios menores.

Exemplo 1

Fatorice q (x) = x⁴ - 9x² + 4x + 12

Solução

Primeiro, os números que são divisores de 12 são procurados, que é o termo independente; Estes são ± 1, ± 2, ± 3, ± 4, ± 6 e ± 12.

Pode atendê -lo: múltiplos de 2: o que são e explicação

Em seguida, o X é substituído por esses valores, do menos para o maior e, portanto, é determinado com qual dos valores a divisão será exata; isto é, o resto deve ser 0:

x = -1

Q (-1) = (-1)⁴ - 9 (-1)² + 4 (-1) + 12 = 0.

x = 1

Q (1) = 1⁴ - 9 (1)² + 4 (1) + 12 = 8 ≠ 0.

x = 2

Q (2) = 2⁴ - 9 (2)² + 4 (2) + 12 = 0.

E assim por diante para cada divisor. Nesse caso, os fatores encontrados são para x = -1 e x = 2.

O método Ruffini agora é aplicado, segundo o qual os coeficientes de expressão serão divididos pelos fatores encontrados para que a divisão seja exata. Os termos polinomiais são ordenados de maior a menor expoente; No caso em que um termo está ausente com o grau que se segue na sequência, um 0 é colocado no lugar.

Os coeficientes estão localizados em um esquema, como visto na imagem a seguir.

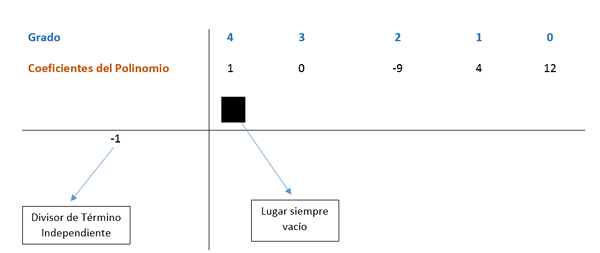
O primeiro coeficiente é reduzido e multiplicado pelo divisor. Nesse caso, o primeiro divisor é -1 e o resultado é colocado na coluna seguinte. Então o valor do coeficiente com esse resultado obtido é adicionado verticalmente e o resultado é colocado abaixo. Dessa forma, o processo é repetido até a última coluna.

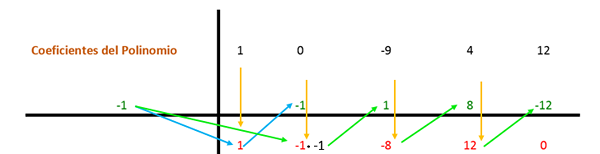
Então o mesmo procedimento é repetido novamente, mas com o segundo divisor (que é 2) porque a expressão ainda pode ser simplificada.

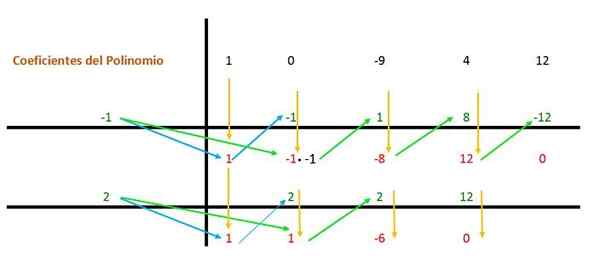
Assim, para cada raiz alcançada, o polinômio terá um termo (x - a), onde "a" é o valor da raiz:

(x - (-1)) _* (x - 2) = (x + 1) _* (x - 2)

Por outro lado, esses termos devem ser multiplicados pelo restante que restava da regra de Ruffini 1: 1 e -6, que são fatores que representam um grau. Dessa maneira, a expressão se forma é: (x² + X - 6).

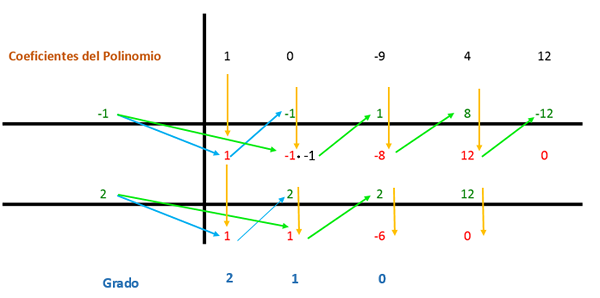
Obter o resultado da fatoração polinomial pelo método de Ruffini é:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2) _* (x² + X - 6)

Finalmente, o polinômio de grau 2 que aparece na expressão anterior pode ser reescrito como (x+3) (x-2). Portanto, a fatoração final é:

x⁴ - 9x² + 4x + 12 = (x + 1) _* (x - 2)_*(x+3)_*(X-2).

Referências

1. Arthur Goodman, L. H. (mil novecentos e noventa e seis). Álgebra e trigonometria com geometria analítica. Pearson Education.
2. J, v. (2014). Como ensinar as crianças sobre considerando um polinômio.
3. Manuel Morillo, um. S. (s.F.). Matemática Básica com Aplicações.
4. Roelse, p. eu. (1997). Métodos lineares para fatoração polinomial sobre campos finitos: teoria e implementações. Universidade Essen.
5. Sharpe, d. (1987). Anéis e fatorização.