Fator de compressibilidade Como calcular, exemplos e exercícios

Ele Fator de compressibilidade Z, o Fator de compressão para gases, é um valor adimensional (sem unidades) que é introduzido como uma correção na equação de status de gases ideal. Dessa maneira, o modelo matemático se assemelha ao comportamento observado do gás mais.

No gás ideal, a equação de estado relacionada às variáveis ​​P (pressão), V (volume) e t (temperatura) é: P.V _ideal = n.R.T com n = número de moles e r = constante dos gases ideais. Adicionando a correção do fator de compressão Z, esta equação é transformada em:

P.V = z.n.R.T

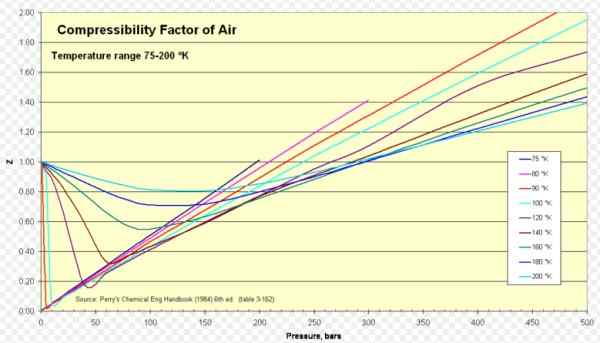
figura 1. Fator de compressibilidade do ar. Fonte: Wikimedia Commons. https: // upload.Wikimedia.org/wikipedia/commons/8/84/compressibility_factor_of_air_75-200_k.Png.

[TOC]

Como calcular o fator de compressibilidade?

Levando em consideração que o volume molar é V_legal = V/n, Você tem o volume molar real:

P . V_real = Z. R. T → Z = PV _real/Rt

Como o fator de compressibilidade Z depende das condições do gás, ele é expresso em função da pressão e da temperatura:

Z = z (p, t)

Comparando as duas primeiras equações, observa -se que, se o número de moles n for igual a 1, o volume molar de um gás real está relacionado ao do gás ideal através de:

V_real / V_ideal = Z → v _real = Z v_ideal

Quando a pressão excede as três atmosferas, a maioria dos gases para de se comportar como gases ideais e o volume real difere significativamente do ideal.

Isso percebeu em seus experimentos o físico holandês Johannes van der Waals (1837-1923), o que o levou a criar um modelo que melhor se ajustou aos resultados práticos do que a equação dos gases ideais: a equação do estado de van der Waals.

Pode atendê -lo: oxalato de sódio (Na2C2O4): estrutura, propriedades, usos, riscos

Exemplos

De acordo com a equação P.V_real= Z.n.Rt, Para um gás ideal, z = 1. No entanto, em gases reais, aumentando a pressão também faz o valor de z. Isso faz sentido porque, em maiores moléculas de gás de pressão, têm mais oportunidades de colidir, portanto as forças de repulsa aumentam e, portanto, o volume.

Por outro lado, para reduzir as pressões, as moléculas se movem com maior liberdade e as forças de repulsa diminuem. Portanto, é esperado um volume mais baixo. Quanto à temperatura, quando aumenta, Z diminui.

Como van der Waals observou, nas proximidades do ponto crítico assim chamado, o comportamento do gás é muito desviado de um gás ideal.

O ponto crítico (t_c, P_c) de qualquer substância são os valores de pressão e temperatura que determinam seu comportamento antes de uma mudança de fase:

-T_c É a temperatura acima do qual o gás em questão não é liquefeito.

-P_c  É a pressão mínima necessária para liquefazer o gás à temperatura t_c

Cada gás tem seu próprio ponto crítico, no entanto, definindo a temperatura e a pressão reduzida t_r E P_r da seguinte forma:

P_r = P / p_c

V_r = V /v_c

T_r = T /T_c

Observa -se que um gás confinado com idêntico V_r e T_r exercer a mesma pressão P_r. Por esse motivo, se z é gráfico, dependendo de P_r para o mesmo T_r, Cada ponto nessa curva é o mesmo para qualquer gás. Isso é chamado Princípio dos estados correspondentes.

O fator de compressibilidade em gases ideais, ar, hidrogênio e água

Abaixo está uma curva de compressibilidade para vários gases em diferentes temperaturas reduzidas. Em seguida, alguns exemplos de z para alguns gases e um procedimento para encontrar z usando a curva.

Pode atendê -lo: hidrogênio: história, estrutura, propriedades e usos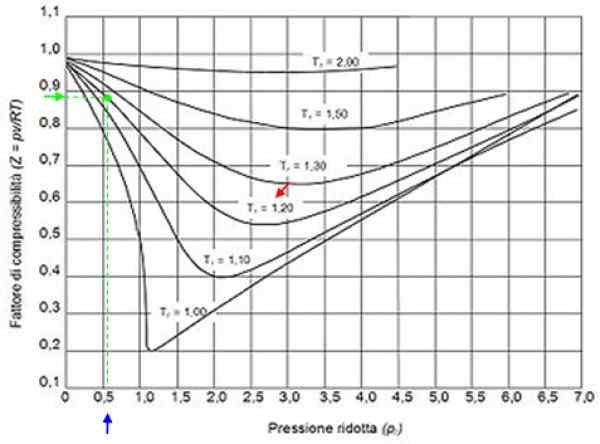Figura 2. Gráficos de fatores gráficos para gases de acordo com a pressão de redução. Fonte: Wikimedia Commons.

Gases ideais

Os gases ideais têm z = 1, conforme explicado no início.

Ar

Para o ar Z é de aproximadamente 1 em uma extensa gama de temperaturas e pressões (veja a Figura 1), onde o modelo de gás ideal fornece resultados muito bons.

Hidrogênio

Z> 1 para todas as pressões.

Água

Para encontrar z da água, os valores do ponto crítico são necessários. O ponto crítico da água é: P_c = 22.09 MPA e T_c= 374.14 ° C (647.3 k). Novamente, é necessário levar em consideração que o fator de compressibilidade z depende da temperatura e pressão.

Por exemplo, suponha que você queira encontrar z da água a 500 ºC e 12 MPa. Então o primeiro é calcular a temperatura reduzida, para a qual os graus Celsius devem ser passados ​​para Kelvin: 50 ºC = 773 K:

T_r = 773/647.3 = 1.2

P_r = 12 /22.09 = 0.54

Com esses valores que localizamos no gráfico da figura, a curva correspondente a T_r = 1.2, indicado com uma seta vermelha. Então olhamos no eixo horizontal o valor de P_r mais perto de 0.54, marcado em azul. Agora desenhamos uma vertical até interceptar a curva t_r = 1.2 e finalmente é projetado a partir desse ponto para o eixo vertical, onde lemos o valor aproximado de z = 0.89.

Exercícios resolvidos

Exercício 1

Há uma amostra de gás a uma temperatura de 350 K e uma pressão de 12 atmosferas, com um volume molar 12 % maior que o previsto pela lei ideal para gases. Calcular:

a) Z fator de compressão.

b) Volume molar de gás.

Pode atendê -lo: reação irreversível: características e exemplos

c) De acordo com os resultados acima, indique quais são as forças dominantes nesta amostra de gás.

Dados: r = 0,082 l.atm/mol.K

Solução para

Sabendo que v _real  é 12 % maior que V_ideal :

V_real  = 1.12V_ideal

Z = v _real / V_ideal = 1.12

Solução b

P . V_real = Z. R. T → V_real = (1.12 x 0.082 x 350/12) l /mol = 2.14 l/mol.

Solução c

As forças de repulsão são aquelas que predominam, uma vez que o volume da amostra aumentou.

Exercício 2

Existem 10 moles de etano confinados em um volume de 4.86 l A 27 ºC. Encontre a pressão exercida pelo etano de:

a) O modelo de gás ideal

b) a equação de van der Waals

c) Encontre o fator de compressão dos resultados anteriores.

Dados para etano

Van der Waals Coeficientes:

A = 5.489 dm⁶. Atm . mol^-2  e b = 0.06380 dm³. mol^-1.

Pressão crítica: 49 atm. Temperatura crítica: 305 K

Solução para

A temperatura é passada para Kelvin: 27 º C = 27 +273 K = 300 K, lembre -se também de que 1 litro = 1 L = 1 dm³.

Em seguida, os dados fornecidos na equação de gás ideal são substituídos:

P.V = n.R.T → p = (10 x 0,082 x 300/4.86 l) atm = 50.6 atm

Solução b

A equação do estado de van der Waals é:

Onde A e B são os coeficientes dados pela declaração. Ao limpar P:

Solução c

Calculamos a pressão e a temperatura reduzidas:

P_r = 35.2/49 = 0.72

T_r = 300 /305 = 0.98 ≈ 1

Com esses valores, é procurado o valor de z no gráfico da Figura 2, descobrindo que z é aproximadamente 0.7.

 Referências

1. Atkins, p. 1999. Química Física. Edições Omega.
2. Cengel, e. 2012. Termodinâmica. 7^MA Edição. McGraw Hill.
3. Engel, t. 2007. Introdução à físico -química: termodinâmica. Pearson.
4. Levine, i. 2014. Princípios da física-química. 6º. Edição. McGraw Hill.
5. Wikipedia. Fator de compressibilidade. Recuperado de: em.Wikipedia.org.