Avaliação de funções

Para avaliar uma função da qual o diagrama é conhecido, por um determinado valor ou elemento do conjunto inicial, é suficiente para observar o elemento correspondente no conjunto de chegada. Fonte: f. Zapata.

Qual é a avaliação das funções?

O Avaliação de funções Consiste em determinar a imagem de um certo valor de domínio. Em outras palavras, para um determinado valor do conjunto inicial, você deve encontrar o seu conjunto correspondente no conjunto de chegada.

Uma função pode ser representada de várias maneiras. Se, por exemplo, o diagrama de Venn estiver disponível, a avaliação é muito simples, é suficiente para selecionar o elemento do conjunto inicial ou domínio e ver o elemento que corresponde ao conjunto de chegada.

En el diagrama de la función “… es capital de… ”, representado arriba, al evaluar dicha función en el elemento “Canadá”, resulta el elemento “Ottawa”, en caso de hacerlo con “México”, resulta “Ciudad de México” e assim por diante.

Se a função for dada na forma de pares arrumados, a avaliação também é simples: o segundo membro do torque ordenado é a imagem do primeiro membro. Por exemplo, com a função f (x) descrita por:

f (x) = (0.0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Ao avaliar a função do valor 3, o resultado é 6; Ao avaliar para 5, é 10 e assim por diante.

Da mesma forma, uma função pode ser avaliada quando o gráfico está disponível, desde que o valor que você deseja avaliar aparece nele.

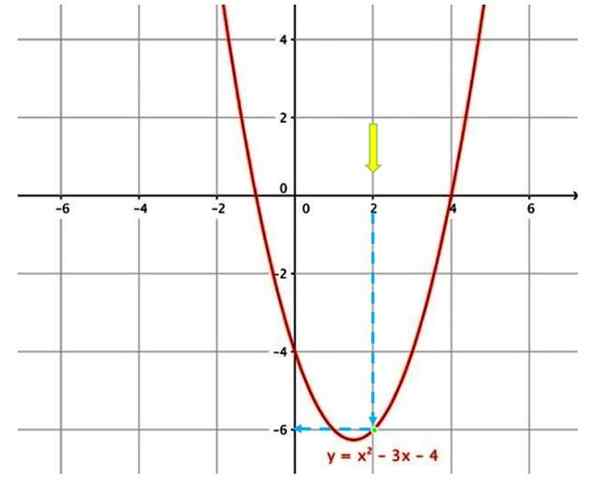Gráfico para avaliar uma função

Por exemplo, para avaliar a função mostrada acima, em x = 2, a primeira coisa é localizar no gráfico a x = 2 (seta amarela).

Então, você tem que se mover após a seta vertical azul, até tocar na curva (ponto verde). Siga a seta azul novamente, o que indica o valor correspondente no eixo vertical, portanto, ao avaliar a função em x = 2, y = −6 é obtida.

Pode atendê -lo: funções trigonométricas: básico, no avião cartesiano, exemplos, exercícios

Avalie uma determinada função na notação matemática

Na parte inferior do gráfico acima, a função gráfica aparece, mas dada em notação matemática, ou seja, através de uma fórmula:

f (x) = x² - 3x - 4

Quando você deseja avaliar a função em qualquer valor x = a, você precisa encontrar f (a), que é simplesmente lido "f de um".

Para encontrar o resultado, x = a é substituído na fórmula da função, e as operações e cálculos solicitados são realizados por aí.

Suponha que você queira avaliar a função do exemplo em x = −1. Isso significa que F (-1) deve ser encontrado.

O primeiro passo é substituir x = -1 na função:

f (−1) = (−1)² - 3 ∙ (−1) - 4

E então, realize as operações indicadas, que neste exemplo são:

• Encontre o quadrado de -1: (−1)² = 1
• Subtrair o valor anterior do produto 3 ∙ (−1): 3 ∙ (−1) = −3
• Do resultado anterior, subtraia 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

O leitor pode corroborar esse resultado, a partir do gráfico da função.

O procedimento descrito pode ser usado para avaliar a função em qualquer outro valor de domínio. Por exemplo, você pode encontrar f (-2), f (100) ou mesmo f (h), onde h é um valor variável arbitrário, que pertence ao domínio da função.

Avalie uma função em um valor x = h 

Suponha que você queira avaliar a função em algum valor arbitrário, uma operação frequente no cálculo matemático.

Nesse caso, X é substituído por H, da mesma maneira que é feita quando X assume qualquer valor numérico, e o resultado é simplificado o máximo possível.

Quando a operação resultante não pode mais ser simplificada, a operação resultante é deixada.

Pode atendê -lo: Enegon: Propriedades, como fazer um Enegon, exemplos

Exemplo

Você deseja avaliar a função f (x) = x² - 3x - 4 em x = h+1. A abordagem necessária é a seguinte:

f (h+1) = (h+1)² - 3 ∙ (h+1) - 4

À direita da igualdade, o primeiro termo é um produto notável:

(H+1)² = h² +2h + 1

O termo a seguir é resolvido por meio de propriedades distributivas:

3 ∙ (h + 1) = 3h + 3

Ao substituir todas as opções acima, você tem:

f (h+1) = (h+1)² - 3 ∙ (h+1) - 4 = h² +2h + 1 - (3h + 3) - 4

Os termos semelhantes são reduzidos, por soma algébrica:

f (h+1) = h² + 2h + 1 - 3h - 3 - 4 = h² - H - 6

O quociente diferencial

O quociente diferencial ou razão de diferenças d de uma função f (x) é definido como:

Com a condição H ≠ 0, o que é necessário, pois a divisão por 0 não é definida.

Este quociente é interpretado geometricamente como a inclinação de uma linha secante para a curva, ou seja, uma linha que passa por dois pontos dela. As coordenadas desses pontos são: [x, f (x)] e [x+h; f (x+h)], como visto na figura a seguir:

O quociente diferencial é equivalente a calcular a inclinação da linha secante para a curva, que passa pelos pontos indicados. Fonte: Wikimedia Commons.

É por isso que esse quociente aparece no cálculo da derivada de uma função, uma vez que a abordagem “h” do valor 0, a linha secante tende a se tornar uma linha tangente no ponto (x, y), porque os pontos na interseção de A figura está tão próxima que eles tendem ao mesmo ponto.

Assim, a linha se torna tangente (intercepta a curva em um único ponto).

Esta é precisamente a definição de derivado de uma função: a inclinação da linha tangente à curva no ponto de coordenada (x, f (x))).

Pode servir a você: mídia ponderada: como é calculado, exemplos e exercícios

Como pode ser visto, o quociente diferencial requer avaliar a função em (x + h) e em x. Os exemplos a seguir ilustram como fazer isso.

Exemplo 1

Você deseja encontrar o quociente diferencial da função f (x) = 2x - 3. O primeiro passo é aumentar a avaliação da função para x = x + h, como este:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Então, o resultado é substituído na definição de D, dado anteriormente:

Com h ≠ 0.

O numerador é simplificado o máximo possível, reduzindo termos semelhantes:

Finalmente, os fatores comuns no numerador e denominador são simplificados:

D = 2

Exemplo 2

Encontre o quociente diferencial da função f (x) = x² - 3x - 4.

Procedemos como no exemplo anterior, encontrando o primeiro f (x+h), substituindo o resultado em d e simplificando o máximo:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2hx + h² - 3x - 3h - 4

= 2x+h-3

Portanto:

D = 2x+h-3

Onde h ≠ 0.

Exercícios resolvidos

Exercício 1

Avalie a função f (x) = 2x² - 4x + 1 quando:

a) x = -1
b) x = 0
c) x = 2

Solução para

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Solução b

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Solução c

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Exercício 2

Uma equipe conservacionista determinou que a função w (t) = 0.lt² + 1.8T serve para modelar a quantidade de resíduos "W", em quilogramas, que são jogados em um certo rio, em um tempo "T", dado em dias.

Calcule a quantidade de resíduos jogados no rio no final de:

a) 3 dias
b) 1 semana
c) 1 mês

Solução para

A função W (t) é avaliada em t = 3 dias:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kg

Solução b

Antes de avaliar, você deve passar de 1 a semana:

1 semana = 7 dias

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kg

Solução c

Novamente, é necessário transformar os meses em dias:

1 mês = 30 dias

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kg

Referências

1. Larson, r. 2012. Pré -cálculo. 8º. Edição. Cengage Learning.
2. Instituto Monterey. Avaliação de funções. Recuperado de: MontereyInstitute.org.
3. Stewart, J. 2007. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
4. Sullivan, m. 1997. Pré -cálculo. 4º. Edição. Pearson Education.
5. Zill, d. 2008. Preccultment com avanços de cálculo. 4º. Edição. McGraw Hill.