Espelho convexo

O que é um espelho convexo?

Ele espelho convexo Ou divergente é um espelho curvo, quase sempre esférico e com a superfície reflexiva no lado externo da esfera, como os ornamentos da árvore de Natal. Graças aos espelhos convexos, é possível.

Por exemplo, os espelhos que são colocados nas ruas para facilitar o trânsito dos veículos em cruzamentos estreitos são convexos, pois produzem uma imagem com um amplo campo visual.

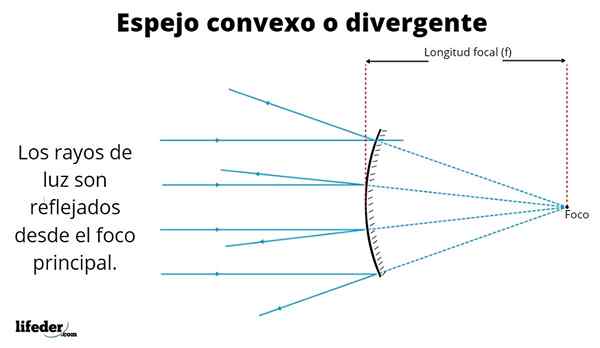
Ilustração de um espelho convexo

As imagens assim formadas são diversas, dependendo do local onde o objeto é colocado. A imagem superior mostra raios paralelos de uma fonte distante como o sol.

Os raios são refletidos de acordo com a lei de reflexão, que indica que o ângulo de incidência do raio é o mesmo com o qual é refletido. Como podemos ver, os raios refletidos são separados - eles não cruzam - quando deixam a superfície especular, e é por isso que esse tipo de espelho também é conhecido como divergente.

Quando as reflexões se estendem para trás do espelho - linhas descontínuas da figura - essas se cruzam em um ponto chamado foco.

Características dos espelhos convexos

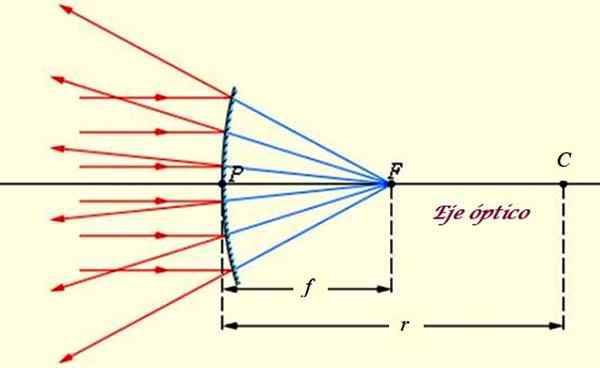Espelho convexo ou divergente, no qual os raios de uma fonte distante como o sol afetam. Fonte: f. Zapata.

O espelho convexo tem as seguintes características (ver Imagem Superior):

-Os pontos notáveis ​​do espelho são:

• C O centro, que coincide com o centro da esfera a que o espelho pertence.
• F Focus, onde os raios refletidos por trás do espelho convergem.
• O vértice p do mesmo, que corresponde ao centro da superfície esférica e é colineal com c e f.

Pode servir você: ÍO (satélite)

-Tem eixo óptico qualquer Eixo principal, que é a linha perpendicular à superfície especular. Os raios que afetam o eixo óptico são refletidos na mesma direção.

-O centro da esfera a que o espelho pertence está no ponto C e r é seu raio. Um C é conhecido como Centro de curvatura, enquanto que r é o Raio de curvatura e indica como o espelho é curvo: um menor r, Mais acentuado é a forma convexa.

-O ponto de interseção dos raios refletidos é conhecido como Ponto focal do espelho. A distância entre F e P é aproximadamente r/2:

F = r/2

Esta expressão é válida para espelhos cujo tamanho é muito menor que seu raio de curvatura.

-A imagem que se forma é menor e também virtual, pois está localizada atrás do espelho, como veremos a seguir.

Formação de imagem no espelho convexo

Saber como a imagem formada no espelho convexo é o tratamento de raios, que consiste em representar os raios de luz que saem do objeto através de linhas retas.

Esses raios são refletidos na superfície do espelho e os raios refletidos também são desenhados. O método do raio é aplicável a qualquer tipo de espelho, não apenas convexo.

Ao prolongar os raios refletidos, eles se cruzam em um determinado ponto, e é exatamente onde a imagem é formada. A extensão dos raios refletidos provenientes de um objeto estendido como uma árvore é mostrado na figura inferior por linhas descontínuas.

Na Figura inferior, três raios do objeto são desenhados, muito particulares e fáceis de desenhar, bem como suas reflexões:

Pode atendê -lo: dilatação térmica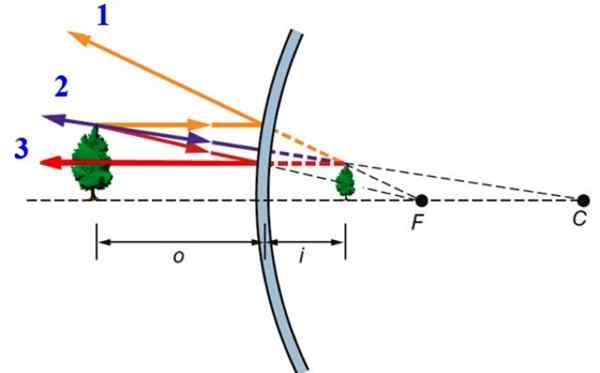 Figura 2.- Formação de imagem no espelho convexo. Fonte: f. Zapata.

-Ray 1, que afeta paralelo ao eixo óptico.

-Ray 2, que afeta a exolitação do raio refletido, passa precisamente através do foco do espelho, ou seja, ponto F. Este raio é refletido em paralelo ao eixo óptico.

-Finalmente, o raio 3, que atinge perpendicularmente a superfície esférica, e por esse motivo, é refletido na mesma direção.

Em princípio, este procedimento se aplica a cada ponto da árvore, mas com as informações obtidas dos três raios desenhados, é suficiente para encontrar a imagem do objeto: é formada atrás do espelho, é certo e menor que o original.

Exemplos e aplicações de espelhos convexos

Muitas superfícies esféricas muito puxadas atuam como espelhos convexos, por exemplo, enfeites de Natal brilhantes e prateados, bem como colheres de aço novas e brilhantes.

Os espelhos convexos também têm muitas aplicações práticas, por exemplo:

Espelhos para evitar acidentes de trânsito

Espelhos convexos em ruas e avenidas ajudam a evitar acidentes, pois eles permitem que você veja o tráfego que vem dos cantos.

Espelhos de vigilância

Nas lojas e bancos, geralmente existem espelhos convexos para detectar ladrões, bem como evitar colisões entre pessoas e veículos de empilhadeira que circulam nos corredores e entre as prateleiras.

Espelhos de vista traseira

Carros e motocicletas têm espelhos convexos, que produzem imagens um pouco menores, mas cobrem mais campo visual do que espelhos planos.

Telescópio CASSEGRAIN

Um dos espelhos do refletor de Cassegrain, o espelho secundário, é convexo, embora não seja esférico e serve para refletir a imagem em direção ao espelho principal do telescópio.

Pode servir a você: energia gravitacional: fórmulas, características, aplicações, exercícios

Equações espelhadas convexas

Considere os retângulos da figura a seguir, determinada pelo raio 1, que vem do topo da flecha, sua reflexão e a extensão deste.

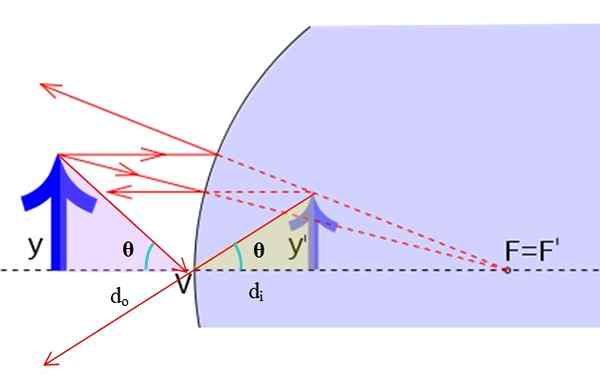Geometria para encontrar a ampliação do espelho. Fonte: f. Zapata.

A imagem original tem altura e, enquanto a altura da imagem virtual é e ' . É verdade que:

Tan θ = y/d_qualquer = Y '/d_Yo

Ampliação do espelho

A razão entre a altura da imagem e a altura do objeto é o ampliação do espelho, É chamado que, mesmo que a imagem obtida seja menor que o objeto real. Nós denotamos por m:

M = y '/ y = D_Yo /d_qualquer

Relação entre o objeto e sua imagem no espelho convexo

Agora, vamos considerar essa outra figura, onde a região da AVF pode ser considerada aproximadamente como um triângulo certo, uma vez que a curvatura do espelho não é muito pronunciada. Portanto:

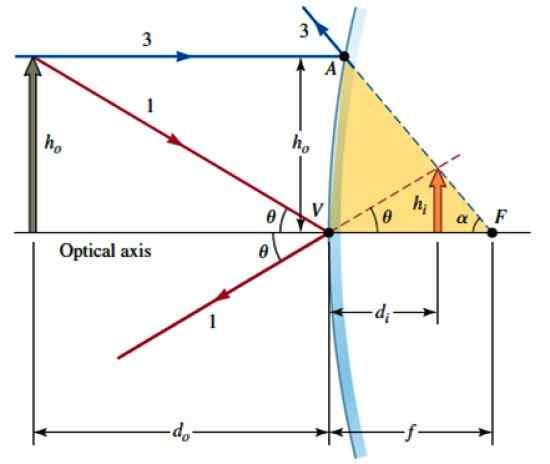Geometria para encontrar a relação matemática entre o objeto e sua imagem. Fonte: Katz, D. Física para cientistas e engenheiros.

Av ≈ h_qualquer

Então:

Tan α = h

Portanto:

O inverso desta expressão é a ampliação, então:

Portanto:

1- (d_Yo /f) = D_Yo /d_qualquer

Dividindo tudo entre D_Yo:

Finalmente:

 Agora, para espelhos, algumas convenções se aplicam. De fato, embora saibamos que uma distância é sempre positiva, a todas as distâncias por trás do espelho, elas são distinguidas com um sinal negativo.

Portanto, como F e d_Yo Eles estão atrás do espelho, são colocados menos sinais, enquanto para a distância d_qualquer Isso não é necessário, pois está à frente do espelho. Assim, a equação anterior permanece:

Pode -se demonstrar que esta equação também é válida para o espelho côncavo.

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 2. Mc Graw Hill.
2. Giambattista, a. 2010. Física. 2º. Ed. McGraw Hill.
3. Katz, d. 2017. Física para cientistas e engenheiros. Cengage Learning.
4. Thomas, w. 2008. Física conceitual. McGraw Hill.
5. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. McGraw Hill.