Determinação do equilíbrio de tradução, aplicações, exemplos

Ele Balanço translacional É um estado em que um objeto como um todo é quando todas as forças que atuam nele são compensadas, resultando em uma força vazia. Matematicamente, é equivalente a dizer que f₁+ F₂ +  F₃ +.. . = 0, sendo f₁, F₂,  F₃... as forças envolvidas.

O fato de um corpo estar em equilíbrio translacional não significa que ele está necessariamente em repouso. Este é um caso particular da definição anterior. O objeto pode estar em movimento, mas na ausência de aceleração, este será um movimento retilíneo uniforme.

figura 1. O equilíbrio de tradução é importante para um grande número de esportes. Fonte: Pixabay.

Então, se o corpo estiver em repouso continuar. E se você já tem movimento, terá uma velocidade constante. Em geral, o movimento de qualquer objeto é uma composição de traduções e rotações. As traduções podem ser como mostrado na Figura 2: linear ou curvilíneo.

Mas se um dos pontos do objeto for fixo, a única possibilidade de se mover é girar. Exemplo disso é um CD, cujo centro é fixo. O CD tem a possibilidade de girar em torno de um eixo que passa por esse ponto, mas não para se mover.

Quando objetos têm pontos fixos ou são suportados em superfícies, se fala de links. Os links interagem limitando os movimentos que o objeto é capaz de fazer.

[TOC]

Determinação do equilíbrio translacional

Para uma partícula em equilíbrio, é válido garantir que:

F_R = 0

Ou em notação resumida:

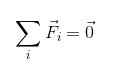
É claro que, para que um corpo esteja em equilíbrio translacional, as forças que agem nele devem ser compensadas de alguma forma, para que seu resultado seja anulado.

Dessa maneira.

Pode servir a você: Teoria do Big Bang: características, estágios, evidências, problemas

Agora, se os objetos podem girar, eles geralmente farão. É por isso que a maioria dos movimentos consiste em combinações de tradução e rotação.

Rotação de um objeto

Quando o balanço rotacional é importante, pode ser necessário garantir que o objeto não gire. Então você tem que estudar se há torques ou momentos agindo nele.

O torque é a magnitude do vetor da qual as rotações dependem. Exige que uma força seja aplicada, mas o ponto de aplicação disso também é importante. Para esclarecer a idéia, considere um objeto estendido no qual uma força age F E vamos ver se você é capaz de produzir uma rotação em relação a algum eixo ou.

Já está intitulado que empurrando o objeto no ponto P com a força F, É possível mudar o ponto O, com uma direção anti -hecome. Mas a direção em que a força é aplicada também é importante. Por exemplo, a força aplicada na figura do meio não será capaz de virar o objeto, embora certamente possa movê -lo.

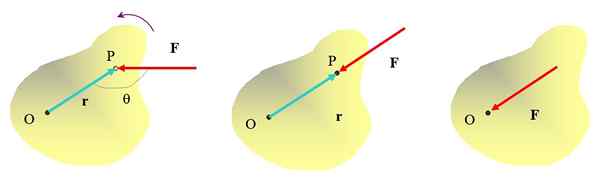Figura 2. Várias maneiras de aplicar uma força em um objeto extenso, somente na figura do extremo deixado um efeito de rotação é obtido. Fonte: Self feito.

Aplicar força diretamente no ponto ou não será usado para girar o objeto também. Então é claro que, para alcançar um efeito de rotação, a força deve ser aplicada a uma certa distância do eixo de rotação e sua linha de ação não deve passar por esse eixo.

Definição de torque

O torque ou o momento de uma força, indicado como τ de magnitude do vetor responsável por reunir todos esses fatos, é definido como:

τ = r x f

O vetor r É direcionado do eixo de rotação para o ponto de aplicação da força e a participação do ângulo entre R e F é importante. Portanto, a magnitude do torque é expressa como:

Pode atendê -lo: a primeira lei de Newton: fórmulas, experimentos e exercícios

τ = r.F.Sen q

O torque mais eficaz ocorre quando r e F Eles são perpendiculares.

Agora, se desejar que não haja rotações ou passam com aceleração angular constante, é necessário que a soma dos torques que atue no objeto seja nula, análoga ao que foi considerado para as forças:

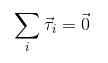
Condições de equilíbrio

Equilíbrio significa estabilidade, harmonia e equilíbrio. Para que o movimento de um objeto possua essas características, as condições descritas nas seções anteriores devem ser aplicadas:

1) f₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

A primeira condição garante o equilíbrio da tradução e o segundo a rotacional. Ambos devem ser cumpridos se o objeto for desejado permanecer em Equilíbrio estático (ausência de movimento de qualquer tipo).

Formulários

As condições de equilíbrio são aplicáveis ​​a inúmeras estruturas, pois quando edifícios ou objetos diversos são construídos, é feito com a intenção de que suas partes sejam mantidas nas mesmas posições relativas entre si. Em outras palavras, que o objeto não é desarmado.

Isso é importante, por exemplo, ao construir pontes que permanecem firmes sob seus pés ou ao projetar estruturas habitáveis ​​que não mudam de posição ou tendem a despejar.

Embora se acredite que o movimento retilíneo uniforme seja uma simplificação extrema do movimento, que geralmente ocorre pouco da natureza, deve -se lembrar que a velocidade da luz no vazio é constante e a do som no ar também, se considera homogêneo ao meio ambiente.

Em muitas estruturas móveis feitas pelo homem, é importante que uma velocidade constante seja mantida: por exemplo, em escadas mecânicas e linhas de montagem.

Pode servir a você: Segunda Lei da Termodinâmica: Fórmulas, Equações, Exemplos

Exemplos de equilíbrio de tradução

Este é o exercício clássico de tensões que mantêm a lâmpada em equilíbrio. Sabe -se que a lâmpada pesa 15 kg. Encontre as magnitudes das tensões necessárias para mantê -las nesta posição.

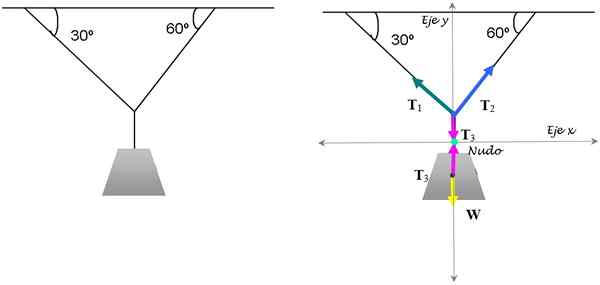Figura 3. O equilíbrio da lâmpada é garantido aplicando a condição de equilíbrio de tradução. Fonte: Self feito.

Solução

Para resolvê -lo, focamos no nó onde as três cordas se reúnem. Os respectivos diagramas do corpo livre para o nó e a lâmpada são mostrados na figura acima.

O peso da lâmpada é W = 5 kg . 9.8 m/s² = 49 n. Para que a lâmpada esteja em equilíbrio, basta que a primeira condição de equilíbrio seja atendida:

T₃ - W = 0

T₃ = W = 49 n.

Tensões T₁ e T₂ Eles devem se decompor:

T_1y + T_{2 e} - T₃ = 0 (Verão das forças ao longo do eixo y))

-T_1x +T_2x = 0 (Verão das forças ao longo do eixo X)

Aplicando trigonometria:

T₁.Cos 60º +t₂ .Cos 30º = 49

- T₁.Sen60º +t₂.Sen30º = 0

É um sistema de duas equações com duas incógnitas, cuja resposta é: T₁ = 24.5 n e T₂ = 42.4 n.

Referências

1. Rex, a. 2011. Fundamentos da Física. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7^MA. Ed. Cengage Learning. 120 - 124.
3. Serway, r., Vulle, c. 2011. Fundamentos da Física. 9^{n / D} Ed. Cengage Learning. 99-112.
4. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Física. Addison Wesley. 332 -346.