Balanço de tradução Condições, exemplos, exercícios

Afirma -se que um objeto está em Balanço de tradução Quando a soma das forças que agem sobre ele é zero. Isso não significa que exista necessariamente o resto, mas o movimento, se existente, seria uniforme ou exclusivamente retilíneo rotacional, em caso de ser um objeto extenso.

As condições de equilíbrio mecânico são baseadas nas leis de Newton sobre mecânica. De fato, a primeira lei nos diz que um objeto está em repouso ou se move com um movimento retilíneo uniforme, desde que nenhuma força líquida age sobre ele.

Este poste de luz está em equilíbrio de tradução

Agora, a força líquida ou força resultante é simplesmente a soma vetorial de todas as forças que agem no objeto. De acordo com a segunda lei de Newton, essa soma deve ser igual ao produto entre massa e aceleração, mas se o objeto não for acelerado, esta soma será anulada.

E como não há aceleração são as duas possibilidades mencionadas: o corpo está em repouso, ou seja, não se move, ou se isso acontecer, tem que estar com MRU. No primeiro caso, há falar sobre o equilíbrio transnacional estático e, no segundo, dinâmico.

O equilíbrio da tradução é um fator importante em muitos aspectos da engenharia, por exemplo, na construção. Os elementos que compõem um edifício: vigas, cabos, molduras e muito mais, devem estar em equilíbrio para garantir a estabilidade do gabinete.

O equilíbrio da tradução também é procurado em estruturas móveis, como escadas mecânicas, bandas de transporte e na prática de vários esportes.

[TOC]

Condição do equilíbrio da tradução

Suponha que várias forças atuem em um corpo, que denotamos como F₁, F₂, F₃.. . F_n, usando uma letra ousada para destacar o fato de que as forças são vetores e devem ser adicionadas como tal.

A soma vetorial de todas essas forças é chamada força resultante qualquer Força resultante. Se esta soma resultar no vetor nulo, a condição para o saldo da tradução será cumprida:

Pode atendê -lo: circuito elétrico fechado

F₁+ F₂+ F₃.. .+ F_n = 0

Esta condição pode ser escrita de forma compacta usando o resumo:

∑ F_Yo = 0

Em termos dos componentes da força resultante, a equação anterior, que é vetorial, pode ser dividida em três equações escalares, uma para cada componente da força resultante:

∑ f_Ix = 0; ∑ f_e = 0 e ∑ f_z = 0

Na prática, não é fácil.

Esta é a razão pela qual objetos reais quase nunca estão isentos de forças externas e, como conseqüência, é difícil obter o equilíbrio da tradução.

Portanto, os engenheiros usam mecanismos para reduzir o fricção, como rolamentos e o uso de óleos de lubrificante.

Diagramas do corpo livre

O diagrama do corpo livre é um esquema no qual as forças que agem no corpo são desenhadas. Quando o equilíbrio da tradução é procurado, essas forças devem ser equilibradas. Por exemplo, se você está agindo uma força vertical direcionada para baixo, como peso, deve haver uma força vertical que tenha exatamente a mesma magnitude.

Essa força pode ser fornecida pela mão que suporta o objeto para que não caia, uma corda ou simplesmente a superfície de uma tabela.

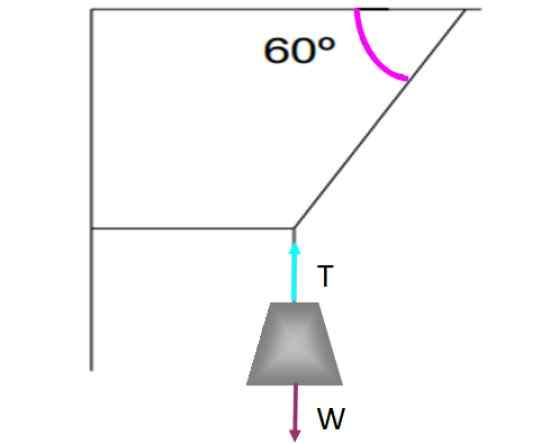
Se houver uma força tangencial à superfície, como atrito cinético ou estático, deve haver outra força oposta para que o equilíbrio exista. Por exemplo, vamos observar o peso que pendura nas cordas mostradas na figura a seguir.

Exemplo de um objeto que está em equilíbrio de tradução, isso pesa sujeito ao teto usando as cordas dispostas como mostrado na imagem. Fonte: f. Zapata.

O peso permanece em equilíbrio de tradução e sem movimento, graças à corda vertical que o mantém exercendo uma tensão T que compensa o peso C. Cada força foi representada no oeste através de uma flecha, cada um de tamanho igual e com a mesma direção, mas a direção oposta.

Pode servir a você: Processo isobárico: fórmulas, equações, experimentos, exercícios

A força de equilíbrio

Suponha que um conjunto de forças age em um objeto. Isso é chamado de um Sistema de Forças dos quais o resultante pode ser encontrado como explicado acima: adicionar cada sistema forças do sistema.

Bem, pela força oposta a este resultado, é chamada força de equilíbrio. Se a força resultante for F_R E a força de equilíbrio é E, então:

E + F_R = 0

Portanto:

E = - F_R

Exemplos de equilíbrio de tradução

Muitos objetos que encontramos diariamente, dentro e fora de casa, estão em equilíbrio de tradução:

Edifícios e estradas

Edifícios e estradas são construídos para permanecer estável e não girar ou desmoronar. No entanto, em arranha -céus e em geral edifícios muito altos, é necessária alguma flexibilidade para resistir à ação do vento.

Livros e objetos nas prateleiras

Livros em uma biblioteca e produtos em lojas são objetos que permanecem em equilíbrio de tradução e sem se mover.

A mobília

Os móveis, a TV de tela plana e as pinturas na parede, bem como as lâmpadas penduradas no teto, para mencionar alguns objetos, estão em equilíbrio de tradução.

Os semáforos

Os semáforos são presos por postes e cabos, para que eles não caam. No entanto, sabemos que o vento os faz oscilar.

A iluminação pública

As luzes de iluminação pública também estão em equilíbrio de tradução, fixadas em postes leves, como a imagem principal da imagem principal.

Exercício resolvido

Que magnitude deve ter a força F_s atrito estático para a caixa na figura permanecer em repouso no meio do plano inclinado Um ângulo α de 37º? A massa da caixa é m = 8 kg.

Pode atendê -lo: API Gravity: escala e classificação do petróleo bruto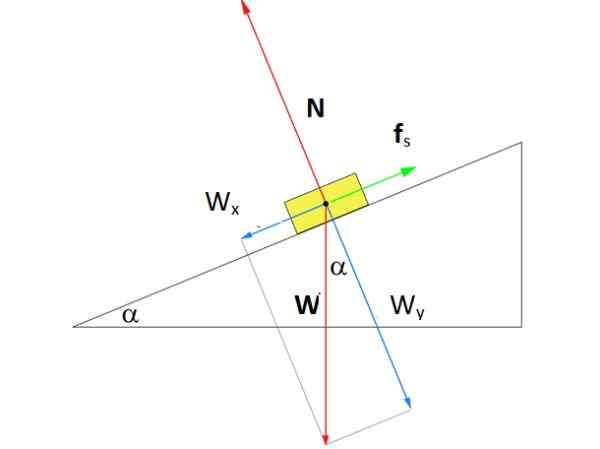Diagrama do corpo livre para um objeto de repouso em um plano inclinado. Fonte: f. Zapata.

Solução

A figura mostra o diagrama do corpo livre no avião. Existem três forças agindo nela: o peso C, direcionado verticalmente para baixo, o normal N, que é a força perpendicular exercida pela superfície do plano sobre a caixa e, finalmente, a força de atrito estático F_s que se opõe à caixa para escorregar ladeira abaixo.

A condição de equilíbrio de tradução estabelece que:

C + N + F_s = 0

Mas você deve se lembrar de que essa é uma soma vetorial e, para executá -la, é necessário decompor as forças em componentes ao longo dos eixos de coordenadas.

Na figura, foi desenhado um sistema de coordenadas no qual o eixo x corre paralelo à superfície do plano inclinado. Com essa escolha, o atrito estático cai nesse eixo, enquanto o normal está no eixo e. O peso é a única força inclinada e devemos decompor com a ajuda da trigonometria:

C_x = W. sin α
C_e = W. cos α

A soma das forças ao longo de cada eixo é:

∑ f_e = N - w_e = 0
∑ f_x = f_s - C_x = 0

A partir desta última equação, segue -se que:

F_s = W_x

E como w_x = W. sin α e a magnitude do peso, por sua vez, é w = m.g, sendo g o valor da gravidade, então a magnitude do toque estático é simplesmente:

F_s = m⋅g⋅sen α = 8 kg × 9.8 m/s² × sen 37º = 47.2 n.

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 2. Dinâmico. Editado por Douglas Figueroa (USB).
3. Giambattista, a. 2010. Física. 2º. Ed. McGraw Hill.
4. Serway, r., Jewett, J. (2008). Física para Ciência e Engenharia. Volume 1. 7^MA. Ed. Cengage Learning.
5. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. McGraw Hill.