Características de energia potencial, tipos, cálculo e exemplos

O energia potencial É a energia que os corpos têm em sua configuração. Quando os objetos interagem, existem forças capazes de fazer o trabalho, e essa capacidade de fazer o trabalho, que é armazenada na disposição que eles têm, podem se traduzir em energia.

Por exemplo, os seres humanos aproveitaram a energia potencial da água que cai desde os tempos imemoriais, as primeiras fábricas giratórias e depois em usinas hidrelétricas.

Cataratas do Niágara: uma enorme reserva de energia potencial gravitacional. Fonte: Pixabay.

Por outro lado, muitos materiais têm uma capacidade notável de fazer o trabalho deformando e depois retornando ao seu tamanho original. E em outras circunstâncias, o arranjo da carga elétrica permite armazenar energia potencial elétrica, como em um condensador.

A energia potencial oferece muitas possibilidades para se transformar em outras formas úteis de energia, daí a importância de conhecer as leis que a governam. 

[TOC]

Origem da energia potencial

A energia potencial de um objeto tem sua origem nas forças que o afetam. No entanto, a energia potencial é uma magnitude escalar, enquanto as forças são vetoriais. Portanto, para especificar a energia potencial, é suficiente para indicar seu valor numérico e as unidades selecionadas.

Outra qualidade importante é o tipo de força com que a energia potencial pode ser armazenada, pois nenhuma força tem essa virtude. Somente as forças conservadoras armazenam energia potencial nos sistemas em que eles agem.

Uma força conservadora é aquela para a qual o trabalho não depende da trajetória seguida pelo objeto, mas apenas do ponto de partida e do ponto de chegada. A força que impulsiona a queda de água é a gravidade, que é uma força conservadora.

Por outro lado, forças elásticas e eletrostáticas também possuem essa qualidade; portanto, há energia potencial associada a elas.

Forças que não atendem ao requisito acima mencionado, são chamadas de não -conservadoras; Exemplo deles está em atrito e resistência ao ar.

Tipos de energia potencial

Como a energia potencial sempre deriva de forças conservadoras, como as já mencionadas, se fala em energia potencial gravitacional, energia potencial elástica, energia potencial eletrostática, energia potencial nuclear e energia química potencial de energia.

Energia potencial gravitacional

Qualquer objeto tem energia potencial com base na altura que tem em relação ao solo. Esse simples fato de aparência ilustra porque a cachoeira é capaz de aumentar as turbinas e eventualmente se transformada em eletricidade. O exemplo dos esquiadores mostrados aqui também mostra a relação de peso e altura com energia potencial gravitacional.

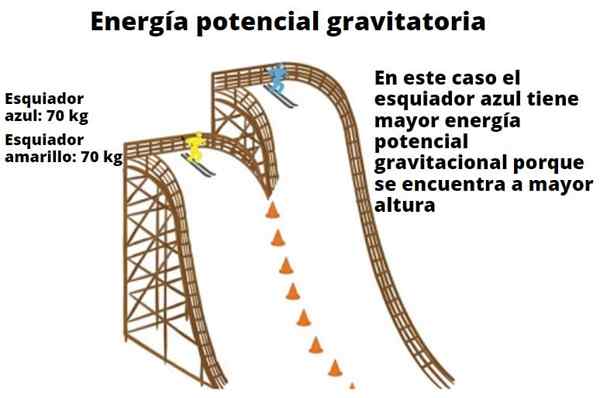
Outro exemplo é o de um carro da montanha, que tem maior energia potencial quando está em uma certa altura no solo. Uma vez atingido o nível do piso, sua altura é igual a zero e toda a sua energia potencial foi transformada em energia cinética (energia de movimento).

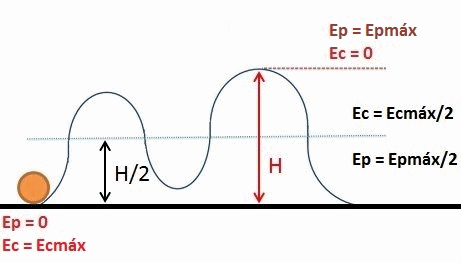A animação mostra a troca entre energia potencial gravitacional e energia cinética, de um objeto que se move em uma montanha -russa. A soma de ambas as energias, chamada energia mecânica, é constante ao longo do movimento. Fonte: Wikimedia Commons.

Energia potencial elástica

Objetos como molas, arcos, bestas e ligas são capazes de armazenar energia potencial elástica.

Quando o arco está tenso, o goleiro faz um trabalho que é armazenado como energia potencial do sistema arco-fet. Quando o arco é lançado, essa energia é transformada em movimento da flecha. Fonte: Pixabay.

A elasticidade de um corpo ou material é descrita pela lei de Hooke (até certos limites), que nos diz que a força capaz de se esforçar quando comprimida ou esticada é proporcional à sua deformação.

Pode servir a você: Ferromagnetismo: Materiais, Aplicações e Exemplos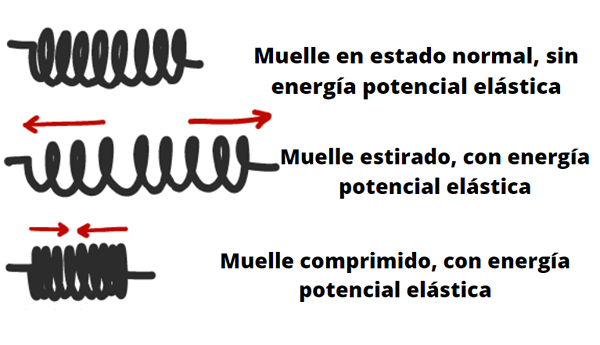

Por exemplo, em caso de primavera ou primavera, isso significa que quanto mais ele encolhem ou se estende, maior a força que pode ser exercida em um objeto colocado em uma extremidade.

Energia potencial eletrostática

É a energia que as cargas elétricas têm sob sua configuração. As cargas elétricas do mesmo sinal são repelidas, para colocar algumas cargas positivas - ou negativas - em uma determinada posição, um agente externo deve fazer o trabalho. Caso contrário, eles tenderiam a se separar.

Este trabalho é armazenado na maneira como as cargas foram localizadas. Quanto mais próximos as cargas do mesmo sinal são, maior a energia potencial que a configuração terá. Isso acontece pelo contrário quando se trata de diferentes sinais de cargas; Enquanto eles atraem, quanto mais próximos eles estão, menos energia potencial eles têm.

Energia potencial nuclear

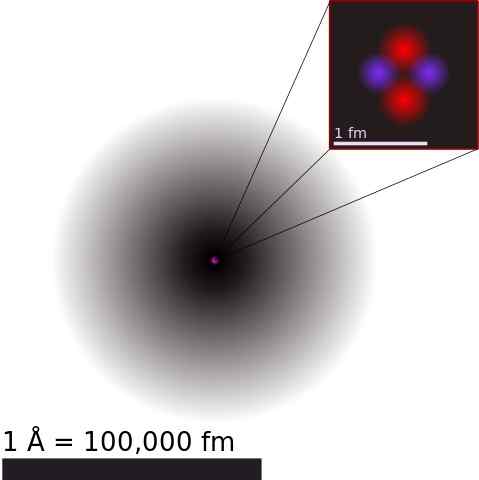Átomo de hélio aproximado. No núcleo, os prótons são representados em vermelho e os nêutrons em azul.

O núcleo atômico é composto por prótons e nêutrons, genericamente chamados Nucleonas. Os primeiros têm carga elétrica positiva e os últimos são neutros.

Como eles são aglomerados em um pequeno espaço além da imaginação, e sabendo que as cargas do mesmo sinal são repelidas, vale a pena perguntar como o núcleo atômico permanece coesão.

A resposta está em outras forças, além da repulsão eletrostática, típica do núcleo, como interação nuclear forte e interação nuclear fraca. Essas são forças muito intensas, que excedem em muito a força eletrostática.

Energia potencial química

Esta forma de energia potencial vem de como as moléculas de átomos e substâncias estão disponíveis, de acordo com os diferentes tipos de ligações químicas.

Quando uma reação química é dada, essa energia pode ser transformada em outros tipos, por exemplo, por uma bateria elétrica ou bateria.

Exemplos de energia potencial

A energia potencial está presente na vida cotidiana em muitos aspectos. Observar seus efeitos é tão fácil quanto colocar qualquer objeto a uma certa altura e ter a certeza de que ele pode rolar ou cair a qualquer momento.

Aqui estão algumas manifestações dos tipos de energia potencial descritos anteriormente:

-Montanhas-russas

-Carros ou bolas rolando ladeira abaixo

-Arcos e flechas

-Baterias elétricas

-Um pêndulo de relógio

Quando uma das esferas extremas é acionada, o movimento é transmitido aos outros. Fonte: Pixabay.

-Balançar em um balanço

-Earra

-Use uma caneta retrátil.

Veja: Exemplos de energia potencial.

Cálculo de energia potencial

A energia potencial depende do trabalho que faz força e isso, por sua vez, não depende da trajetória, então pode -se afirmar que:

-Se A e B são dois pontos, o trabalho C_Ab  necessário ir de A a B, é igual ao trabalho necessário para ir de B para um. Portanto: C_Ab = W_BA, assim que:

C_Ab + C_BA = 0

-E se duas trajetórias diferentes 1 e 2 forem testadas para se juntar a esses pontos A e B, o trabalho realizado nos dois casos também é o mesmo:

 C₁ = W₂.

De qualquer forma, o objeto experimenta uma mudança na energia potencial:

Mudança = energia potencial final - energia potencial inicial

ΔU = u_final - OU_inicial = U_B - OU_PARA

Bem, a energia potencial do objeto é definida como o negativo do trabalho realizado pela força (conservador):

Δu = -w_Ab

Mas como o trabalho é definido por esta integral:

Pode atendê -lo: os 31 tipos de força na física e suas características

Onde F e dr (com negrito ou flecha) são respectivamente os vetores de força e deslocamento. Com isso em mente, a mudança na energia potencial é o negativo desta integral:

Para forças conservadoras como descritas, a integral é facilmente calculada. 

Observe que as unidades de energia potencial são as mesmas que as do trabalho. No sistema internacional se a unidade for o joule, que é abreviado e equivalente a 1 newton x metrô, pelo físico inglês James Joule (1818-1889).

Outras unidades de energia incluem o ergio no sistema CGS, o pé x pé de pé x pé, o BTU (Unidade Térmica Britânica), Calorias e Kilowatt-Hora.

Vamos ver alguns casos específicos de como calcular a energia potencial.

Cálculo da energia potencial gravitacional

Nas proximidades da superfície da Terra, a força da gravidade aponta verticalmente para baixo e sua magnitude é dada pela equação Peso = massa x gravidade.

Denotando o eixo vertical com a letra "y" e atribuindo a este endereço o vetor da unidade J, positivo e negativo, a mudança na energia potencial quando um corpo se move de y = y_PARA até y = y_B é:

Onde m representa o corpo do corpo e g O valor da aceleração da gravidade. Se você é escolhido e_PARA = 0 Como um nível de referência no solo, no qual u é corrigido como 0, você tem:

U (y) = mGy

Cálculo da energia potencial elástica

A lei de Hooke nos diz que a força é proporcional à deformação:

F = -k.x

Aqui x É a deformação e k É uma constante da primavera, o que indica o quão rígido é. Através dessa expressão, a energia potencial elástica é calculada, levando em consideração que Yo É o vetor de unidade na direção horizontal:

Ao escolher OU_PARA = 0 em  x_PARA, A expressão anterior é a função U (x) Para a energia potencial da primavera:

U (x) = ½ kx²

Cálculo de energia potencial eletrostática

Quando você tem uma carga elétrica pontual, produz um campo elétrico que percebe outra carga pontual q, E o que funciona nele ao passar de uma posição para outra no meio do campo. A força eletrostática entre duas cargas específicas tem direção radial, simbolizada através do vetor de unidade r:

 Aqui k_e É a constante eletrostática ou constante de Coulomb, cujo valor é k_e ≈ 9 x 10⁹  N.m² /C² Nas unidades de sistema internacional. Segue que:

 Selecionando u = 0 quando r_PARA → ∞, permanece:

Exercícios resolvidos

- Exercício 1: uma primavera que se estende

Uma primavera cuja constante é k = 10.0 N/cm inicialmente se estende 1.00 cm do seu comprimento de equilíbrio. É solicitado para calcular a energia adicional necessária para esticar a mola até 5.00 cm além do seu comprimento de equilíbrio.

Solução 

Substituindo diretamente x = 1.00 cm na equação para u (x).CM, mas os centímetros devem se tornar medidores para obter energia em Joules:

U (1) = 0.5 x 10.0 n/cm x (1.00 cm)² = 5 n. cm = 0.05 J; U (5) = 0.5 x 10.0 N/cm x (5.00 cm)² = 125 n.cm = 1.25 J

Portanto, a diferença de energia procurada é 1.25 - 0.05 J = 1.20 j.

- Exercício 2: Forças Conservadoras e Não Conservativas

Um pequeno bloco do ponto A é liberado do repouso, para que deslize ao longo da rampa curva sem atrito para o ponto B. A partir daí, entra em uma longa superfície horizontal áspera, com um coeficiente de atrito dinâmico μ_k = 0.2. Encontre a que distância do ponto B para, assumindo que H_PARA= 3m.

Pode servir a você: Barrada Galáxia Espiral: Formação, Evolução, Características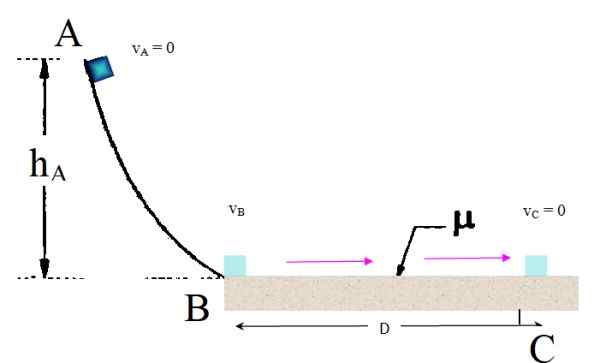Figura por exemplo 1. Fonte: f. Zapata.

Solução 

Quando o bloco está em uma altura h_PARA Em relação ao piso, tem energia potencial gravitacional devido à sua altura. Ao deixar ir, essa energia potencial gradualmente se torna energia cinética e, à medida que desliza pela rampa curva suave, sua velocidade está aumentando.

Durante a viagem de A a B, as equações do movimento retilíneo uniformemente variado não podem ser aplicadas. Embora a gravidade seja responsável pelo movimento do bloco, o movimento que essas experiências são mais complexas, porque a trajetória não é retilínea.

Conservação de energia na rota AB

No entanto, como a gravidade é uma força conservadora e na rampa não há atrito, a conservação da energia mecânica pode ser usada para encontrar a velocidade quando atingir o final da rampa:

Energia mecânica em A = energia mecânica em B

m.g.h_PARA + ½ m.v_PARA² = m.g.h_B + ½ m.v_B²

A expressão é simplificada ao perceber que a massa aparece em cada termo. É liberado de Rest V_PARA = 0. E h_B Está no nível do solo, h_B = 0. Com essas simplificações, a expressão é reduzida para:

v_B² = Gh_PARA

Trabalho realizado esfregando na seção BC

Agora o bloco começa sua rota na seção aproximada com essa velocidade e finalmente para no ponto C. Portanto v_C = 0. A energia mecânica não é mais preservada, porque o atrito é uma força dissipativa, que fez um trabalho no bloco dado por:

C_tocar = -Frue de atrito x distância percorrida

Este trabalho tem um sinal negativo, já que o atrito cinético diminui o objeto, opondo -se ao seu movimento. A magnitude do atrito cinético F_k  é:

F_k = μ_k .N

Onde n é a magnitude da força normal. A força normal é exercida pela superfície no bloco e, como a superfície é totalmente horizontal, pois equilibra o peso P = mg, Portanto, a magnitude do normal é:

N = mg

O que leva a:

F_k = μ_k .mg

O trabalho que F_k Faz o bloco é: C_k = - f_k .D =- μ_k .mg.D.

Cálculo da mudança na energia mecânica

Este trabalho é equivalente à mudança de energia mecânica, calculada assim:

Energia mecânica em C - energia mecânica em b =

ΔE_m = (U_C +K_C)- (OU_B + K_B) = - μ_k .mg.D

Nesta equação, existem alguns termos que são anulados: k_C = 0, já que o bloco para em C e também é anulado_C = U_B, Por ser esses pontos no nível do solo. Simplificação Resultados em:

- K_B = - μ_k .m.g.D

½ m.v_B² = μ_k .m.g.D

A massa é cancelada novamente e pode ser obtida da seguinte forma:

D = (½ V_B²)/(μ_k . G) = (½ V_B²)/(μ_k . g) = (½g.h_PARA)/(μ_k . g) = (½h_PARA)/μ_k = 0.5 x 3 m / 0.2 = 7.5m

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 2. Dinâmico. Editado por Douglas Figueroa (USB).
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia. Pearson. 
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1-2.