Unidades de energia livre de Gibbs, como é calculado, exercícios resolvidos

O Energia livre de Gibbs (comumente chamado G) é um potencial termodinâmico definido como a diferença na entalpia H, exceto o produto da temperatura t, pela entropia S do sistema:

G = h - t s

A Gibbs Free Energy é medida em Joules (de acordo com o sistema internacional), em Ergios (para o Sistema de Unidades da Liga), em Calorias ou Electron Volts (Para electro volts).

figura 1. Diagrama mostrando a definição de energia Gibbs e seu relacionamento com os outros potenciais termodinâmicos. Fonte: potência nuclear.líquido.

Nos processos que ocorrem a pressão e temperatura constantes, a variação da energia livre de Gibbs é ΔG = ΔH - T ΔS. Em tais processos, (g) representa a energia disponível no sistema que pode se tornar trabalho.

Por exemplo, em reações químicas exotérmicas, a entalpia diminui enquanto a entropia aumenta. No Gibbs, funcionam, esses dois fatores são neutralizados, mas somente quando a energia de Gibbs diminui a reação ocorre espontaneamente.

Portanto, se a variação de g é negativa, o processo é espontâneo. Quando a função Gibbs atinge seu mínimo, o sistema atinge um equilíbrio estável. Em resumo, em um processo para o qual a pressão e a temperatura permanecem constantes, podemos afirmar:

- Se o processo for espontâneo, então ΔG < 0

- Quando o sistema está em equilíbrio: ΔG = 0

- Em um processo não espontâneo, aumenta: ΔG> 0.

[TOC]

Como é calculado?

A energia livre de Gibbs (G) é calculada pela definição dada no início:

G = h - t⋅s

Por sua vez, a entalpia H é um potencial termodinâmico definido como:

H = u + P V

- Passo a passo

Em seguida, será feita uma análise de etapa -para conhecer as variáveis ​​independentes das quais a energia Gibbs é uma função:

1- Da primeira lei da termodinâmica, a energia interna está relacionada à entropia do sistema e seu volume V para processos reversíveis por meio do relacionamento diferencial:

Pode servir a você: brometo de etídio: estrutura, propriedades, usos, toxicidade

DU = DQ - DW = TDS - PDV

A partir desta equação, segue -se que a energia interna u é uma função das variáveis ​​S e V:

U = u (s, v)

2- A partir da definição de H e a tomada do diferencial: é obtido:

dh = du + d (p v) = du + vdp + pdv

3- Substituindo a expressão por DU obtida em (1) você deve::

Dh = tds - pdv + vdp + pdv = tds + vdp

A partir daqui, conclui -se que a entalpia H depende da entropia S e da pressão P, ou seja::

H = h (s, p)

4- Agora é calculado o diferencial total de energia livre de Gibbs: obtendo:

Dg = dh -tds -sdt = tds + vdp -tds -sdt

Onde DH foi substituído pela expressão encontrada em (3).

5- Finalmente, simplificando, você recebe: DG = VDP - SDT, É claro que a energia livre g depende da pressão e da temperatura T como:

G = g (p, t)

- Relacionamentos termodinâmicos de Maxwell

A partir da análise na seção anterior, segue -se que a energia interna de um sistema é uma função de entropia e volume:

U = u (s, v)

Então o diferencial de OU ser:

du = ∂_SU |_V Ds + ∂_VU |_S DV = TDS - PDV

A partir dessa expressão em derivados parciais, as relações termodinâmicas de maxwell e assim portadas podem ser deduzidas. Os derivados parciais se aplicam quando uma função depende de mais de uma variável e é facilmente calculada aplicando o teorema da seção a seguir.

O primeiro relacionamento de Maxwell

 ∂_VT |_S = -Mon_SP |_V 

Para chegar a este relacionamento, o Teorema da Clairaut - Schwarz em derivados parciais, que afirma o seguinte:

"A segunda ordem derivados misturados com as variáveis ​​trocadas são as mesmas, desde que as funções a serem derivadas sejam contínuas e diferenciáveis".

Segundo relacionamento de Maxwell

A partir do que foi demonstrado no ponto 3 da seção anterior:

Pode atendê -lo: fatores que afetam a solubilidade

H = h (s, p) e dh = tds + vdp

Pode ser obtido:

 ∂_PT |_S = ∂_SV |_P 

Prosseguir de uma maneira semelhante com a Gibbs Free Energy G = g (p, t) E com a energia livre de Helmholtz F = f (t, v) Para obter as outras duas relações termodinâmicas de Maxwell. 

Figura 2. Josiah Gibbs (1839-1903) foi um físico, químico e matemático americano que fez grandes contribuições para a termodinâmica. Fonte: Wikimedia Commons.

Os quatro relacionamentos termodinâmicos de Maxwell 

1- associado à energia interna u: ∂_VT |_S = -Mon_SP |_V

2- aquele obtido da entalpia H: ∂_PT |_S = ∂_SV |_P 

3- Relacionado à energia de Helmholtz F: ∂_TP |_V = ∂_VS |_T 

4- ligado à energia livre de Gibbs G: ∂_TV |_P = -Mon_PS |_T

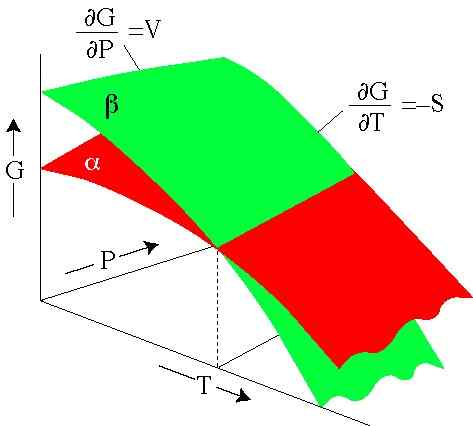Figura 2. A energia de Gibbs depende da pressão e temperatura. Cada superfície representa uma fase. (Serc.Carleton.Edu)

Exercícios resolvidos

Exercício 1

Calcule a variação da energia livre de Gibbs para 2 moles de gás ideal a uma temperatura de 300k durante uma expansão isotérmica que leva ao sistema de volume inicial de 20 litros a um volume final de 40 litros.

Solução

Lembrar a definição de energia livre de Gibbs é:

G = h - t s

Então uma variação finita de F será:

ΔG = ΔH - T ΔS, Desde Δt = 0

Em gases ideais, a entalpia depende apenas de sua temperatura absoluta, mas como é um processo isotérmico, então ΔH = 0 e ΔG = - T ΔS.

Para gases ideais, a variação de entropia de um processo isotérmico é: 

ΔS = nr ln (V₂/V₁)

Que se aplica ao caso deste exercício que temos:

ΔS = 2 moles x 8.314 j/(k mol) x ln (40l/20l) = 11,53 j/k

Então podemos obter a mudança na energia de Helmholtz:

ΔG = - 300k x 11,53 J/k = -3457,70 j.

Exercício 2

Levando em consideração que a energia livre de Gibbs é uma função da temperatura e pressão g = g (t, p); Determine a variação de g durante um processo em que a temperatura não muda (isotérmica) para n moles de um gás monoatômico ideal.

Pode atendê -lo: hidróxido de estrôncio (sr (oh) ₂)

Solução

Como demonstrado acima, a mudança na energia de Gibbs depende apenas da mudança de temperatura t e do volume V; portanto, uma variação infinitesimal é calculada de acordo com:

DG = -SDT + VDP

Mas se for um processo em que a temperatura é constante, df = + VDP, portanto, uma variação finita da pressão ΔP leva a uma mudança na energia de Gibbs dada por:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Usando a equação de gás ideal:

P V = n r t

Durante um processo isotérmico, acontece que:

D (P V) = P dv + V dp = 0

Quer dizer que:

dp/p = - dv/v

Portanto, o resultado anterior pode ser escrito dependendo da variação de volume ΔV:

Δg = + ∫ vdp = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (ΔV)

Exercício 3

Considerando a seguinte reação química:

N₂0 (g) + (3/2) ou₂ (g) ↔️no₂ (g) à temperatura t = 298 K

Encontre a variação da energia livre de Gibbs e, através do resultado obtido, indique se é ou não um processo espontâneo.

Solução

Abaixo das etapas:

- Primeiro passo: entalpias de reação

ΔHR = 2*ΔH (NO₂ (g)) - ΔH (n₂0 (g)) = 2*33.2-81.6 = -15.2kj/mol

- Segundo passo: a variação de entropia da reação

ΔSR = 2*s (não₂ (g)) - s (n₂0 (g)) - (3/2) s (ou₂ (g)) = 2*240.1 - 220.1 - 1,5*205.2 = -47,7 J/(mol*k).

- Terceira etapa: variação na função Gibbs

Este valor determinará o equilíbrio entre a diminuição da energia e o aumento da entropia para saber se a reação é finalmente espontânea ou não.

Δgr = Δhr -t ΔSr = -15,2 -298*(-47,7) = -985,4 j/mol

Como é uma variação negativa da energia de Gibbs, pode -se concluir que é uma reação espontânea à temperatura de 298 K = 25 ºC.

Referências

1. Castaños e. Exercícios de energia livre. Recuperado de: Lidiaconlachimica.WordPress.com.
2. Cengel, e. 2012. Termodinâmica. 7ª edição. McGraw Hill.
3. Librettexts. Energia livre de Gibbs. Recuperado de: química.Librettexts.org
4. Librettexts. O que são energia livre. Recuperado de: química.Librettexts.org
5. Wikipedia. Energia livre de Gibbs. Recuperado de: é.Wikipedia.com
6. Wikipedia. Energia livre de Gibbs. Recuperado de: em.Wikipedia.com