Fórmula de energia eletromagnética, equações, usos, exemplos

O Energia eletromagnética É aquele que se espalha pelas ondas eletromagnéticas (EM). Exemplo disso são a luz solar que irradia calor, a corrente que é extraída da saída elétrica e a que os raios X precisam produzir radiografias.

Como ondas sonoras quando fazem o tímpano vibrar, ondas eletromagnéticas são capazes de transferir energia que mais tarde pode se tornar calor, correntes elétricas ou diversos sinais.

figura 1. Antenas são necessárias em telecomunicações. Os sinais com os quais trabalham têm energia eletromagnética. Fonte: Pixabay.

A energia eletromagnética se propaga tanto em um ambiente de material quanto de vazio, sempre na forma de uma onda transversal, e fazer uso dela não é algo novo. A luz solar é a principal fonte de energia eletromagnética e a mais antiga conhecida, mas usar eletricidade é um pouco mais recente.

Foi apenas em 1891 quando Edison Company Coloque em operação a primeira instalação elétrica na Casa Branca em Washington DC. E que, como complemento, as luzes baseadas em gás que eram usadas na época, porque a princípio havia ceticismo suficiente em termos de uso.

A verdade é que até, nos lugares mais remotos e sem quentes, a energia eletromagnética que chega sem parar do espaço continua continuamente a manter a dinâmica que chamamos de casa no universo.

[TOC]

Fórmula e equações

Ondas eletromagnéticas são ondas transversais, nas quais o campo elétrico E e o campo magnético B Eles são perpendiculares um ao outro, sendo também a direção de propagação da onda perpendicular aos campos.

Todas as ondas são caracterizadas por sua frequência. É a ampla gama de frequências de ondas EM, que lhes dá versatilidade ao transformar sua energia, que é proporcional à frequência.

A Figura 2 mostra uma onda eletromagnética, nela o campo elétrico E Em azul, oscilados no avião ZY, O campo magnético B Em vermelho, isso faz isso no avião XY, Enquanto a velocidade da onda é direcionada ao longo do eixo +e, De acordo com o sistema de coordenadas mostrado.

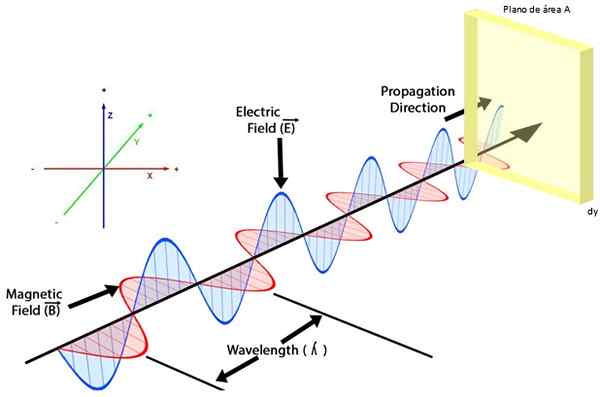Figura 2. Uma onda eletromagnética que afeta uma superfície fornece energia de acordo com o vetor de poynting. Fonte: f. Zapata.

Se no caminho de ambas as ondas, uma superfície for trazida, digamos um plano de área PARA e espessura Dy, De modo que é perpendicular à taxa de onda, o fluxo de energia eletromagnética por unidade de área, denotada S, é descrito através Vetor de poynting:

S = (1 /μ_qualquer) E × B

μ_qualquer É a permeabilidade do vácuo (μ_qualquer = 4π .10^-7 Tesla. Metrô/ampere), Uma constante relacionada à facilidade que o meio dá à onda eletromagnética para se mover.

Pode atendê -lo: anão branco

O vetor de Poynting foi introduzido pelo astrofísico inglês John Henry Poynting em 1884, pioneiro no estudo energético de campos elétricos e magnéticos.

Poder instantâneo por unidade de área

Agora, devemos levar em consideração que a energia é um escalar, enquanto S É um vetor.

Lembrando que o poder é a energia fornecida por unidade de tempo, então o módulo de S Indica o Poder instantâneo por unidade de área Na direção da propagação da onda eletromagnética (taxa de transferência de energia).

Sendo que E e B Eles são perpendiculares um ao outro, o módulo de E x B É simplesmente eb E o poder instantâneo (um escalar) permanece:

S = (1 /μ_qualquer) Eb

É fácil verificar se as unidades são watt/m² No sistema internacional.

Ainda há mais. As magnitudes dos campos E e B Eles estão relacionados entre si através da velocidade da luz c. De fato, ondas eletromagnéticas no vácuo se espalham assim. Este relacionamento é:

E = cb

Substituindo esse relacionamento em S é obtido:

S = (1 /μ_qualquer.EC²

O vetor de poynting varia com o tempo de sinusoidal, portanto a expressão anterior é seu valor máximo, porque a energia fornecida pela onda eletromagnética também oscila, assim como os campos fazem. Obviamente, a frequência de oscilação é muito grande, por isso não é possível detectá -la sob luz visível, por exemplo.

Formulários

Entre os múltiplos usos que já disseram ter energia eletromagnética, aqui estão dois que são usados ​​continuamente em inúmeras aplicações:

Antena DiPolo

As antenas estão por toda parte preenchendo o espaço com ondas eletromagnéticas. Existem transmissores, que transformam sinais elétricos em ondas de rádio ou microondas, por exemplo. E existem receptores que fazem o trabalho reverso: eles coletam as ondas e os tornam sinais elétricos.

Vamos ver como criar um sinal eletromagnético que se espalha no espaço, de um dipolo elétrico. O dipolo consiste em duas cargas elétricas de igual magnitude e sinais opostos, separados por uma pequena distância.

Pode atendê -lo: condutores elétricos

Na figura seguinte está o campo elétrico E Quando o carregamento + está acima (figura esquerda). E pontos para baixo no ponto mostrado.

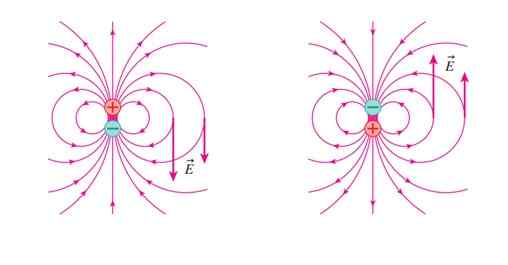Figura 3. Campo elétrico de um dipolo em duas posições diferentes. Fonte: Randall Knight. Física para cientistas e engenheiros.

Na Figura 3 à direita, o dipolo mudou de posição e agora E aponta. Repetimos essa mudança muitas vezes e muito rápido, digamos a frequência F. Um campo é criado então E A variável no tempo dá origem a um campo magnético B, também variável e cuja forma é seno (veja a Figura 4 e abaixo do exemplo 1).

E como a lei de Faraday garante que um campo magnético B A variável no tempo dá origem a um campo elétrico, porque acontece que fazer o dipolo já possui um campo eletromagnético capaz de espalhar.

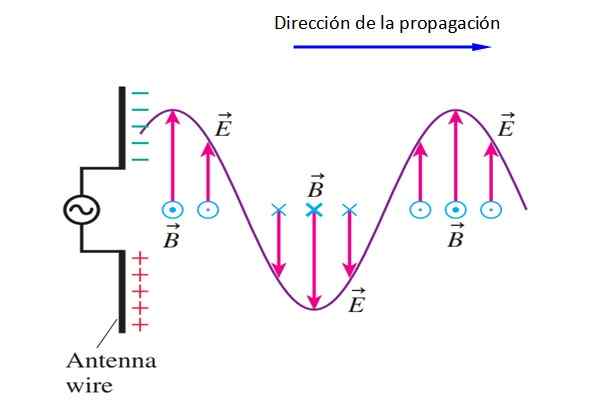Figura 4. Uma antena dipolo gera um sinal que transporta energia eletromagnética. Fonte: f. Zapata.

Eu sinto isso B pontos dentro ou fora da tela alternadamente (é sempre perpendicular a E).

Energia de campo elétrico: o condensador

Os capacitores têm a virtude de armazenar carga elétrica e, portanto, energia elétrica. Eles fazem parte de numerosos dispositivos: motores, circuitos de rádio e televisão, sistema de luz de carro e muito mais.

Os capacitores consistem em dois motoristas separados, uma pequena distância. Cada um é conferido uma carga de igual magnitude e o sinal oposto, depois criando um campo elétrico no espaço entre os dois drivers. A geometria pode variar, sendo bem conhecida do capacitor de placa paralelo paralelo.

A energia armazenada em um condensador vem do trabalho que foi feito para carregá -lo, que serviu para criar o campo elétrico dentro. Apresentando um material dielétrico entre as placas, a capacidade do capacitor aumenta e, portanto, a energia que isso pode armazenar.

Um capacitor de capacidade e descarregado inicialmente, que é carregado por uma bateria que fornece uma tensão V, até atingir uma carga q, armazena uma energia ou dada por:

U = ½ (q²/C) = ½ qv = ½ cv²

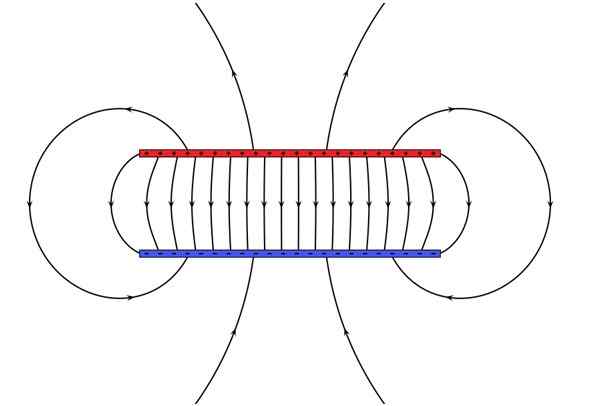Figura 5. Uma placa plana paralela armazena a energia eletromagnética. Fonte: Wikimedia Commons. Geek3 [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenças/BY-SA/4.0)].

Exemplos

Exemplo 1: Intensidade de uma onda eletromagnética

Anteriormente, foi dito que a magnitude do vetor de poynting é equivalente ao poder que a onda oferece para cada metro quadrado de superfície e que, além disso, sendo o vetor dependente do tempo, seu valor oscilou até um máximo de um máximo de S = s = (1 /μ_qualquer.EC².

O valor médio de S em um ciclo de onda é fácil de medir e indicativo da energia da onda. Este valor é conhecido como intensidade da onda E é calculado dessa maneira:

Pode atendê -lo: o que é equilíbrio dinâmico? (Com exemplo)

I = s_metade = S = (1 /μ_qualquer.EC²_metade

Uma onda eletromagnética é representada por uma função seno

E = e_qualquer Sen (KX - ωt)

Onde E_qualquer É a amplitude da onda, k O número da onda e Ω A frequência angular. Então:

O valor médio da função sen² x em um ciclo é ½. É formalmente calculado pela seguinte expressão, o que é possível verificar com a ajuda de uma tabela integral ou executar a integral analiticamente:

Portanto s_metade Permanece como:Quando uma fonte emite igualmente em todas as direções, o poder é irradiado de acordo com o inverso para o quadrado da distância à fonte (Figura 5). Sim P_m É a potência média, então, à distância r A intensidade Yo do sinal, é dado por:

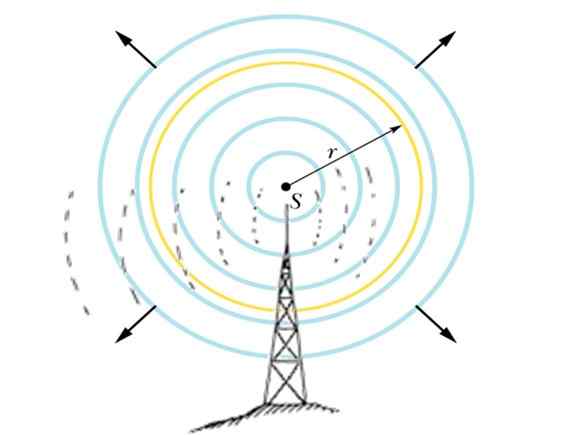Figura 5. A antena irradia o sinal em forma esférica. Fonte: f. Zapata.

Exemplo 2: Aplicação a uma antena de transmissão

Há uma estação de rádio que transmite um sinal de 10 kW de potência e frequência de 100 MHz, que se espalha de forma esférica, como na figura acima.

Encontre: a) A amplitude dos campos elétricos e magnéticos em um ponto localizado a 1 km da antena e b) a energia eletromagnética total que afeta uma folha quadrada 10 cm em um período de 5 minutos.

Os dados são:

Velocidade da luz no vácuo: C = 300.000 km/s

Permeabilidade a vácuo: μ_qualquer = 4π .10^-7 T.M/A (Tesla. Metrô/ampere)

Solução para

A equação dada no Exemplo 1 é usada para encontrar a intensidade da onda eletromagnética, mas primeiro os valores no sistema internacional devem ser expressos:

10 kW = 10000 W

100 MHz = 100 x 10⁶ Hz

IR Esses valores são substituídos na equação para intensidade, pois é uma fonte que emite igualmente (fonte isotrópico):

Esta é precisamente a potência média por unidade de área média ou valor do módulo vetorial de Poynting:

Anteriormente foi dito que as magnitudes de E e B Eles foram relacionados pela velocidade da luz:

E = cb

B = (0.775/300.000.000) t = 2.58 x 10^-9 T

Solução b

S_metade É energia por unidade de área e, por sua vez, a energia é energia por unidade de tempo. Multiplicando s_metade Para a área da placa e para o tempo de exposição, o resultado solicitado é obtido:

5 minutos = 300 segundos

Área = (10/100)²  m² = 0.01 m².

U = 0.775 x 300 x 0.01 Joules = 2.325 Joules.

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 6. Eletromagnetismo. Editado por Douglas Figueroa (USB). 307-314.
2. ICES (Comitê Internacional de Segurança Eletromagnética). Fatos eletromagnéticos de energia e uma visão qualitativa. Recuperado de: iCes-emfsafety.org.
3. Cavaleiro, r. 2017. Física para cientistas e engenharia: uma abordagem de estratégia. Pearson. 893 - 896.
4. Universidade Estadual de Portland. EM Waves Trate Energy. Recuperado de: pdx.Edu
5. O que é energia eletromagnética e por que é importante?. Recuperado de: sciencestruck.com.