Elipse

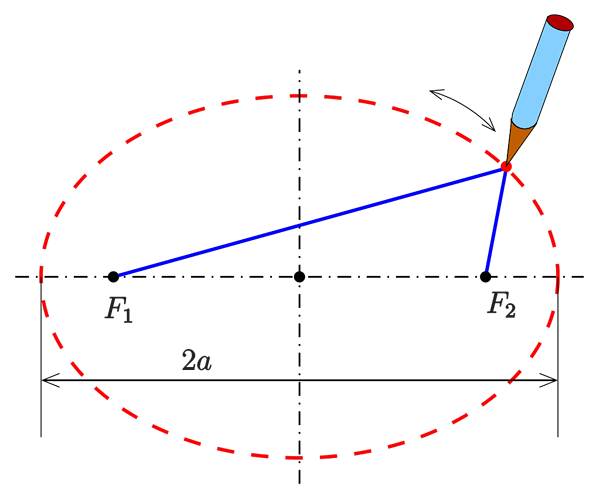
figura 1. Método do jardineiro para desenhar uma elipse. A soma das distâncias entre um ponto P da elipse (em vermelho) e os holofotes (em preto) permanece constante. Fonte: Ag2gaeh, CC BY-SA 4.0, via Wikimedia Commons.

O que é uma elipse?

Uma elipse é um conjunto de pontos de coordenadas (x, y), para os quais a soma das distâncias para dois pontos fixos, chamados Focos, é constante. Por sua vez, os holofotes são separados um do outro uma distância igual a 2C.

As elipses são encontradas na natureza. Por exemplo, está no movimento da Terra ao redor do sol, pois como demonstrado pela astronom alemã.

Além disso, a forma elíptica é encontrada no projeto de construções arquitetônicas, faz parte de um tratamento médico para destruir os cálculos renais e serve para moldar diversos objetos, como tanques e outros contêineres.

Na figura superior, uma elipse é mostrada com seus dois holofotes, localizados equidistantes do centro da figura e no eixo mais longo. A condição de que um ponto P deve se encontrar para pertencer à elipse é que a soma das distâncias a cada foco é fixa:

d₁ + d₂ = constante.

Portanto, quando um jardineiro quer. Em seguida, pegue uma corda de bom tamanho, amarre suas pontas nas apostas e apoiando um bastão na corda desliza nela para marcar o sulco elíptico na terra macia. Este é ele Método do jardineiro Para desenhar elipses.

ELEMENTOS DE ELIPSE

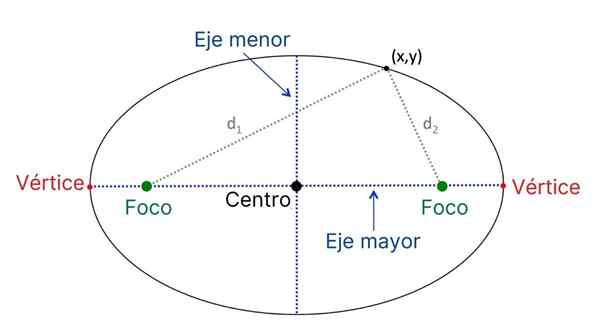Principais elementos de uma elipse

Estes são os principais elementos da elipse:

1. Focos, Pontos fixos localizados no eixo mais longo da elipse.
2. Vértices, Eles são os dois pontos da elipse através dos quais a linha passa que se une aos holofotes.
3. Eixo principal, É a corda que se junta aos vértices e também contém os holofotes.
4. Centro, Ponto médio do eixo principal, que corresponde ao ponto de coordenada (h, k). Cada foco é equidistante do centro e à distância c do mesmo.
5. Eixo menor, É a corda que passa pelo centro e é perpendicular ao eixo principal.
6. Rádios vetoriais, segmentos que unem cada foco com um P da elipse.
7. Eixo focal, diretamente em que os holofotes são.
8. Distância focal, É a distância entre os holofotes, indicada como 2C.
9. Eixo secundário, eixo perpendicular ao eixo principal, que é ao mesmo tempo media tutrix do segmento que se liga aos holofotes.
10. Centro de Simetria, ponto coincidindo com o centro da elipse, onde os eixos de simetria do mesmo são cruzados.
11. Eixos de simetria, linhas que contêm os maiores e menores eixos da elipse.

Pode atendê -lo: Tributação

Tipos de elipse

Existem dois tipos de elipse:

• Aqueles que têm o eixo principal horizontal.
• Aqueles que têm o maior eixo vertical.

Então eles são descritos matematicamente:

Ellipse com o principal eixo horizontal

Deixe o ponto C das coordenadas (H, k) o centro da elipse, o comprimento do eixo principal é 2a e o comprimento do eixo menor igual a 2b, com A> B.

A equação desta elipse é:

Ellipse com o principal eixo vertical

Com os mesmos parâmetros da elipse com um eixo horizontal, a elipse com o principal eixo vertical é escrita como:

Nos dois casos, a distância do foco ao centro c Está relacionado aos sedimentos maiores e menores através de:

c² = a² - b²

Exemplos de elipses

Ellipse horizontal

A imagem a seguir mostra uma elipse cujo principal eixo é horizontal. O centro está no ponto (0,0) e os holofotes em (-3,0) e (3.0) respectivamente. Ponto P (0, -4) destacado pertence à elipse.

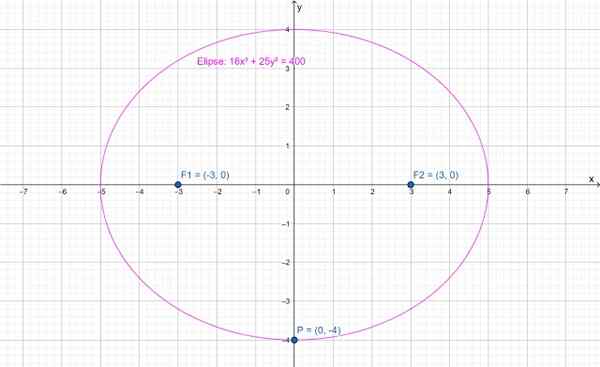Figura 2.- Elipse cujo principal eixo é horizontal. Fonte: f. Zapata através da Geogebra.

A equação desta elipse é:

16x² + 25 e² = 400

Não é difícil expressar essa equação na forma canônica, é suficiente dividir todos os termos entre 400 e simplificar convenientemente (veja o exercício resolvido posteriormente).

Elipse vertical

A seguir, é apresentado uma elipse vertical, cujo principal eixo coincide com o eixo e. Está focado no ponto (0,0) e sua equação é:

36x² + 9y² = 324

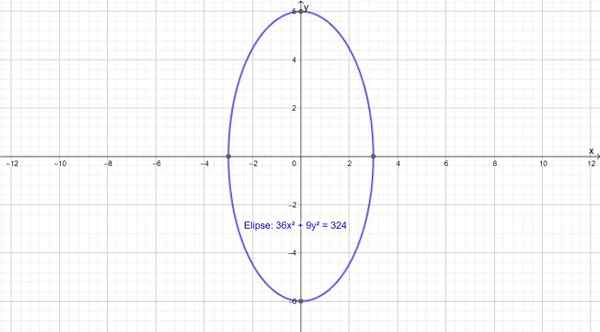Figura 3.- Uma elipse com o principal eixo vertical. Fonte: f. Zapata através da Geogebra.

Propriedade de reflexão

Consiste no seguinte: Se um refletor ou uma fonte de som for colocado em um dos holofotes Ellipse, as ondas emitidas são refletidas para o outro foco. É uma boa maneira de redirecionar as ondas onde sua energia é necessária.

Pode atendê -lo: Endecagon

É por isso que nos salões elípticos, quando uma pessoa fala estar em um dos holofotes, um ouvinte localizado no outro foco escuta claramente.

E, na medicina. As ondas são refletidas nos cálculos e os fragmentam em partículas menores, que são então expulsas pela urina.

O Rádio Ska

Este radiotelescópio é o maior do tipo e deve começar a trabalhar em 2021. Sua superfície é de 1 km quadrada e é por isso que é chamado de ska (em inglês eles são o acrônimo para Matriz de quilômetros quadrados).

Aproveitando a propriedade de reflexão das elipses, a estrutura consiste em um arranjo de 3000 antenas com forma elíptica de cerca de 15 m de largura, distribuída entre a Austrália e a África do Sul. Com este instrumento, 50 vezes mais sensível do que aqueles em uso agora, espera -se que ele dê uma olhada no universo quando ainda era muito mais jovem: cerca de um bilhão de anos mal.

Figura 4.- Interpretação artística do Ska Radio Ska. Fonte: Wikimedia Commons.

Exercício resolvido

Encontre as equações canônicas das elipses mostradas nas Figuras 2 e 3 e em cada caso determine os comprimentos dos sentidos maiores e menores, bem como distâncias focais.

Solução

Para a elipse horizontal, cuja equação é 16x² + 25 e² = 400, todos os termos entre 400 são divididos, resultantes:

Pode servir a você: derivado de cotangent: cálculo, demonstração, exercícios

 Que é simplificado:

O eixo “A” mede 5 e o menor “B” mede 4, que também é avisado ao observar a imagem cuidadosamente. Quanto à distância focal, você precisa:

c² = a² - b²

c² = 25 - 16 = 9 ⇒ c = √9 = 3

Portanto, C = 3 é a distância entre o centro e um dos holofotes. Ambos os focos são uma distância 2C = 6.

Quanto ao elipse vertical 36x² + 9y² = 324 você tem:

Simplificando:

c² = 36 - 9 = 27

C = √27 ≅ 5.2

Portanto, a distância entre os holofotes é 10.4 unidades.

Referências

1. Hoffman, J. Seleção de questões de matemática. Volume 3.
2. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
3. Fórmulas do Universo. A elipse. Recuperado de: universoformulas.com.
4. Wikipedia. Matriz de quilômetros quadrados. Recuperado de: é.Wikipedia.org.
5. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.