Descrição do efeito Doppler, fórmulas, casos, exemplos

Ele efeito Doppler É um fenômeno físico que ocorre quando o receptor e a fonte das ondas têm movimento relativo, causando uma mudança na frequência do receptor em relação à frequência da fonte.

Seu nome é devido ao físico austríaco Christian Doppler (1803-1853), que descreveu e explicou esse fenômeno em 1842, enquanto apresentava um trabalho sobre a cor das estrelas duplas, em um congresso de ciências naturais em Praga, a atual república tcheca.

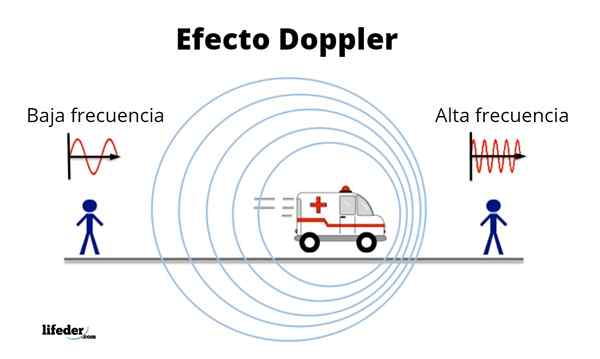
Ilustração do efeito Doppler

[TOC]

Onde o efeito Doppler é apresentado?

A figura ilustra uma fonte de ondas que se move da esquerda para a direita. Um observador à frente da fonte percebe comprimentos de onda curtos e o oposto para um observador atrás. Fonte: Wikimedia Commons.

O efeito Doppler é apresentado em todos os tipos de ondas, do luminoso ao som, desde que a fonte e o receptor estejam se movendo um sobre o outro. E é muito mais notável quando a velocidade relativa entre a fonte e o receptor é comparável à velocidade de propagação da onda.

Suponha que uma onda harmônica, que é uma oscilação que avança no espaço. A oscilação é repetida em intervalos de tempo regular, desta vez é o período e seu inverso freqüência, esse é o número de oscilações por unidade de tempo. 

Quando a distância entre a fonte da onda harmônica e o receptor permanece fixa, o receptor percebe a mesma frequência de fonte, ou seja, registra o mesmo número de pulsos por unidade de tempo que a fonte. 

No entanto, quando o receptor se aproxima da fonte com velocidade fixa, os pulsos estão chegando com mais frequência. E o oposto ocorre quando o receptor se afasta da velocidade fixa da fonte: os pulsos das ondas são percebidos com uma frequência mais baixa.

Descrição do efeito Doppler

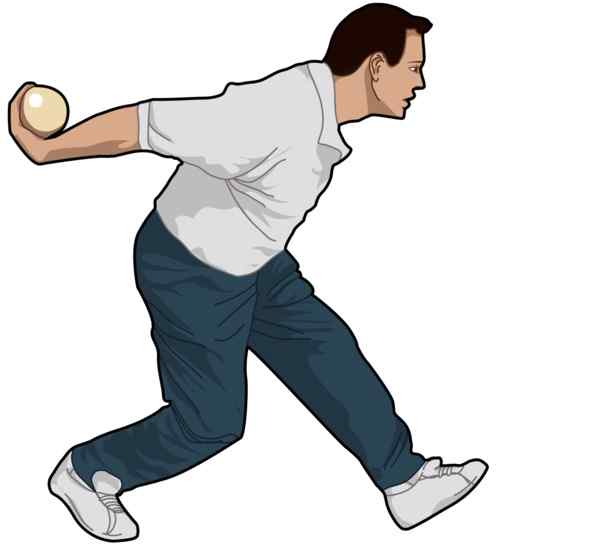
Para entender por que esse fenômeno ocorre, usaremos uma analogia: duas pessoas jogando bolas. O arremessador os faz rolar em uma linha reta no chão em direção ao parceiro, o que os pega.

Se a pessoa que lançar enviar uma bola a cada segundo, quem a coleta, se permanecer fixa, pegará uma bola a cada segundo. Tudo de bom até agora, já que é esperado.

O recepor de movimento

Agora, suponha que a pessoa que pega as bolas esteja em um skate e decida se aproximar do jarro com velocidade constante. Nesse caso, quando você vai encontrar as bolas, você terá menos de um segundo entre uma bola e o seguinte.

Portanto, o receptor parece ser mais de uma bola por segundo, ou seja, a frequência com que eles alcançam sua mão aumentada. 

Pode servir a você: Física durante os gregos (Antige Grécia)

O oposto aconteceria se a pessoa receptora decidisse se afastar do emissor, ou seja, o tempo de chegada das bolas aumentaria com a conseqüente diminuição da frequência com que as bolas chegam.

Fórmulas

A alteração da frequência descrita na seção anterior pode ser obtida na seguinte fórmula:

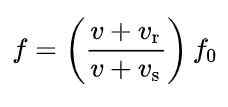
Aqui:

-F_qualquer É a frequência da fonte.
-F é a frequência aparente no receptor.
-v é a velocidade (v> 0) da propagação da onda no meio.
-v_r é a velocidade do receptor em relação ao meio ambiente e
-v_s é a velocidade da fonte relacionada ao meio.

Observe que v_r É positivo se o receptor se aproximar da fonte e negativo. Por outro lado, v_s É positivo se a fonte se afastar do receptor e negativa quando se aproxima.

Em resumo, se a fonte e a abordagem do observador, a frequência aumentar e se eles se afastarem diminuirem. O oposto ocorre com o aparente comprimento de onda no receptor (ver Exercício 1).

Casos em que o efeito doppler existe

Velocidade da fonte e receptor muito mais baixo que a onda

Freqüentemente acontece que a velocidade da onda é muito maior que a velocidade com que a fonte ou a velocidade do movimento do receptor se move.

Nesse caso, a fórmula pode ser aproximada de forma a ser escrita com base na velocidade relativa do receptor (observador) em relação à (s) fonte (s).

Nesse caso, a fórmula seria assim:

F = [1 + (VRS/V)] ⋅f_qualquer

Onde V_Rs = v_r - v_s.

Quando v_Rs É positivo (eles se aproximam), a frequência f é maior que f_qualquer, enquanto quando é negativo (eles se afastam), f é menor que f_qualquer.

Ângulo de formação de velocidade relativa com a posição relativa

A fórmula anterior se aplica apenas ao caso que a fonte se aproxima (ou se afasta) diretamente do observador.

No caso de a fonte se mover após um caminho transversal, é necessário.

Nesse caso, devemos nos inscrever:

F = [1 + (V_Rs ⋅ cos (θ) / v)] ⋅ f_qualquer

Novamente, um v_Rs Sinal positivo é atribuído se o receptor e a fonte estiverem se aproximando e negativos se ocorrer pelo contrário.

Exemplos de efeito Doppler

Um exemplo diário é a sirene de uma ambulância ou patrulha. Quando se aproximar de nós é mais agudo e, quando se move, é mais sério, principalmente a diferença é ouvida no momento da abordagem máxima.

Pode servir a você: trajetória física: características, tipos, exemplos e exercícios

Outra situação que é explicada pelo efeito Doppler é a mudança das linhas espectrais das estrelas em direção a azul ou vermelho, se elas estiverem se aproximando de nós ou se estiverem se afastando. Isso não pode ser notado a olho nu, mas com um instrumento chamado espectrômetro.

Formulários

O efeito Doppler tem muitas aplicações práticas, alguns estão listados abaixo:

Radares

Os radares medem a distância e a velocidade em que os objetos detectados por ele se movem e são baseados com precisão no efeito doppler.

O radar emite uma onda em direção ao objeto que você deseja detectar, então essa onda é refletida de volta. O tempo que leva para um pulso ir e voltar para determinar a distância à qual o objeto é. E a mudança de frequência no sinal refletido permite saber se o objeto em questão se afasta ou se aproxima quando o radar e a rapidez.

Como a onda de radar vai e retorna, há um efeito de doppler duplo. Nesse caso, a fórmula que permite determinar a velocidade do objeto em relação ao radar é:

V_ou = ½ C ⋅ (ΔF / F_qualquer)

Onde:
-V_ou É a velocidade do objeto em relação ao radar.
-c a velocidade da onda emitida e depois refletiu.
-F_qualquer A frequência de emissão de radar.
-Δf a mudança de frequência, ou seja, f - f_qualquer.

Astronomia

Graças ao efeito Doppler, foi determinado que o universo está se expandindo, uma vez que o espectro da luz emitido por galáxias distantes é deslocado para o vermelho (uma diminuição da frequência).

Por outro lado, também se sabe que a velocidade da partida cresce na medida em que as galáxias observadas estão mais distantes.

Caso contrário, ocorre com algumas galáxias do grupo local, ou seja, os vizinhos da nossa Via Láctea.

Por exemplo, nosso vizinho mais próximo, a galáxia de Andrômeda tem uma ascensão azul (ou seja, um aumento na frequência) indicando que estamos nos aproximando de nós.

Ultrassom Doppler

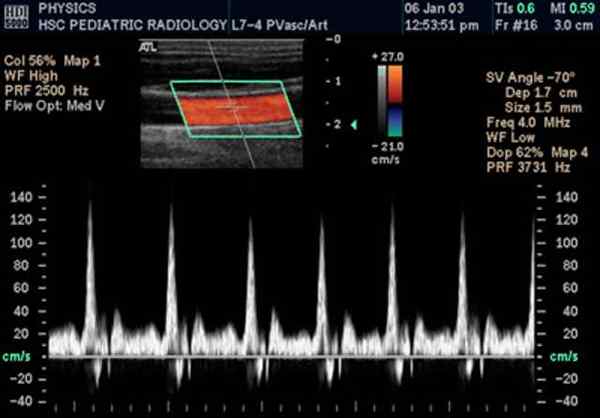Ultrassom doppler da artéria carótida. Fonte: Wikimedia Commons.

É uma variante do ecossonograma tradicional, no qual aproveitar o efeito doppler a velocidade do fluxo sanguíneo em veias e artérias é medido.

Exercícios

Exercício 1 

A sirene de uma ambulância tem uma frequência é de 300 Hz. Sabendo que a velocidade do som no ar é de 340 m/s, determine o comprimento de onda do som nos seguintes casos:

Pode servir a você: Curva de calibração: para que é, como fazer isso, exemplos

a) Quando a ambulância está em repouso.

b) Se você se aproximar de 108 km/h 

c) Ao se afastar na mesma velocidade.

Solução para

Não há efeito Doppler porque o emissor e a fonte estão em repouso.

Para determinar o comprimento de onda do som, a relação entre a frequência do final F, o comprimento de onda λ da fonte e a velocidade do som V:

v = f_qualquer⋅λ.

A partir daí, segue -se:

λ = v / f_qualquer.

Portanto, o comprimento de onda é:

λ = (340 m/s)/(300 1/s) = 1,13 m.

Solução b

O receptor é considerado em repouso, ou seja, que_r = 0. O emissor é a sirene que se move com a rapidez da ambulância:

v_s = (108/3,6) m/s = 30 m/s.

A aparente frequência f é dada pelo relacionamento:

f = f_qualquer⋅ [(V + V_r)/(V + V_s)]

A aplicação desta fórmula é obtida:

F = 300 Hz ⋅ [(340 + 0)/(340 - 30)] = 329 Hz.

O comprimento de onda no receptor será:

λ_r= v / f = (340 m / s) / (329 1 / s) = 1,03 m.

Solução c

É resolvido da mesma forma:

F = 300 Hz ⋅ (340 + 0)/(340 + 30) = 276 Hz.

O comprimento de onda no receptor será:

λ_r = v / f = (340 m / s) / (276 1 / s) = 1,23 m.

Conclui -se que as frentes de onda têm uma separação de 1,03 m quando a sirene está se aproximando e 1,23 m quando se afasta.

Exercício 2

Uma linha característica do espectro de emissão de hidrogênio é de 656 nm, mas ao observar uma galáxia, é visto que a mesma linha é deslocada e marcas de 660 nm, ou seja, possui uma mudança vermelha de 4 nm.

Como há um aumento no comprimento de onda, sabemos que a galáxia se afasta. Qual é a sua velocidade? 

Solução

O quociente entre o deslocamento do comprimento de onda e o comprimento de onda de repouso é igual ao quociente entre a velocidade da galáxia e a velocidade da luz (300.000 km/s). Então:

4/656 = 0.006

Portanto, a galáxia se afasta em 0.006 vezes a velocidade da luz, ou seja, 1800 km/s.

Referências

1. Alonso - Finn. Vol Physics.2. 1970. Fundo Educacional Inter -Americano, S.PARA. 
2. Baranek, l. 1969. Acústica. 2º. Edição. McGraw Hill.
3. Griffiths g. Ondas lineares e não lineares. Recuperado de: Scholarpedia.org.
4. Whitham g.B. 1999. Ondas lineares e não lineares. Wiley. 
5. Wikiwaves. Ondas não lineares. Recuperado de: wikiwaves.org
6. Wikipedia. efeito Doppler. Recuperado de: é.Wikipedia.com