Fórmula de equações de segundo grau, como resolvê -las, exemplos, exercícios
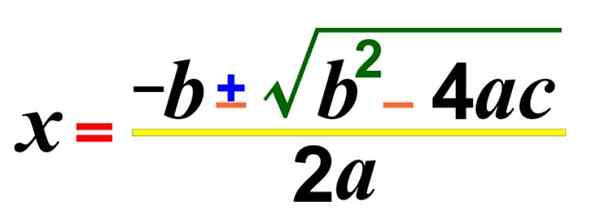
- 4961
- 953
- Terrell Stokes
As Segundo grau ou equações quadráticas E um desconhecido tem o formulário machado2 + BX + C = 0. Onde a ≠ 0, como sendo 0, a equação seria transformada em uma equação linear, e os coeficientes a, b e c são números reais.
O desconhecido a ser determinado é o valor de x. Por exemplo, a equação 3x2 - 5x + 2 = 0 é uma equação completa do segundo grau.
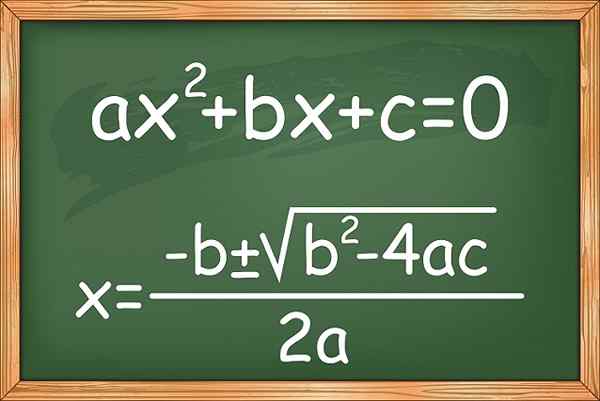 figura 1. A fórmula para resolver equações de segundo grau ou quadrático de um desconhecido
figura 1. A fórmula para resolver equações de segundo grau ou quadrático de um desconhecido Também existem variantes conhecidas como equações incompletas de segundo grau, que não possuem qualquer um dos termos, exceto o de machado2. aqui estão alguns exemplos:
x2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, o famoso matemático árabe da antiguidade, descrito em seus trabalhos vários tipos de equações de primeiro e segundo grau, mas apenas com coeficientes positivos. No entanto, era o matemático francês Resolvente:
Esta é uma fórmula geral que permite resolver uma equação quadrática, encontrando as raízes ou zeros do mesmo, mesmo que as soluções não sejam reais. Também existem outras maneiras de resolvê -los.
[TOC]
Como resolver equações da segunda série?
As equações de segundo grau podem ser resolvidas pela fórmula dada acima, e também existem outros procedimentos algébricos que podem funcionar em algumas equações.
Vamos resolver a equação proposta no começo com a fórmula, um método válido para qualquer equação de segundo grau com um desconhecido:
3x2 - 5x + 2 = 0
Para usar a fórmula, observamos corretamente que:
- para É o coeficiente do termo com x2
- b É o coeficiente do termo linear
- c é o termo independente.
Vamos identificá -los da mesma equação:
A = 3
B = -5
C = 2
Observe que o sinal de que acompanha o coeficiente deve ser levado em consideração. Agora substituímos esses valores na fórmula:
No numerador está o símbolo de "mais - menos" ±, o que indica que a quantidade com raiz pode ser tomada como positiva e também como negativa. Uma equação de segundo grau tem no máximo duas soluções reais, e este símbolo leva em consideração.
Vamos ligar para x1 e x2 Para essas duas soluções, então:
x1 = (5+1) / 6 = 1
x2 = (5-1)/6 = 4/6 = 2/3
Resolução por fatoração
Algumas equações de segundo grau consistem em trinômios que são facilmente fatorados. Nesse caso, esse método é muito mais rápido. Considere a equação:
x2 + 7x - 18 = 0
A fatorização tem esse formulário:
Pode servir a você: congruência: figuras congruentes, critérios, exemplos, exercícios(x +) ⋅ (x -)
Os espaços em branco são preenchidos com dois números que, quando multiplicados em 18, e quando são subtraídos, 7 são 7. Os sinais entre parênteses são escolhidos com este critério:
-No primeiro parêntese, o sinal entre o primeiro e o segundo termo é colocado.
-E no segundo parêntese, segue o produto dos sinais que são vistos.
Quanto aos números, eles são facilmente neste caso: eles são 9 e 2. O mais velho é sempre colocado no primeiro dos parênteses, assim:
x2 + 7x - 18 = (x + 9). (x - 2)
O leitor pode verificar através da propriedade distributiva, que ao desenvolver o produto do lado direito da igualdade, o trinômio da esquerda é obtido. Agora, a equação é reescrita:
(x + 9) ⋅ (x - 2) = 0
Para que a igualdade seja cumprida, é suficiente para que um dos dois fatores seja zero. Então, no primeiro, tem que ser feito1 = -9 ou pode ser que o segundo fator seja cancelado, nesse caso x2 = 2. Estas são as soluções de equação.
Método gráfico
As raízes ou soluções da equação de segundo grau correspondem às interseções da parábola y = = = machado2 + BX + c Com o eixo horizontal ou o eixo x. Para que, gráficando a parábola correspondente, encontraremos a solução da equação de segundo grau fazendo y = 0.
Os cortes das parábolas com o eixo horizontal representam as soluções da equação machado2 + BX + C = 0. Uma parábola que só corta o eixo horizontal em um único ponto tem uma única raiz e este sempre será o vértice da parábola.
E finalmente, se uma parábola não cortar no eixo horizontal, a equação correspondente machado2 + BX + C = 0 Falta soluções reais.
Construir um gráfico de mão pode ser trabalhoso, mas com o uso de programas que gráficos online é muito simples.
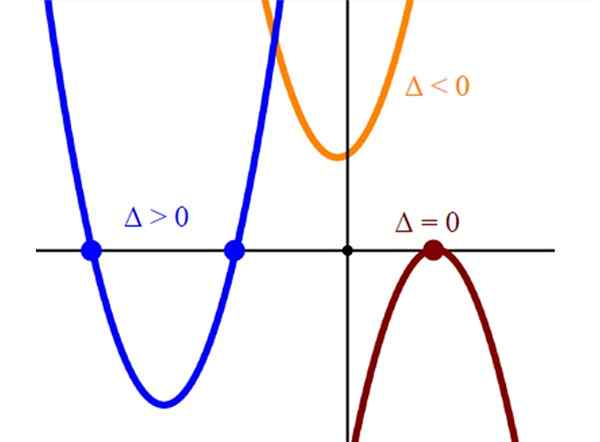 Figura 2. Representação gráfica de três tipos de parábolas, com dois, um e sem interseção com o eixo horizontal. Fonte: Wikimedia Commons.
Figura 2. Representação gráfica de três tipos de parábolas, com dois, um e sem interseção com o eixo horizontal. Fonte: Wikimedia Commons. Resolução com calculadora científica
Muitos modelos de calculadoras científicas têm a opção de resolver equações de segundo grau (e também outros tipos de equações). Para saber, você tem que revisar o menu.
Uma vez que a opção de equação quadrática de um desconhecida é escolhida, o menu solicita para inserir os valores dos coeficientes A, B e C e retornar as soluções reais se existirem. E também existem modelos de calculadoras científicas que trabalham com números complexos e oferecem essas soluções.
Pode atendê -lo: múltiplos de 2: o que são e explicaçãoDiscriminar de uma equação de segundo grau
Para saber se a equação tem soluções reais ou não, e quantos são, sem a necessidade de resolver primeiro, o discriminante é definido como a quantidade sob a raiz quadrada:
Δ = b2 - 4ac
De acordo com o sinal discriminante, sabe -se quantas soluções a equação tem de acordo com este critério:
-Duas soluções reais: Δ> 0
-Uma solução real (ou duas soluções idênticas): δ = 0
-Nenhuma solução real: δ < 0
Por exemplo, quantas soluções a equação de segundo grau tem -7x2 +12x + 64 = 0? Identificamos os coeficientes:
A = -7
B = 12
C = 64
Δ = b2 - 4ac = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
A equação tem duas soluções. Agora vamos ver este:
x2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Esta é uma equação com uma solução única ou duas soluções iguais.
Exemplos de equações simples de segundo grau
No começo, dissemos que as equações de segundo grau poderiam ser completas se o trinomial estiver, e incompleto se o termo linear ou o termo independente estivesse ausente. Agora vamos ver alguns tipos específicos:
X equação de forma2 + mx + n = 0
Nesse caso A = 1 e a fórmula é reduzida a:
Para esse tipo de equação e sempre dependendo dos coeficientes restantes, o método de fatorização pode funcionar bem, como vimos na seção anterior.
Equação incompleta do formulário de machado2 + C = 0
A solução, se existe, é o formulário:
Há uma solução real quando um o c tem um sinal negativo, mas se os dois termos tiverem o mesmo sinal, a solução será imaginária.
Equação incompleta do formulário de machado2 + Bx = 0
Esta equação é rapidamente resolvida usando a fatorização, pois o X é um fator comum em ambos os termos. Uma das soluções é sempre x = 0, a outra é assim:
machado2 + Bx = 0
x (ax + b) = 0
ax + b = 0 → x = -b/a
Vejamos um exemplo então. Resolver:
x2 - 5x = 0
x (x - 5) = 0
Portanto x1 = 0 e x2 = 5
Equações com denominador
Existem várias equações racionais, nas quais o desconhecido pode estar presente tanto no numerador quanto no denominador, ou mesmo apenas neste último, e que por manipulações algébricas são reduzidas a equações quadráticas.
A maneira de resolvê -los é multiplicar os dois lados da igualdade pelo mínimo múltiplo comum ou m.c.m dos denominadores e depois reorganize os termos. Por exemplo:
Pode atendê -lo: quantos diâmetros uma circunferência tem?Equações de ordem superior que são transformadas em quadrático
Existem equações de ordem superior que, através de uma mudança variável, podem ser resolvidas como se fossem quadráticas, por exemplo, esta equação Bicadrada:
x4 - 10x2 + 9 = 0
Deixe x2 = U, então a equação é transformada em:
ou2 - 10U + 9 = 0
Esta equação é rapidamente resolvida pela fatoração, encontrando dois números que se multiplicaram em 9 e adicionados 10. Esses números são 9 e 1:
(U - 9).(U - 1) = 0
Portanto, as soluções desta equação são você1 = 9 e você2 = 1. Agora retornamos a mudança:
x2 = 9 → X1 = 3 e x2 = -3
x2 = 1 → X1 = 1 e x2 = -1
A equação original é da Ordem 4, portanto tem pelo menos 4 raízes. O exemplo é -3, -1, 1 e 3.
Exercícios simples resolvidos
- Exercício 1
Resolva a seguinte equação quadrática com o desconhecido no denominador:
O múltiplo comum mínimo é x (x+2) e deve se multiplicar a todos os termos:
A expressão equivalente permanece:
5x (x+2) - x = x (x+2)
Nós desenvolvemos:
5x2 + 10x - x = x2 + 2x
Todos os termos são transpostos à esquerda da igualdade e à direita fica 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
Factamos, pois é uma equação incompleta:
x (4x - 7) = 0
Uma das soluções é x = 0, a outra é:
4x = 7
x = 7/4
- Exercício 2
Encontre a solução das equações de segundo grau:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Solução para
A partir desta equação, conhecemos o determinante Δ, porque foi calculado como um exemplo antes, por isso vamos aproveitar isso, expressando a fórmula do solvente da seguinte maneira:
x1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
x2 = (-12 -44) / -14 = 4
Solução b
O quadrado trinomial x2 - 6x + 9 é fatorável, pois é um trinômio quadrado perfeito:
x2 - 6x + 9 = (X-3)2 = 0
A solução desta equação é x = 3.
- Exercício 3
Qual é a equação cujas soluções são 3 e 4?
Solução
A expressão fatorizada é:
(x - 3) ⋅ (x - 4) = 0
Aplicando propriedade distributiva:
x2 - 4x -3x + 12 = 0
Os dois termos centrais são semelhantes e podem ser reduzidos, sendo: saindo:
x2 - 7x + 12 = 0
Referências
- Baldor. 1977. Álgebra Elementar. Edições culturais venezuelanas.
- Hoffman, J. Seleção de questões de matemática. Volume 2.
- Jiménez, r. 2008. Álgebra. Prentice Hall.
- Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
- Zapata, f. 4 maneiras de resolver uma equação de segundo grau. Recuperado de: Francesphysics.Blogspot.com.
- Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.
- « Estrutura de polímeros adicionais, características, função, usa
- Características e exemplos de motivação intrínseca »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)