Equação de continuidade

Explicamos qual é a equação de continuidade, sua fórmula, aplicações, exemplos e propomos exercícios para resolver

Qual é a equação de continuidade?

O equação de continuidade, Para o fluido incompressível, estabelece que a massa total de um fluido que circula através de um tubo, sem perda ou lucro, permanece constante. Em outras palavras, a massa é preservada sem mudanças à medida que o fluido se move.

Um fluido incompressível é que cuja densidade permanece aproximadamente constante enquanto flui. Por exemplo, a água é um líquido considerado incompressível sob condições de pressão e temperatura padrão.

Existe uma maneira matemática de expressar a conservação da massa, na equação de continuidade, dada por:

PARA₁∙ v₁ = A₂∙ v₂

Onde V₁ e V₂ Eles representam a velocidade do fluido em duas seções de um tubo, enquanto₁ já₂ Eles são as respectivas áreas transversais -seccionais.

O produto da área transversal -seccional por velocidade é chamada fluxo E a equação de continuidade implica que, em todo o tubo, o fluxo é constante. O fluxo também é conhecido como taxa de fluxo de volume, É entendido pela observação cuidadosa da expressão anterior, cujas dimensões são volume por unidade de tempo.

Fórmula

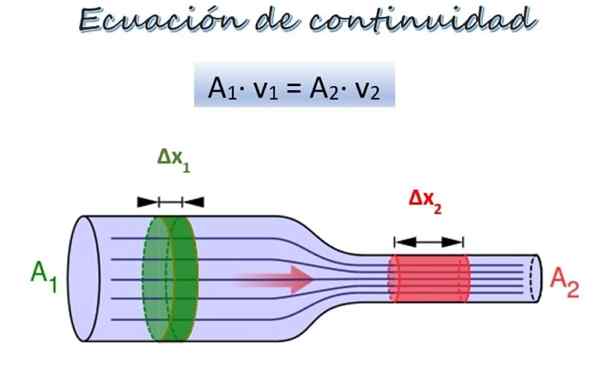A equação de continuidade para o fluxo de um fluido ao longo de um tubo de diferentes diâmetros. Fonte: Wikimedia Commons/F. Zapata.

Na imagem superior, há um tubo com duas seções de diâmetro diferente e na mesma altura, embora possam estar em alturas diferentes sem representar um problema.

Na seção 1, mais largo, a área de seção transversal é para₁ e o fluido se move com velocidade V₁, Enquanto na Seção 2, mais estreito, a área de seção cruzada é para₂ e a velocidade do fluido é V₂.

Uma porção de massa Δm₁ (verde) se move pela Seção 1 em um tempo Δt. Durante esse período, a parte Δm₂ (vermelho) viajar pela Seção 2. Como o fluido é incompressível, sua densidade é a mesma em todos os seus pontos; portanto, a partir da definição de densidade:

Pode servir a você: Gase Constant: O que é, cálculo e exemplos

Aqui ρ é densidade, M é o volume de massa e V. De acordo com isso, a massa ΔM₁ É igual a:

Δm₁ = ρ ∙ V₁

Onde volume v₁ É o produto entre a seção transversal e a distância Δx₁:

Δm₁ = ρ ∙ (A₁ ∙ Δx₁)

Mas desde:

Então a parte da massa Δm₁ Você pode escrever, em termos de velocidade e tempo Δt como:

Δm₁ = ρ ∙ A₁ ∙ Δx₁ = ρ ∙ A₁ ∙ (v₁ ∙ Δt)

Analógico A parte Δm está escrita₂ que flui ao mesmo tempo até a Seção 2:

Δm₂ = ρ ∙ A₂ ∙ Δx₂ = ρ ∙ A₂ ∙ (v₂ ∙ Δt)

Por conservação da missa:

Δm₁ = Δm₂

E:

ρ ∙ a₁ ∙ v₁ ∙ Δt = ρ ∙ a₂ ∙ v₂ ∙ Δt

Como Δt e ρ são cancelados, resultados:

PARA₁ ∙ v₁ = A₂ ∙ v₂

O fluxo q

O produto da seção transversal A pela velocidade do fluido V é chamado de fluxo e denota como q. É equivalente ao volume de fluido por unidade de tempo através do tubo ou vazão de volume:

 V volume e Δt o intervalo de tempo. A vazão no sistema internacional de unidades é M³/s, embora pés cúbicos, galões/min, galões/s a litros/s e galões/s são frequentes. Alguns dos fatores de conversão mais usados ​​são os seguintes:

• 1 m³/S = 264.172 gal/s
• 1 l/s = 0.001 m³/s
• 1 ft³/S = 0.0283168 m³/s
• 1 l/s = 0,264172 gal/s
• 1 m³/S = 15850,3 gal/min

Observe que, diminuindo a seção transversal do tubo, a velocidade do fluido aumenta e vice -versa, se a seção transversal aumentar, a velocidade diminui para que o fluxo seja constante.

Aplicações e exemplos

A equação de continuidade é usada na análise do fluxo do fluido, em combinação com a equação de Bernoulli, na qual as variações da velocidade do fluido nas diferentes seções são levadas em consideração, bem como as mudanças de pressão e o efeito da altura.

Pode atendê -lo: corrente direta

Exemplo 1

Na mangueira do jardim da família, quando a água normalmente sai, o jato tem um certo alcance, mas se colocar o dedo na saída da mangueira, reduzindo o orifício de saída, o alcance do jato é maior é.

Aqui a equação de continuidade é cumprida, pois, diminuindo a área do bico de saída, a velocidade do jato aumenta para que a área de velocidade por velocidade seja constante.

Exemplo 2

O jato de água se estreita quando cai, uma vez que sua velocidade aumenta. Dessa maneira, a velocidade do produto por área permanece constante

Outro exemplo em que a equação de continuidade é destacada é o jato de água que se estreita quando ela cai, devido ao aumento da velocidade da água durante o outono.

Dessa maneira, o fluxo é constante, enquanto o jato continua a fluir em um regime laminar, ou seja, a água cai suavemente sem turbulência ou redemoinhos.

Exercícios resolvidos

Exercício 1

A água circula através de um tubo de 20 cm de diâmetro. Sabendo que o fluxo é 2000 l/s, encontre a velocidade da água no tubo.

• Solução

É conveniente expressar tudo em unidades do sistema internacional. Primeiro, a seção transversal do tubo é calculada, lembrando que o raio é metade do diâmetro:

A = π ∙ (d/2)²

D = 20 cm = 0.2 m

Portanto, a área é:

A = π ∙ (d/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

O fluxo é expresso em m³/s com a ajuda do fator de conversão apropriado:

Q = 2000 l/s = 2 m³/s

A partir da fórmula q = a ∙ v a velocidade com que o fluido circula através do tubo é limpo:

Exercício 2

Você tem um tubo de seção cruzado variável através do qual a água flui. Em um certo ponto, a seção transversal é 0.070 m² E a velocidade da água é 3.50 m/s. Calcular:

Pode servir a você: Pascal Princípio: História, Aplicações, Exemplos

a) A velocidade da água em outro ponto no tubo cuja área de seção transversal é 0.105 m².

b) o volume de água que é descarregado por uma extremidade aberta em 1 hora.

• Solução para

A equação de continuidade é usada, correspondendo ao fluxo do primeiro ponto com o fluxo do segundo. O fluxo é:

Q = A ∙ V

Para continuidade:

Q₁ = Q₂

PARA₁ ∙ v₁ = A₂ ∙ v₂

Agora eles substituem os dados fornecidos pela declaração:

• PARA₁ = 0.070 m²
• v₁ = 3.50 m/s
• PARA₂ = 0.105 m²
• v₂ =?

E limpa v₂:

Solução b

Como o fluxo também é o volume por unidade de tempo, ele precisa:

Portanto, o volume V é:

V = q ∙ Δt = (a ∙ v) Δt

O fluxo que pode ser calculado com os dados do ponto 1 ou o do ponto 2, pois é o mesmo nos dois pontos:

Q = a₁ ∙ v₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / s

Sabendo que 1 hora = 3600 s, o volume de água descarregado é:

V = q ∙ Δt = (0.245 m³ / s) × (3600 s) = 882 m³

Em 1 hora 882 m são baixados³ de água através do cano.