Conceito de distância euclidiana, fórmula, cálculo, exemplo

O Distância euclidiana É um número positivo que indica a separação que dois pontos têm em um espaço onde os axiomas e os teoremas da geometria da Euclides são atendidos.

A distância entre dois pontos A e B de um espaço euclidiano é o comprimento do vetor Ab Pertencente à única linha que passa por esses pontos.

figura 1 . Espaço euclidiano unidimensional formado pela linha (OX). Vários pontos neste espaço, suas coordenadas e distâncias são mostradas. (Preparado por Ricardo Pérez).

O espaço que percebemos e onde movemos os seres humanos é um espaço tridimensional (3-D), onde os axiomas e os teoremas da geometria de euclídeo são cumpridos. Neste espaço, há subespaços (planos) bilimensionais e um subespaço (reto) (reto) (reto).

Os espaços euclidianos podem ser de uma dimensão (1-D), duas dimensões (2-D), três dimensões (3-D) ou N dimensões (N-D).

Estes são pontos no espaço único -dimensional x que pertencem à linha orientada (OX), a direção de ou para x é o endereço positivo. Para localizar os pontos nesta linha, o sistema cartesiano que consiste em atribuir cada ponto da linha é usado um número.

[TOC]

Fórmula

A distância euclidiana d (a, b) é definida entre os pontos A e B, localizados em uma linha, como a raiz quadrada do quadrado das diferenças de suas coordenadas x:

D (a, b) = √ ((xb - xa)^2)

Esta definição garante que: a distância entre dois pontos é sempre uma quantidade positiva. E que a distância entre A e B é igual à distância entre B e A.

A Figura 1 mostra o espaço euclidiano único -dimensional formado pela linha (OX) e vários pontos nessa linha. Cada ponto tem uma coordenada:

O ponto A tem coordenada XA = 2.5, a coordenada B Xb = 4 e o ponto C coordenam xc = -2.5

Pode servir a você: probabilidade de frequência: conceito, como é calculado e exemplos

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Distância euclidiana em duas dimensões

O espaço de euclídeo bilimensional é um avião. Os pontos de um plano euclidiano atendem aos axiomas da geometria da Euclides, por exemplo:

- Em dois pontos, uma única linha passa. 

- Três pontos no plano formam um triângulo cujos ângulos internos sempre adicionam 180º.

- Em um triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados de suas pernas.

Em duas dimensões, um ponto tem coordenadas x e y. 

Por exemplo, um ponto P tem coordenadas (XP, YP) ​​e um ponto que coordenou (xq, yq).

A distância euclidiana entre o ponto P e Q é definida com a seguinte fórmula:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Deve -se notar que esta fórmula é equivalente ao teorema de Pitágoras, como mostrado na Figura 2.

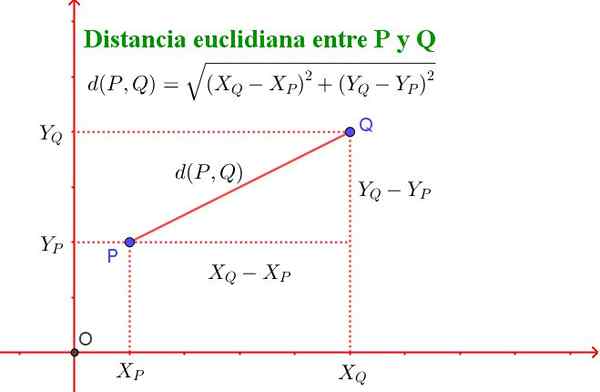Figura 2. A distância entre dois pontos P e Q do avião encontra o teorema de Pitágoras. (Preparado por Ricardo Pérez).

Superfícies não uclidianas

Nem todos os espaços bidimensionais encontram geometria euclidiana. A superfície de uma esfera é um espaço bidimensional.

Os ângulos de um triângulo em uma superfície esférica não adicionam 180º e, com isso, o teorema de Pitágoras não é cumprido; portanto, uma superfície esférica não cumpre os axiomas da Euclides.

Distância euclidiana em n dimensões

O conceito de coordenadas pode ser estendido a maiores dimensões:

- No ponto 2-D, P tem coordenadas (XP, YP)

- Em 3-D, um ponto que tem coordenadas (xq, yq, zq)

- No ponto 4-D, R terá coordenadas (XR, YR, ZR, WR)

- Em N-D, um ponto P terá coordenadas (P1, P2, P3, ..., PN)

Pode servir a você: Bars Gráfico: Características, para que serve, exemplos

A distância entre dois pontos P e Q de um espaço euclidiano N-dimensional é calculada com a seguinte fórmula:

D (p, q) = √ ((Q1 - P1)^2 +(Q2 - P2)^2 +… +(qn - pn)^2)

O local geométrico de todos os pontos que em um espaço euclidiano N-dimensional que os equidistas de outro ponto p fixo (o centro) formam uma hipersferência n-dimensional.

Como calcular a distância euclidiana

Abaixo está a distância entre dois pontos localizados no espaço tridimensional euclidiano é calculado.

Assuma o ponto A das coordenadas cartesianas x, y, z dada por a :( 2, 3, 1) e o ponto B das coordenadas b :( -3, 2, 2).

Você deseja determinar a distância entre esses pontos, para os quais o relacionamento geral é usado:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5.196

Exemplo

Existem dois pontos P e q.  O ponto p para as coordenadas cartesianas x, y, z dada por p :( 2, 3, 1) e o ponto Q das coordenadas Q :( -3, 2, 1).

É solicitado a encontrar as coordenadas do ponto médio M do segmento [PQ] que conecta os dois pontos. 

Solução:

Supõe -se que o ponto desconhecido m tenha coordenadas (x, y, z).

Como m é o ponto médio de [PQ], deve -se cumprir que D (p, m) = d (q, m), portanto também deve ser cumprido d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Como neste caso, o terceiro termo é o mesmo nos dois membros que a expressão anterior é simplificada para:

Pode atendê -lo: constante absoluta

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Há então uma equação com dois incógnitas x e y. Outra equação é necessária para resolver o problema.

O ponto M pertence à linha que passa pelos pontos P e Q, que podemos calcular o seguinte:

Primeiro é o vetor do diretor Pq da linha: Pq = = .

Então PM = Op + para Pq, onde Op É a posição vetorial do ponto P e para É um parâmetro que pertence a números reais. 

A equação anterior é conhecida como a equação vetorial da linha, que nas coordenadas cartesianas adota da seguinte forma:

= + a =

Iguais Os componentes correspondentes são:

X - 2 = 2 - 5 A; E - 3 = 3 -a; Z - 1 = 0

Ou seja, x = 4 - 5a, y = 6 - a, finalmente z = 1.

É substituído na expressão quadrática que relaciona x a y:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - a - 2)^2

É simplificado:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Agora se desenvolve:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

É simplificado, cancelando termos semelhantes nos dois membros:

4 - 20A + 9 - 6A = 49 - 70A + 16 - 8A

Parâmetro A:

52 a = 49 + 16 - 4 - 9 = 52 resultando que a = 1.

Isto é, que x = 4 - 5, y = 6 - 1, finalmente z = 1.

Finalmente, obtemos as coordenadas cartesianas do ponto médio M do segmento [PQ]:

M: (-1, 5, 1).

Referências

1. Lehmann c. (1972) Geometria analítica. Uteha.
2. Superprof. Distância entre dois pontos. Recuperado de: superprof.é
3. Unam. Distância entre variedades sublineares relacionadas. Recuperado de: Prometheus.Matem.Unam.mx/
4. Wikipedia. Distância euclidiana. Recuperado de: é.Wikipedia.com
5. Wikipedia. Espaço euclidiano. Recuperado de: é.Wikipedia.com