Símbolos e fórmulas de diâmetro, como retirá -lo, circunferência

Ele diâmetro É a linha reta que passa pelo centro de uma curva plana fechada ou uma figura em duas ou três dimensões e que também se junta a seus pontos opostos. Geralmente é um círculo (uma curva plana), um círculo (uma figura plana), uma esfera ou um cilindro circular reto (objetos tridimensionais).

Embora a circunferência e o círculo sejam geralmente tomados como sinônimos, há uma diferença entre os dois termos. A circunferência é a curva fechada que se envolve ao círculo, que atende à condição de que a distância entre qualquer um de seus pontos e o centro seja a mesma. Esta distância não é outra senão o raio da circunferência. Em vez disso, o círculo é uma figura plana limitada pela circunferência.

figura 1. O diâmetro das rodas de bicicleta é uma característica importante em seu design. Fonte: Pixabay.

Em caso de circunferência, círculo e esfera, o diâmetro é um segmento reto que contém pelo menos três pontos: o centro mais dois pontos da borda da circunferência ou círculo, ou a superfície da esfera.

E quanto ao cilindro circular reto, o diâmetro refere -se à seção transversal, que junto com a altura, são seus dois parâmetros característicos.

O diâmetro da circunferência e do círculo, simbolizado por Ø ou simplesmente a letra "d" ou "d", está relacionada ao seu perímetro, contorno ou comprimento, que é indicado com a letra L:

L = π.D = π. qualquer

Sempre que você tem uma circunferência, o quociente entre seu comprimento e seu diâmetro é o número irracional π = 3.14159 ... dessa maneira:

π = l/d

[TOC]

Como obter o diâmetro?

Quando o desenho da circunferência ou círculo está disponível, ou diretamente o objeto circular, como uma moeda ou um anel, por exemplo, é muito fácil tomar o diâmetro com uma regra. Você simplesmente precisa garantir que a borda da regra ao mesmo tempo tenha dois pontos da circunferência e o centro do mesmo.

Pode servir você: algébrica

Um calibre, vernier ou rei do rei é muito adequado para medir diâmetros externos e internos em moedas, argolas, anéis, nozes, tubos e muito mais.

Figura 2. Vernier Digital medindo o diâmetro de uma moeda. Fonte: Pixabay.

Se, em vez de o objeto ou seu desenho, você tem dados como o rádio R, Em seguida, multiplicando por 2 você tem o diâmetro. E se o comprimento ou perímetro da circunferência for conhecido, o diâmetro também pode ser conhecido, por autorização:

D = 2.R
D = l / π

Outra maneira de obter o diâmetro é conhecer a área do círculo, a superfície esférica, a seção transversal do cilindro, a área curva deste ou dos volumes da esfera ou do cilindro. Tudo depende de qual figura geométrica é. Por exemplo, o diâmetro está envolvido nas seguintes áreas e volumes:

-Área circular: π.(D/2)²
-Área de superfície esférica: 4π.(D/2)²
-Volume da esfera: (4/3) π.(D/2)³
-Volume de cilindro circular reto: π.(D/2)².H (h é a altura do cilindro)

Figuras de constante larga

O círculo é uma figura plana de constante larga, pois onde quer que pareça, a largura é diâmetro d. No entanto, existem outras figuras talvez menos conhecidas cuja largura também é constante.

Primeiro, vamos ver o que é entendido pela largura de uma figura: é a distância entre duas linhas paralelas -suponha Remes -que, por sua vez, são perpendiculares à direção dada e que aprisionam a figura, como mostrado na imagem esquerda:

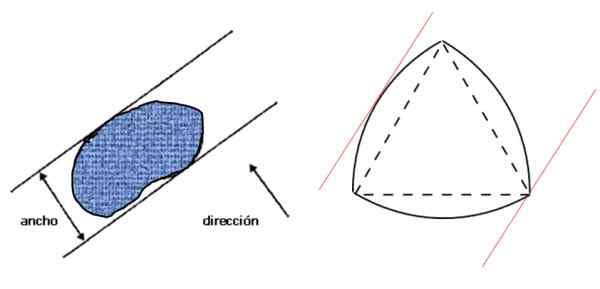Figura 3. Largura de qualquer figura plana (esquerda) e Triângulo Reuleaux, uma figura larga constante (direita). Fonte: f. Zapata.

Então, à direita, é o triângulo Reuleaux, que é uma figura ampla constante e que atende à condição especificada na figura esquerda. Se a largura da figura for D, seu perímetro é dado pelo teorema de Barbier:

Pode servir a você: Medição aproximada de figuras amorfas: Exemplo e exercício

L = π.D

Os esgotos da cidade de São Francisco, na Califórnia, são moldados como o triângulo de Reuleaux, nomeado pelo engenheiro alemão Franz Reuleaux (1829 - 1905). Dessa maneira, as tapas não podem cair no buraco e gastar menos material para fabricá -las, porque sua área é menor que a do círculo:

A = (1- √3).πd² = 0.705.D²

Enquanto estiver para um círculo:

A = π.(D/2)² = (π/4) D²= 0.785.D²

Mas este triângulo não é a única figura constante larga. Chamadas podem ser construídas Reuleaux Polgons com outros polígonos que têm um número de lados estranhos.

Diâmetro de uma circunferência

Na figura seguinte estão os elementos da circunferência, definidos da seguinte forma:

Corda: segmento de linha que se junta a dois pontos da circunferência. Na figura está a corda que se junta aos pontos C e D, mas as cordas infinitas podem ser rastreadas para que qualquer outro ponto da circunferência.

Diâmetro: É a corda que passa pelo centro, juntando dois pontos da circunferência com o centro ou. É a corda mais longa de uma circunferência, por esse motivo, é chamado de "corda principal".

Rádio: segmento de linha que se junta ao centro com qualquer ponto da circunferência. Seu valor, como o diâmetro, é constante.

Circunferência: É o conjunto de todos os pontos que equivale ou.

Arco: É definido como um segmento de circunferência delimitado por dois rádios (não desenhados na figura).

Figura 4. Partes da circunferência, incluindo o diâmetro, que passa pelo centro. Fonte: Wikimedia Commons.

- Exemplo 1

O retângulo mostrado mede 10 polegadas de altura, que, ao enrolamento, forma um cilindro circular reto cujo diâmetro é de 5 polegadas. Responda as seguintes questões:

Pode atendê -lo: eventos mutuamente exclusivos: propriedades e exemplos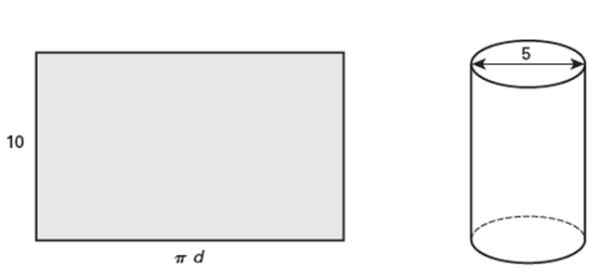Figura 5. Um retângulo enrolado se torna um cilindro circular reto. Fonte: Jiménez, R. Matemática II. Geometria e trigonometria. 2º. Edição. Pearson.

a) Qual é o contorno do tubo?
b) Encontre a área do retângulo
c) Calcule a área de seção cruzada do cilindro.

Solução para

O contorno do tubo é l = π.D = 5π plg = 15.71 PLG.

Solução b

A área do retângulo é Base x altura, sendo a base L já calculada e a altura é 10 PLG de acordo com a declaração, portanto:

A = 15.71 plg x 10 plg = 157.1 plg².

Solução c

Finalmente, a área solicitada é calculada da seguinte maneira:

A = π.(D/2)² = (π/4) D² = (π/4) x (5 plg)²= 19.63 plg².

- Exemplo 2

Calcule a área sombreada da Figura 5A. O quadrado tem lado l.

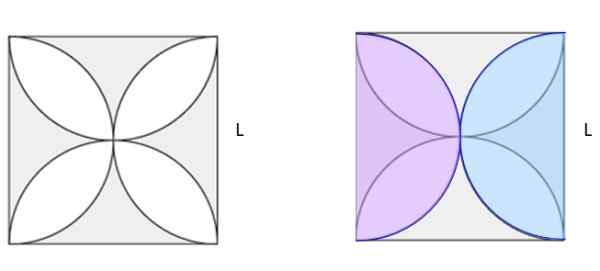Figura 6. Encontre a área sombreada na figura esquerda. Jiménez, r. Matemática II. Geometria e trigonometria. 2º. Edição. Pearson.

Solução

Na Figura 5b, dois semicírculos idênticos de tamanho em cores rosa e azul foram desenhados, sobrepostos na figura original. Entre eles, eles fazem um círculo completo. Se o quadrado do quadrado for calculado e a área do círculo for subtraída, ele torna a área sombreada da Figura 5b. E parecendo bem, acontece que é metade da área sombreada em 5a.

-Quadrado da área: L²
-Diâmetro semi -círculo: l
-Área de círculo: π.(L/2)²= (π/4) l²
-Diferença de áreas = metade da área sombreada =

eu² - (π/4) l² = [(4 - π)/4] L²= 0.2146 l²

-Área sombreada = 2 x 0.2146 l²= 0.4292L2

Quantos diâmetros uma circunferência tem?

Diâmetros infinitos podem ser desenhados em um círculo, e qualquer um deles mede o mesmo.

Referências

1. Antonio. Triângulos de Reuleaux e outras curvas de largura constantes. Recuperado de: disseminadores.com.
2. Baldor, a. 2002. Geometria plana e espacial e trigonometria. Grupo de pátria cultural.
3. Jiménez, r. Matemática II. Geometria e trigonometria. 2º. Edição. Pearson.
4. Wikipedia. Triângulo de Reuleaux. Recuperado de: é.Wikipedia.org.
5. Wolfram Mathworld. Diâmetro. Recuperado de: Mathworld.Volfrâmio.com.