Diferenças entre velocidade e velocidade (com exemplos)

As diferenças entre velocidade e velocidade Existem, embora ambos sejam quantidades físicas relacionadas. Na linguagem comum, um termo ou outro é usado de forma intercambiável como se fossem sinônimos, mas na física é necessário distingui -los.

Neste artigo, ambos os conceitos são definidos, as diferenças são indicadas e explicadas, por exemplos, como e quando um ou outro se aplica. Para simplificar, consideramos uma partícula em movimento e, a partir daí, analisaremos os conceitos de velocidade e velocidade. 

	Velocidade	Velocidade
Definição	É a distância percorrida por unidade de tempo.	É o deslocamento (ou mudança de posição) em cada unidade de tempo.
Notação	v	v
Tipo de objeto matemático	Escalar.	Vetor.
Fórmula (por um período de tempo finito)*	v = ΔS/Δt	v = ΔR/Δt
Fórmula (por um instante de tempo) **	v = ds/dt = s '(t)	v = dr/dt = r '(t)
Explicação da fórmula	*Duração do caminho percorrido dividido entre o período usado para viajá -lo.** Na velocidade instantânea, o tempo de tempo tende a zero. ** A operação matemática é o derivado do arco de trajetória em função do tempo em relação ao tempo t do tempo.	*Deslocamento vetorial dividido pelo período de tempo em que o deslocamento ocorreu. ** Na velocidade instantânea, o período tende a zero. ** A operação matemática é a derivada da posição no prazo.
Caracteristicas	Para expressá -lo, apenas um número real positivo é necessário, independentemente das dimensões espaciais em que o movimento ocorre. ** A velocidade instantânea é o valor absoluto da velocidade instantânea.	Mais de um número real (positivo ou negativo) pode ser necessário para expressá -lo, dependendo das dimensões espaciais em que o movimento ocorre. ** O módulo de velocidade instantâneo é instantaneamente.

Exemplos com rapidez uniforme em seções retas

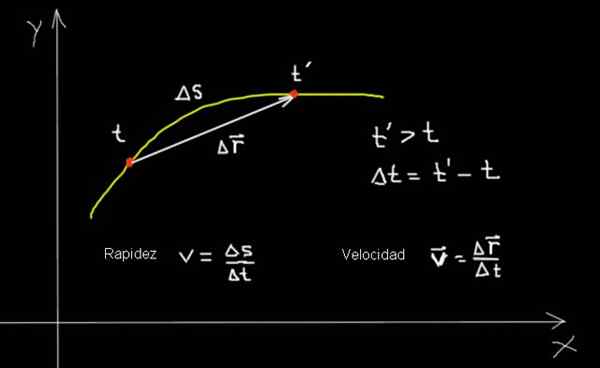
Velocidade e velocidade de uma partícula que se move em uma curva. Preparado por: f. Zapata.

Na tabela anterior, vários aspectos de velocidade e velocidade foram resumidos. E então, para complementar, são considerados vários exemplos que ilustram os conceitos envolvidos e seus relacionamentos:

Pode atendê -lo: paramagnetismo

- Exemplo 1

Suponha que uma formiga vermelha se mova após uma linha reta e na direção indicada na figura a seguir.

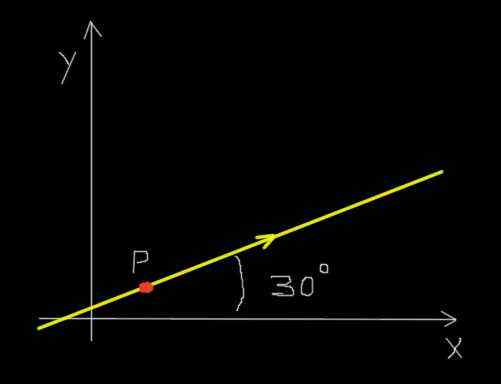Uma formiga no caminho retilineal. Fonte: f. Zapata.

Além disso, a formiga se move uniformemente para percorrer uma distância de 30 milímetros em um período de 0,25 segundos. 

Determinar a velocidade e velocidade da formiga.

Solução 

A velocidade da formiga é calculada dividindo a distância ΔS Toure Tour Δt.

V = ΔS/ΔT = (30 mm)/(0,25s) = 120 mm/s = 12 cm/s

A taxa da formiga é calculada dividindo o deslocamento Δr entre o período em que o referido deslocamento foi feito.

O deslocamento foi de 30 mm na direção 30º em relação ao eixo x, ou em uma forma compacta: 

Δr = (30 mm 000)

Pode -se notar que o deslocamento consiste em uma magnitude e um endereço, pois é uma quantidade vetorial. Como alternativa, o deslocamento pode ser expresso de acordo com seus componentes cartesianos X e Y, desta maneira:

Δr = (30 mm* cos (30º); 30 mm* sem (30º)) = (25,98 mm; 15,00 mm)

A taxa da formiga é calculada dividindo o deslocamento entre o período em que foi realizado:

v = Δr/Δt = (25,98 mm / 0,25 s; 15,00 mm / 0,25 s) = (103,92; 60,00) mm / s

Essa velocidade nos componentes cartesianos x e y y em unidades de cm/s é:

v = (10.392; 6.000) cm/s.

Como alternativa, o vetor de velocidade pode ser expresso em sua forma polar (módulo… direção) como mostrado:

v = (12 cm/s · 30º).

Observação: Neste exemplo, pois a velocidade é constante, a velocidade média e a velocidade instantânea coincidem. Está provado que o módulo de velocidade instantâneo é instantâneo rápido.

Pode atendê -lo: densidade

Exemplo 2

A mesma formiga do exemplo anterior vai de A a B, depois de B a C e finalmente de C a A, seguindo o caminho triangular mostrado na figura a seguir.

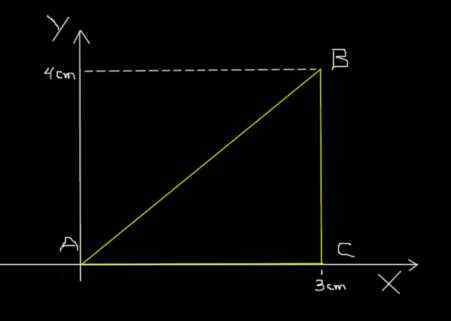Caminho triangular de uma formiga. Fonte: f. Zapata.

A seção AB viaja a 0,2s; O BC viaja a 0,1s e, finalmente, a CA viaja a 0,3s. Calcule a velocidade média da rota ABCA e a velocidade média da rota ABCA.

Solução 

Para calcular a velocidade média da formiga, começamos determinando a distância total percorrida:

ΔS = 5 cm + 4 cm + 3 cm = 12 cm.

O período usado para toda a jornada é:

Δt = 0,2s + 0,1s + 0,3s = 0,6 s.

Então, a velocidade média da formiga é:

V = ΔS/ΔT = (12 cm)/(0,6s) = 20 cm/s.

Então a velocidade média da formiga na rota da ABCA é calculada. Nesse caso, o deslocamento feito pela formiga é:

ΔR = (0 cm; 0 cm)

Isso ocorre porque o deslocamento é a diferença entre a posição final menos a posição inicial. Como ambas as posições são iguais, então a diferença é nula, resultando em um deslocamento nulo.

Esse deslocamento nulo foi realizado em um período de 0,6s, de modo que o tipo médio de formiga era:

v =(0 cm; 0 cm)/ 0,6s = (0; 0) cm/ s.

Conclusão: Velocidade média 20 cm/s, Mas a velocidade média é zero na rota da ABCA.

Exemplos com rapidez uniforme em seções curvas

Exemplo 3

Um inseto se move em um círculo de raio de 0,2m com velocidade uniforme, de modo que, a partir de A e atingindo B, ele viaja ¼ de circunferência a 0,25 s.

Pode servir a você: imprensa hidráulica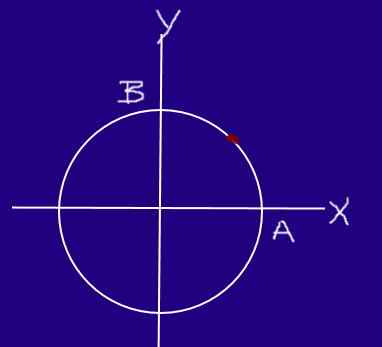Seção circular inseto. Fonte: f. Zapata.

Determine a velocidade e a velocidade do inseto na seção AB.

Solução 

O comprimento do arco de circunferência entre A e B é:

ΔS = 2πr /4 = 2π (0,2m) /4 = 0,32 m.

Aplicando a definição de velocidade média que você tem:

V = ΔS/ΔT = 0,32 m/0,25 s = 1,28 m/s.

Para calcular a velocidade média, é necessário calcular o vetor de deslocamento entre a posição inicial A e o B final:

Δr = (0; r)-(r; 0) = (-r; r) = (-0,2; 0,2) m

Aplicando a definição média de velocidade é obtida:

v = Δr/ Δt = (-0,2; 0,2) m / 0,25s = (-0.8; 0,8) m/s.

A expressão anterior é a velocidade média entre A e B expressa em forma cartesiana. Como alternativa, a velocidade média pode ser expressa em forma polar, ou seja, módulo e direção:

| v | = ((-0,8)^2 + 0,8^2)^(½) = 1,13 m/s

Endereço = arctan (0,8 / (-0,8)) = arcan (-1) = -45º + 180º = 135º em relação ao eixo x.

Finalmente, o vetor de velocidade média na forma polar é: v =(1,13 m/s 000 135º).

Exemplo 4

Supondo que o momento inicial do inseto do exemplo anterior seja 0s do ponto A, sua posição de vetor é, em um instante, qualquer t é dado por:

r(t) = [r cos ((π/2) t); R sen ((π/2) t)].

Determine a velocidade e a velocidade instantânea para qualquer momento t.

Solução 

A velocidade instantânea é o derivado em relação ao tempo da posição:

v(t) = Dr/dt = [-r (π/2) sem ((π/2) t); R (π/2) cos ((π/2) t)]]

A velocidade instantânea é o módulo da velocidade instantânea do vetor:

v (t) = | v(T) | = π r / 2^½

Referências

1. Alonso m., Finn e. Volume da física I: mecânica. 1970. Fundo Educacional Inter -Americano.PARA.
2. Hewitt, p. Ciência física conceitual. QUINTA EDIÇÃO. Pearson.
3. Jovem, Hugh. Física da Universidade com Física Moderna. 14ª ed. Pearson.
4. Wikipedia. Velocidade. Recuperado de: é.Wikipedia.com
5. Zita, a. Diferença entre velocidade e velocidade. Recuperado de: Diferenciador.com