Diferença entre círculo e circunferência (com exemplos)

O Diferença entre círculo e circunferência É o seguinte: o círculo é uma superfície plana, contornada ou delimitada por um círculo, enquanto o último é uma curva plana.

Freqüentemente, ambos os conceitos estão confusos, pois estão relacionados, mas você sempre precisa se lembrar que a circunferência é a borda do círculo, enquanto contém a circunferência e todos os pontos.

Ambos têm muitos elementos em comum, como o centro, o raio e o diâmetro, entre outros, de acordo com a seguinte tabela comparativa:

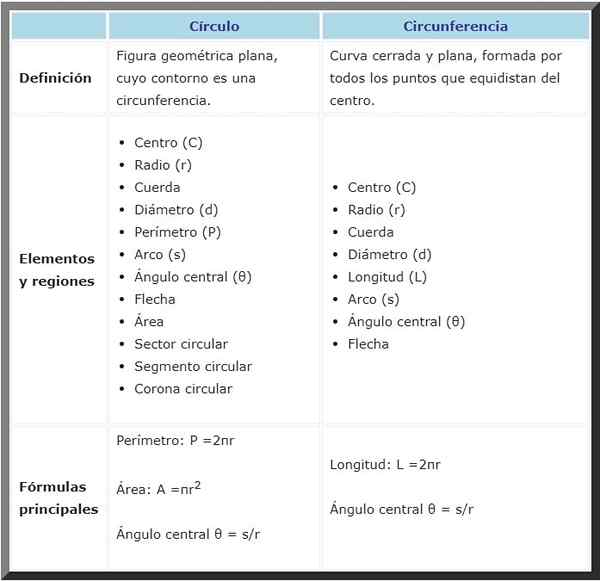
	Círculo	Circunferência
Definição	Figura geométrica plana, cujo contorno é uma circunferência.	Curva fechada e plana, formada por todos os pontos que são equidististas no centro.
Elementos e regiões	Centro (c) Rádio (R) Corda Diâmetro (D) Perímetro (P) Arco (s) Ângulo central (Θ) Seta Área Setor circular Segmento circular Coroa circular	Centro (c) Rádio (R) Corda Diâmetro (D) Comprimento (l) Arco (s) Comprimento central (Θ) Seta
Fórmulas	Perímetro: p = 2π⋅r Área: a =πR2 Ângulo central: Θ= s/r	Comprimento: L = 2π⋅r Ângulo central: Θ= s/r

[TOC]

Círculo: Definição, Características e Peças

Um círculo é uma figura geométrica plana, que inclui todos os pontos da circunferência que forma o contorno e também todos os pontos interiores.

Por esse motivo, é caracterizado por ter:

-Borda ou perímetro, que é a circunferência do círculo.

-Uma área superficial.

Os elementos do círculo

Cada círculo tem as seguintes partes ou elementos:

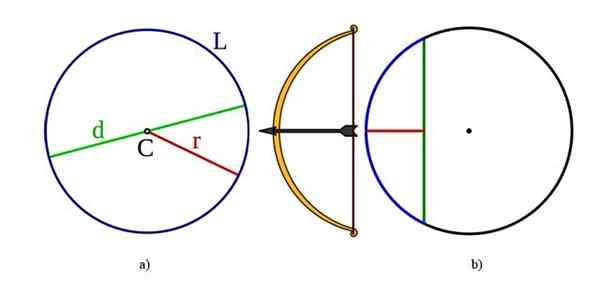Os elementos do círculo, também comuns à circunferência: à esquerda em a) são o centro d, diâmetro d, raio r e comprimento l l l l l l l l l l l l l l. Bem em b) há a corda e sagita ou flecha. Fonte: Wikimedia Commons.

Centro: O que é o ponto C, que equidistas todos os pontos da borda.

Pode atendê -lo: arco (geometria): medida, tipos de arcos, exemplos

Corda: segmento que se junta a dois pontos da borda do círculo. Na Figura B) à direita, é o segmento verde mais escuro.

Diâmetro: segmento verde mais claro, denotado "d" na Figura A), que se junta a dois pontos da borda e, ao mesmo tempo, passa pelo centro. O diâmetro também é uma corda, a mais longa de todos, por isso é conhecida como o Corda principal.

Rádio: denotado por "r" na figura a), é o segmento vermelho que se junta ao centro do círculo com um ponto da borda. Sua medida é metade do diâmetro.

Arco: uma parte do contorno que está entre dois pontos disso, em azul na Figura B).

Ângulo central: É o ângulo cujo vértice está no centro ou e os lados são rádios do círculo.

Seta: segmento perpendicular a uma corda (em vermelho na Figura B), que se junta ao centro da corda com um ponto da borda.

Comprimento ou perímetro: É a medida do contorno do círculo, denotado l. Depende da Rádio R e é proporcional ao número irracional π:

π = 3.1416 ..

De maneira que:

L = 2π⋅r

Regiões circulares

Sendo uma figura plana, o círculo tem uma área total e também várias regiões. Os mais conhecidos são os seguintes:

Área circular: É proporcional ao quadrado do raio, a constante de proporcionalidade sendo o número π.

Chamando a área do círculo, é expressa como:

A = πr²

Segmento circular: É uma parte do círculo limitada pelo arco azul e pela corda verde escura na Figura B.

Pode servir a você: ângulos suplementares: o que são, cálculo, exemplos, exercícios

Setor circular: É também uma região do círculo, mas continha entre dois rádios e o arco correspondente.

Coroa circular: É moldado como um anel e é limitado por duas circunferências concêntricas, fora do de Radio Menor e dentro do prefeito de rádio.

Circunferência: dEfinição, características e peças 

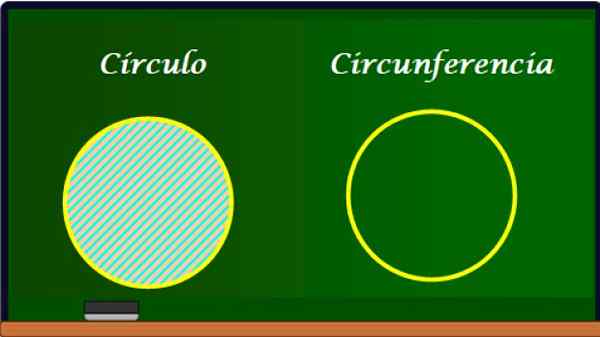Um círculo e sua circunferência. Fonte: f. Zapata.

A circunferência é a borda do círculo e, portanto, tem muitos elementos em comum com este. No entanto, a circunferência não tem área, porque, como é uma curva, só tem comprimento l.

A circunferência é formalmente definida como o conjunto de todos os pontos que equivalem a de outro ponto conhecido como o centro.

Os pontos internos não estão incluídos, pois eles correspondem ao círculo.

Os elementos da circunferência

Muitos dos elementos da circunferência são os mesmos que os do círculo, excluindo aqueles que se referem a áreas e regiões, de modo que a figura superior serve como uma referência.

Temos então:

Centro: denotado por c e às vezes também como o, todos os pontos da circunferência mantêm a mesma distância.

Corda: segmento que se junta a dois pontos pertencentes à circunferência.

Diâmetro: Também se junta a dois pontos da circunferência, mas sempre passa pelo centro do mesmo.

Rádio: É a distância entre o centro e qualquer ponto da circunferência.

Arco: É uma parte da circunferência.

Ângulo central: É o ângulo com o vértice no centro C e dois lados iguais que medem como o rádio.

Seta: segmento perpendicular a uma corda, que se junta ao centro disso com o ponto correspondente da circunferência.

Pode servir a você: Princípio multiplicativo: Técnicas e exemplos de contagem

Comprimento ou perímetro: É a medida da circunferência que, como vimos, é proporcional ao número π = 3.1416 ... e é calculado pela fórmula:

L = 2π⋅r

A equação da circunferência

Um ponto P pertence a uma circunferência, desde que sua distância a outro ponto C seja igual a r, o rádio.

Qualquer ponto no avião cartesiano tem coordenadas (X, y) e o quadrado de distância d Entre dois deles, P₁(x₁,e₁) E P₂(x₂,e₂), é dado pela fórmula:

d₂² = (x₂ - x₁)² +  (e₂ - e₁)²

Vamos levar ao ponto das coordenadas (x, y) e para coordenar o ponto C (H, K). Substituindo, a equação anterior seria assim:

(X - h)² +  (e que)² = r²

Esta é a equação de circunferência, que qualquer ponto nela satisfaz. Se o centro da circunferência estiver coincidindo com a origem do sistema de coordenadas, então h = k = 0 e a equação será simplificada:

x² + e² = r²

Vejamos um exemplo de como usar a equação e responder a esta questão: o ponto (4.6) pertence à circunferência (x - 1)² +  (e - 2)² = 25?

Para descobrir as coordenadas do ponto da equação, são substituídas e, se for uma igualdade, o ponto pertence à circunferência:

(4 - 1)² +  (6 - 2)² = 3² + 4² = 9 + 16 = 25

E de fato, como 25 = 25, conclui -se que (4.6) pertence à circunferência.

Referências

1. Tutoriais de matemática gratuitos. Área e perímetro de um círculo - calculadora de geometria. Recuperado de: analisath.com.
2. Math Open Reference. Circunferência, perímetro de um círculo. Recuperado de: MathpenRef.com.
3. Cienting. Como encontrar o perímetro de um círculo. Recuperado de: cienting.com.
4. Stewart, J. 2006. Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
5. Zill, d. 1984. Álgebra e trigonometria. McGraw Hill.