Equações de diagrama Moody, para que serve, aplicações

Ele Diagrama Moody Consiste em uma série de curvas desenhadas em papel logarítmico, que são usados ​​para calcular o fator de atrito presente no fluxo de um fluido turbulento através de um duto circular.

Com o fator de atrito F A perda de energia de atrito é avaliada, um valor importante para determinar o desempenho adequado das bombas que distribuem fluidos como água, gasolina, petróleo bruto.

Tubos em nível industrial. Fonte: Pixabay.

Para conhecer a energia no fluxo de um fluido, é necessária e as paredes do tubo.

[TOC]

Equações para a energia de um fluido de movimento

Entre duas seções de um tubo, denotadas como 1 e 2, É possível estabelecer o seguinte saldo, que é uma expansão da equação de Bernoulli: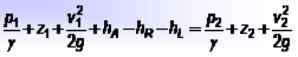Onde:

- p₁ e p₂ são as pressões em cada ponto,

- z₁ e z₂ são as alturas em relação a um ponto de referência,

- v₁ e v₂ são as respectivas velocidades de fluido,

- h_PARA É a energia adicionada pelas bombas, h_R É a energia tomada por um dispositivo como um motor e h_eu Ele cobre as perdas de energia fluida devido ao atrito entre isso e as paredes dos tubos, bem como outras pequenas perdas.

O valor de h_eu É calculado usando a equação de Darcy-Weisbach:

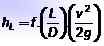
Onde eu É o comprimento do tubo, D É seu diâmetro interno, v É a velocidade do fluido e g É o valor da aceleração da gravidade. As dimensões de h_eu Eles são longos, e geralmente as unidades em que é representada são medidores ou pés.

-Número do fator de atrito e Reynolds

Calcular F Equações empíricas obtidas a partir de dados experimentais podem ser usados. É necessário distinguir se é um fluido no regime laminar ou regime turbulento. Para o regime laminar F É facilmente avaliado:

F = 64/n_R

Onde N_R É o número de Reynolds, cujo valor depende do regime em que o fluido está localizado. Os critérios são:

Fluxo laminar: n_R < 2000 el flujo es laminar; Flujo turbulento N_R > 4000; Regime de transição: 2000 < N_R < 4000

O número de Reynolds (sem dimensão), por sua vez, depende da velocidade do fluido v, O diâmetro interno do oleoduto D e a viscosidade cinemática n do fluido, cujo valor é obtido por tabelas:

Pode servir você: Movimento retilíneo de uniformemente acelerado: características, fórmulas

N_R = v.D /n

Equação de Colebrook

Para um fluxo turbulento, a equação mais aceita nos tubos de cobre e vidro é a de Cyril Colebrook (1910-1997), mas tem a inconveniência de que F Não é explícito:

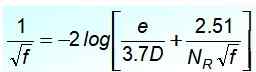
Nesta equação, o quociente e/d É a relativa aspereza do tubo e N_R É o número de Reynolds. Ao observá -lo com cuidado, percebe -se que não é fácil sair F No lado esquerdo da igualdade, portanto não é conveniente para cálculos imediatos.

O próprio Colebrook sugeriu essa abordagem explícita, válida com algumas limitações:

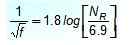
Para que serve?

O diagrama de Moody é útil para encontrar fator de atrito F incluído na equação de Darcy, tendo em vista o fato de que na equação de Colebrook não é fácil expressar F diretamente em termos de outros valores.

Seu uso simplifica a obtenção do valor de F, contendo a representação gráfica de F em função de N_R Para diferentes valores de rugosidade relativa em uma escala logarítmica.

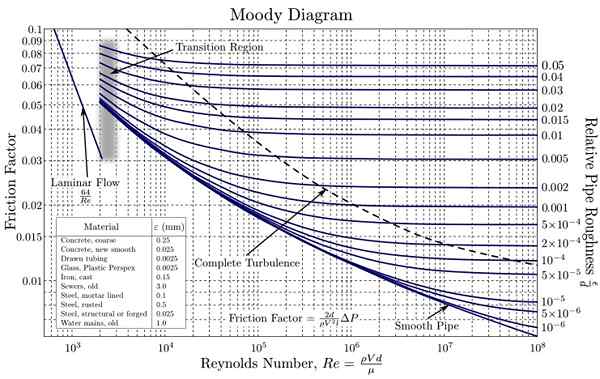Diagrama Moody. Fonte: https: // upload.Wikimedia.org/wikipedia/commons/d/d9/Moody_en.Svg

Essas curvas foram criadas a partir de dados experimentais com vários materiais comumente usados ​​na fabricação de tubos. O uso de uma escala logarítmica para F como para N_R É necessário, pois eles cobrem uma ampla gama de valores. Dessa maneira, o gráfico de valores de diferentes ordens de magnitude é facilitado.

O primeiro gráfico da equação de Colebrook foi obtido pelo engenheiro Hunter Rouse (1906-1996) e logo depois foi modificado por Lewis F. Moody (1880-1953) da maneira como é usado atualmente.

É usado para tubos circulares e não circulares, é suficiente para substituir o diâmetro hidráulico para estes.

Como é feito e como é usado?

Como explicado acima, o diagrama Moody é feito de vários dados experimentais, apresentados graficamente. Aqui estão as etapas para usá -lo:

- Calcule o número de Reynolds N_R Para determinar se o fluxo é laminar ou turbulento.

- Calcular a rugosidade relativa por equação e_r = E/D, onde e É a rugosidade absoluta do material e D é o diâmetro interno do tubo. Esses valores são obtidos por tabelas.

- Agora que está disponível e_r e N_R, projetar verticalmente até atingir a curva correspondente ao e_r obtido.

- Projetar horizontalmente e à esquerda para ler o valor de F.

Um exemplo visualizará facilmente como o diagrama é usado.

Pode servir a você: Fluoreto de cálcio (CAF2): estrutura, propriedades, usos

-Exemplo 1 resolvido 1

Determine o fator de atrito da água a 160º F fluindo a uma taxa de 22 pés/s em um duto feito de ferro forjado não revestido e diâmetro interno de 1 polegada.

Solução

Os dados necessários (são encontrados nas tabelas):

Viscosidade cinemática da água em 160 ºF: 4.38 x 10^-6 pé²/s

A rugosidade absoluta de ferro forjado não coberto: 1.5 x 10 ^-4 pés

Primeiro passo

O número de Reynolds é calculado, mas não antes de passar o diâmetro interno de 1 polegada aos pés:

1 polegada = 0.0833 pés

N_R = (22 x 0.0833)/ 4.38 x 10^-6= 4.18 x 10 ⁵

De acordo com os critérios mostrados antes de ser um fluxo turbulento, o diagrama Moody permite que o fator de atrito correspondente seja obtido, sem ter que usar a equação de Colleebrook.

Segundo passo

Você tem que encontrar relativa aspereza:

e_r = 1.5 x 10 -4 / 0.0833 = 0.0018

Terceiro passo

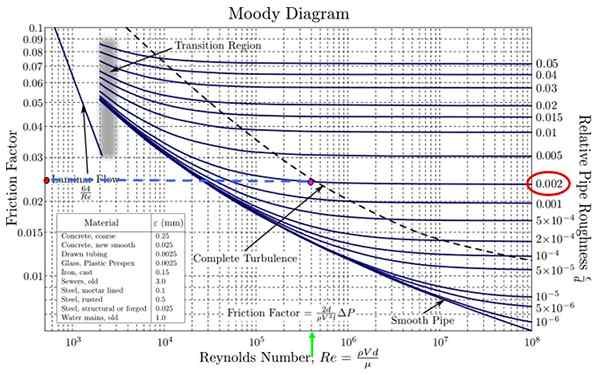
No diagrama sombrio fornecido, é necessário. Não há ninguém que corresponda exatamente em 0.0018, mas há um que se aproxima muito, o 0.002 (oval vermelho da figura).

Simultaneamente, o número de Reynolds correspondente é procurado no eixo horizontal. O valor mais semelhante ao 4.18 x 10 ⁵ é 4 x 10 ⁵ (seta verde na figura). A interseção de ambos é o ponto de Fuchsia.

Quarto passo

Projeto deixado para a linha pontilhada esquerda e chegue ao Orange Point. Agora estimar o valor de F, Levando em consideração que as divisões não têm o mesmo tamanho de uma escala logarítmica, tanto no eixo horizontal quanto no vertical.

O diagrama Moody fornecido na figura não tem divisões horizontais finas, portanto o valor de F em 0.024 (está entre 0.02 e 0.03, mas não é metade, mas um pouco menos).

Existem calculadoras on -line que usam a equação de Colleebrook. Um deles (ver referências) Fornecido Valor 0.023664639 para fator de atrito.

Formulários

O diagrama Moody pode ser aplicado para resolver três tipos de problemas, desde que sejam conhecidos o fluido e a rugosidade absoluta do tubo:

- Cálculo da queda de pressão ou a diferença nas pressões entre dois pontos, forneceu o comprimento do tubo, a diferença de altura entre os dois pontos a serem considerados, a velocidade e o diâmetro interno do tubo.

Pode atendê -lo: movimento pendular

- Determinação do fluxo, conhecido o comprimento e diâmetro do tubo, além da queda de pressão específica.

- Avaliação do diâmetro do tubo quando o comprimento, o fluxo e a queda de pressão entre os pontos a serem conhecidos são conhecidos.

Os problemas do primeiro tipo são resolvidos diretamente usando o diagrama, enquanto os do segundo e terceiro tipo exigem o uso de um pacote computacional. Por exemplo, naqueles do terceiro tipo, se o diâmetro do tubo não for conhecido, o número de Reynolds não poderá ser avaliado diretamente, nem a rugosidade relativa.

Uma maneira de resolvê -los é assumir um diâmetro interno inicial e a partir daí ajusta sucessivamente os valores para obter a queda de pressão especificada no problema.

-Exemplo 2 resolvido 2

Tem água a 160 ° F de fluxo estacionado ao longo de um tubo de 1 polegada em diâmetro de ferro forjado não coberto, a uma taxa de 22 pés/s. Determine a diferença de pressão causada pelo atrito e poder de bombeamento necessário para manter o fluxo em um trecho de tubo horizontal de L = 200 pés de comprimento.

Solução

Dados necessários: a aceleração da gravidade é de 32 pés/s² ; O peso específico da água a 160 ºf é γ = 61.0 lb força/pé³

Este é o tubo do exemplo resolvido 1, portanto o fator de atrito já é conhecido F, que foi estimado em 0.0024. Este valor é levado à equação de Darcy para avaliar as perdas de atrito:

O poder de bombeamento necessário é:

W = V. PARA. (p₁ - p₂)

Onde a é a seção transversal do tubo: a = p. (D²/4) = P. (0.0833²/4) Pé² = 0.00545 pés²

W = 22 pés /s . 2659.6 lb força / pé². 0.00545 pés²= 318.9 LB-Force . pés

O poder é melhor expresso em watts, para o qual o fator de conversão é necessário:

1 watt = 0.737 lb-force . pés

Portanto, o poder necessário para manter o fluxo é w = 432.7 w

Referências

1. Cimbala, c. 2006. Mecânica de fluidos, fundamentos e aplicações. Mc. Graw Hill. 335-342.
2. Franzini, J. 1999. A mecânica de fluidos com aplicação está em engenharia. Mc. Graw Hill.176-177.
3. Engenharia de LMNO. Fator de calculadora de fricção Moody. Recuperado de: lmnoeng.com.
4. Mott, r.  2006. Mecânica de fluidos. 4º. Edição. Pearson Education. 240-242.
5. A caixa de ferramentas de engenharia. Diagrama Moody. Recuperado de: EngineeringToolbox.com
6. Wikipedia. Gráfico Moody. Recuperado de: em.Wikipedia.org