Propriedades de derivados parciais, cálculo, exercícios

As derivados parciais de uma função com várias variáveis ​​independentes são aquelas que são alcançadas tomando o derivado comum em uma das variáveis, enquanto os outros são mantidos ou tomados como constantes.

O derivado parcial em uma das variáveis ​​determina como a função varia em cada ponto, por unidade de mudança a variável em questão. 

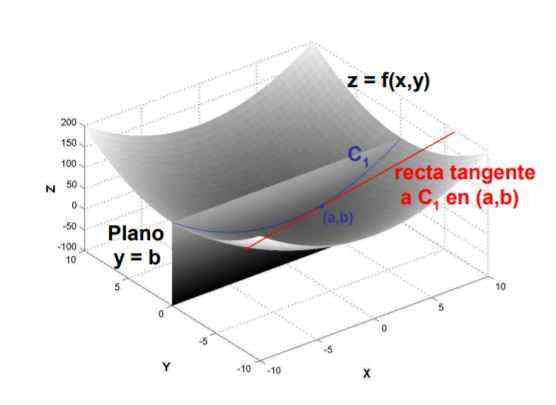figura 1. A inclinação da linha tangente à curva formada pela interseção do plano y = b com a superfície f (x, y) no ponto (a, b) é o derivado parcial de f em relação a x, avaliado nesse ponto. Fonte: UPM.é

Devido à sua definição, o derivado parcial é calculado, levando o limite matemático do quociente entre a variação da função e a variação da variável em relação ao que é derivado, quando a mudança do último tende a zero.

Suponha que o caso de uma função F Depende das variáveis x e e, isto é, para cada par (X, y) A é atribuído z: 

F: (x, y) → Z .

O derivado parcial da função z = f (x, y), em relação à x é definido como:

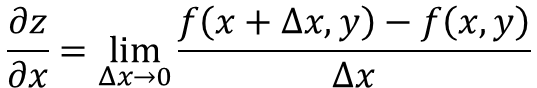
Agora, existem várias maneiras de denotar o derivado parcial de uma função, por exemplo:

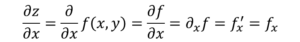
A diferença com a derivada comum, em termos de notação, é que o d de derivação é alterada para o símbolo ∂, conhecido como "jacobi d".

[TOC]

Propriedades de derivados parciais

O derivado parcial de uma função de várias variáveis, em relação a uma delas, é o derivado comum na referida variável e considerando o restante como fixo ou constante. Para encontrar o derivado parcial, as regras de derivação dos derivadas comuns podem ser usadas.

Abaixo das propriedades principais:

Pode atendê -lo: fator comum para agrupar termos: exemplos, exercícios

Continuidade

Se uma função f (x, y) tem derivados parciais em x e e no ponto (Xo, eu) então pode -se dizer que a função é contínua nesse ponto.

Regra da cadeia

Uma função f (x, y) Com derivados parciais contínuos em x e e, que por sua vez depende de um parâmetro t através de x = x (t) e y = y (t), Tem derivado comum em relação à variável t, que é calculado pela regra da cadeia:

d_t Z = ∂_xz d_tx + ∂_ez d_te

Propriedade de fechamento ou bloqueio

O derivado parcial em relação a uma das variáveis ​​de uma função F de duas ou mais variáveis (X, y, ...), É outra função g Nessas mesmas variáveis, por exemplo: 

G (x, y, ...) = ∂_e f (x, y, ...)

Isto é, a derivação parcial é uma operação que vai de Rⁿ a rⁿ. Nesse sentido, diz -se que é um operação fechada.

Derivados parciais sucessivos

Os sucessivos derivados parciais de uma função de várias variáveis ​​podem ser definidos, dando origem a novas funções nas mesmas variáveis ​​independentes.

Seja a função f (x, y). Os seguintes derivados sucessivos podem ser definidos:

F_Xx = ∂_xF ;  F_AA = ∂_AAF ; F_XY = ∂_XYF e F_Yx = ∂_YxF

Os dois últimos são conhecidos como Derivados mistos Porque eles envolvem duas variáveis ​​independentes diferentes.

Teorema de Schwarz

Ser uma função f (x, y), definido de tal maneira que seus derivados parciais são funções contínuas em um subconjunto aberto de R².

Então, para cada pares (X, y) Que eles pertencem ao referido subconjunto, os derivados mistos são idênticos:

∂_XYF = ∂_YxF

A declaração anterior é conhecida como Teorema de Schwarz.

Como os derivados parciais são calculados?

Derivados parciais são calculados semelhantes aos derivados de funções comuns em uma única variável independente. Quando o derivado parcial de uma função de várias variáveis ​​é tomado em relação a um deles, as outras variáveis ​​são tomadas como constantes.

Pode atendê -lo: metade dos 15

Abaixo estão vários exemplos:

Exemplo 1

Seja a função:

f (x, y) = -3x² + 2 (e - 3)²

É solicitado para calcular o primeiro derivado parcial em relação a x e o primeiro derivado parcial em relação a e.

Procedimento

Para calcular o parcial F em relação à x, toma e como constante:

∂_xF = ∂_x(-3x² + 2 (e - 3)² ) = ∂_x(-3x² )+ ∂_x(2 (e - 3)² ) = -3 ∂_x(x²) + 0 = -6x.

E por sua vez, para calcular o derivado em relação a e toma x como constante:

∂_eF = ∂_e(-3x² + 2 (e - 3)² ) = ∂_e(-3x² )+ ∂_e(2 (e - 3)² ) = 0 + 2 · 2 (y - 3) = 4y - 12.

Exemplo 2

Determine derivados parciais de segunda ordem:  ∂_Xxf, ∂_AAf, ∂_YxF e ∂_XYF Para a mesma função F do exemplo 1.

Procedimento

Nesse caso, como o primeiro derivado parcial já é calculado em x e e (Veja o Exemplo 1):

∂_XxF = ∂_x(∂_xf) = ∂_x(-6x) = -6

∂_AAF = ∂_e(∂_ef) = ∂_e(4y - 12) = 4

∂_YxF = ∂_e(∂_xf) = ∂_e(-6x) = 0

∂_XYF = ∂_x(∂_ef) = ∂_x(4y - 12) = 0

Observa -se que ∂_YxF = ∂_XYF, Assim, cumprindo o teorema de Schwarz, já que a função F e seus derivados parciais de primeira ordem são todas funções contínuas em R².

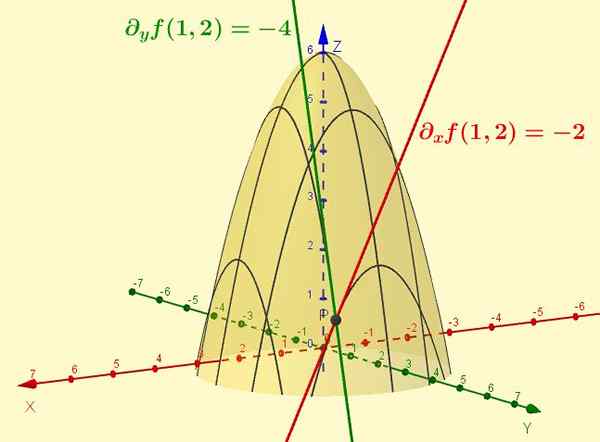
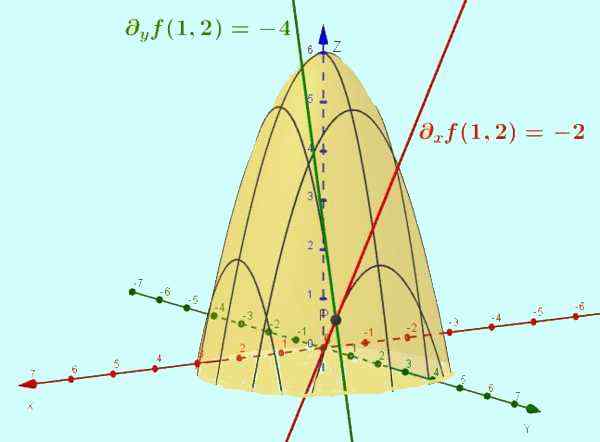Figura 2. A função z = f (x, y) = -x2 - y2 + 6 é a superfície mostrada na figura. O derivado parcial em relação a X é a inclinação da linha tangente da curva que resulta da interseção da referida superfície com o plano y = ctte (o caso específico é mostrado y = 2). Da mesma forma, a parte de f em relação e é a inclinação da tangente à interseção com x = 1, no ponto (1, 2, 1).

Exercícios resolvidos

Exercício 1

Seja a função:

Pode servir a você: sucessões quadráticas: exemplos, regra e exercícios resolvidos

f (x, y) = -x² - e² + 6

Encontre funções G (x, y) = ∂_xF  e H (x, y) = ∂_eF.

Solução

O derivado parcial de F em relação à x, para o qual a variável e Torna -se constante:

G (x, y) = - 2x

Da mesma forma, o derivado parcial de g em relação à e, fazendo x constante, resultando na função h:

H (x, y) = -2y

Exercício 2 

Avalie o ponto (1, 2) As funções f (x, y) e G (x, y) do Exercício 1. Interpretar os resultados.

Solução

Os valores são substituídos x = 1 e y = 2 obtenção:

F (1,2) = -(1)² -(2)² + 6 = -5 + 6 = 1

Este é o valor que leva a função f quando avaliado nesse ponto.

A função f (x, y) É uma superfície bidimensional e coordenada z = f (x, y) É a altura da função para cada par (X, y). Quando o par é levado (1.2), A altura da superfície f (x, y) é Z = 1.

A função G (x, y) = - 2x representa um avião no espaço tridimensional cuja equação é Z = -2x o bem -2x + 0 e -z = 0.

O referido avião é perpendicular ao plano Xz E passar pelo ponto (0, 0, 0). Quando avaliado em x = 1 e y = 2 então Z = -2. Observe que o valor z = g (x, y) É independente do valor atribuído à variável e.

Por outro lado, se a superfície cruzar f (x, y) Com o avião y = c, com c constante, você tem uma curva no avião Zx: z = -x² - c² + 6.

Neste caso o derivado de z em relação à x coincide com o derivado parcial de f (x, y) em relação à x: d_x Z = ∂_xF .

Ao avaliar no par (x = 1, y = 2) O derivado parcial nesse ponto ∂_xF (1.2) É interpretado como a inclinação da linha tangente à curva z = -x² + 2 no ponto (x = 1, y = 2) E o valor desta inclinação é -2.

Referências

1. Ayres, f. 2000. Cálculo. 5ed. Mc Graw Hill.
2. Derivados parciais de uma função em várias variáveis. Recuperado de: construção.Upm.é.
3. Leithold, l. 1992. Cálculo com geometria analítica. Harla, s.PARA.
4. Purcell, e. J., Varberg, d., & Rigdon, S. E. (2007). Cálculo. México: Pearson Education.
5. Gorostizaga J. C. Derivados parciais. Recuperado de: ehu.EUS
6. Wikipedia. Derivativo parcial. Recuperado de: é.Wikipedia.com.