Derivados implícitos como são resolvidos e resolvidos exercícios

As derivados implícitos São ferramentas usadas em uma técnica de diferenciação aplicada às funções. Eles se aplicam quando não é possível, sob métodos regulares, realizam a liberação da variável dependente que deve derivar. Esta autorização é feita com base na variável independente.

Por exemplo, na expressão 3xy³ - 2y + xy² = xy, você não pode obter a expressão que define "y", dependendo de "x". Para que quando a expressão diferencial dy/dx pode ser obtida.

[TOC]

Como os derivados implícitos são resolvidos?

Para resolver uma implicação, é baseado em uma expressão implícita. Por exemplo: 3xy³ - 2y + xy² - Xy = 0. Isso já foi claramente limpo, no entanto, para isso, não é uma condição necessária para obter o derivado de y em relação a x. Em seguida, cada um dos elementos é derivado respeitando a regra da cadeia para funções mistas:

3xy³ Consiste em 2 variáveis, portanto d (3xy³) Será tratado como o derivado de um produto de funções.

D (3xy³)/dx = 3y³ + 3y².(3x) e '= 3y³ + 9xy² e'

Onde o elemento e 'é conhecido como "e primo”E dy/dx representa

-2y deriva de acordo com a lei k.U = k.OU'

D (-2y) = -2 e '

XY² supõe outro diferencial composto por um produto de funções

D (XY²) = y² + 2xy e '

-XY é uma maneira homóloga

d (-xy) = -y -x e '

Eles são substituídos em igualdade, sabendo que o derivado zero é zero.

3y³ + 9xy² e ' - 2 e' + e² + 2xy e ' - y - x e' = 0

Os elementos que têm o termo e 'são agrupados em um lado da igualdade

Pode atendê -lo: vetores colineais

3y³ + e² - y = -9xy² e ' + 2 e' + x e '

O fator comum e 'no membro certo da igualdade é extraído

3y³ + e² - y = y '(-9xy² + x + 2)

Finalmente, o termo que multiplica e '. Obtendo assim a expressão correspondente ao derivado implícito de y em relação a x.

e '= dy/dx = (3y³ + e² - y)/(-9xy² + x + 2)

Regra da cadeia

Na derivação implícita, a regra da cadeia é sempre respeitada. Todas as expressões diferenciais serão dadas dependendo da variável independente x. Para que qualquer variável θ diferente de x deve incluir o termo dθ/dx após ser derivado.

Este termo aparecerá apenas no primeiro grau ou com expoente igual a 1. Esta qualidade deixa completamente claro nos métodos de fatoração tradicional. Para que seja possível obter a expressão que define o diferencial dθ/dx.

Na regra da cadeia, a natureza progressiva da diferenciação ou processo de derivada é mostrado. Onde para qualquer função composta f [g (x)], a expressão diferencial de f terá que ser

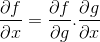
Ordem operacional

Em cada lei de fórmula ou derivação aplicada, a ordem das variáveis ​​deve ser levada em consideração. Os critérios associados à variável independente são respeitados, sem alterar sua correlação com a variável dependente.

A proporção da variável dependente no momento da derivada é tomada diretamente.; Com a exceção de que isso será considerado como uma segunda função, e é por isso que os critérios da regra da cadeia para funções mistas são aplicadas.

Isso pode ser desenvolvido em expressões com mais de 2 variáveis. Sob os mesmos princípios, todos os diferenciais referentes a variáveis ​​dependentes serão denotados.

Pode atendê -lo: qual é a diretriz? (Geometria)

Graficamente o mesmo critério é tratado que define o derivado. Embora a derivada seja a inclinação da linha tangente à curva no plano, o restante dos diferenciais pertencentes às variáveis ​​dependentes (dy/dx, dz/dx) representam planos tangentes aos corpos vetoriais descritos pelas funções de múltiplas variáveis.

Implícito de uma função

Dizem que uma função é implicitamente definida, se a expressão y = f (x) puder ser representada como uma função variável múltipla f (x, y) = 0 enquanto f é definida no plano r².

3xy³ - 2y + xy² = x e pode ser escrito na forma 3xy³ - 2y + xy² - Xy = 0

Em vista da impossibilidade de explicar a função y = f (x).

História

O cálculo diferencial começou a ser nomeado por vários pesquisadores matemáticos, por volta do século XVII. A primeira vez que foi mencionada foi através das contribuições de Newton e Leibniz. Ambos trataram o cálculo diferencial de diferentes pontos de vista, mas convergindo em seus resultados.

Enquanto Newton se concentrou na diferenciação como uma taxa de velocidade ou variação, a abordagem de Leibniz era mais geométrica. Pode -se dizer que Newton atacou as conjecturas deixadas por Apollonius de Perge e Leibniz, as idéias geométricas de Fermat.

A derivação implícita aparece imediatamente quando as equações diferenciais e abrangentes consideram. Eles estenderam o conceito geométrico de Leibniz para R³ e até espaços multidimensionais.

Formulários

Derivados implícitos são usados ​​em várias situações. Eles são comuns em problemas de taxa de câmbio entre variáveis ​​relacionadas, onde, dependendo do senso de estudo, as variáveis ​​serão consideradas dependentes ou independentes.

Eles também têm aplicações geométricas interessantes, como em problemas de reflexões ou sombras, em figuras cuja forma pode ser modelada matematicamente.

Pode servir a você: amostragem de cotas: método, vantagens, desvantagens, exemplos

Eles são de uso frequente nas áreas de economia e engenharia, bem como em várias investigações de fenômenos naturais e edifícios experimentais.

Exercícios resolvidos

Exercício 1

Defina a expressão implícita que define DY/DX

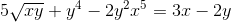
Cada elemento é diferente da expressão

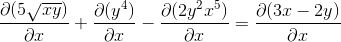
Estabelecendo a regra da cadeia em cada caso competente

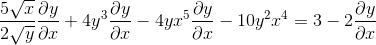
Agrupando em um lado da igualdade os elementos que têm dy/dx

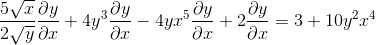
Está considerando usando o fator comum

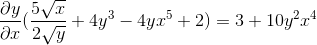
É limpo pela obtenção da expressão procurada

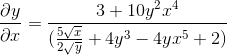
Exercício 2

Defina a expressão implícita que define DY/DX

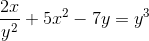
Expressando os derivados a realizar

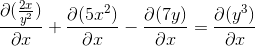
Derivando implicitamente de acordo com a regra da cadeia

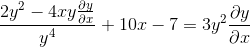
Factorizando elementos comuns

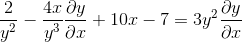
Agrupando o termo dy/dx em um lado da igualdade

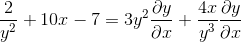
Fator comum para elemento diferencial

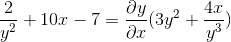
Limparemos e obtemos a expressão procurada

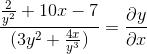
Referências

1. Cálculo de uma única variável. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 de novembro. 2008
2. O teorema da função implícita: história, teoria e aplicações. Steven G. Krantz, Harold R. Parques. Springer Science & Business Media, 9 de novembro. 2012
3. Análise multivariável. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 de dezembro. 2010
4. Dinâmica do sistema: modelagem, simulação e controle de sistemas mecatrônicos. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 de março. 2012
5. Cálculo: Matemática e Modelagem. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 de janeiro. 1999