Derivado do cálculo cotangente, demonstração, exercícios

O Derivado de cotangent É igual ao oposto do quadrado da colheita “-CSC²". Esta fórmula é devida a leis derivadas por definição e à diferenciação de funções trigonométricas. É indicado da seguinte maneira:

D (ctg u) = -csc² ou . du

Onde "du" simboliza a expressão derivada da função de argumento, em relação à variável independente.

Fonte: Pixabay.com

[TOC]

Como é calculado?

O procedimento para o desenvolvimento desses derivados é bastante simples. Apenas identificar o argumento e o tipo de função que ele representa.

Por exemplo, a expressão CTG (F/G) apresenta uma divisão em seu argumento. Isso precisará de uma diferenciação em relação a u/v, depois de desenvolver o zip.

Cotangent é a função recíproca da tangente. Algebraicamente isso significa que:

(1/tg x) = ctg x

Ctg x = cos x / sen x

É incorreto dizer que a função cotangente é o "inverso" da tangente. Isso ocorre porque a função inversa da tangente por definição é arco tangente.

(TG^-1 x) = arctg x

De acordo com a trigonometria pitagórica, o cotangente está envolvido nas seções a seguir:

Ctg x = (cos x) / (sin x)

Ctg² X + 1 = CSC² x

De acordo com a trigonometria analítica, responde às seguintes identidades:

Ctg (a + b) = (1 - tg a . Tg b) / (tg a + tg b)

Ctg (a - b) = (1 + tg a . Tg b) / (tg a - tg b)

CTG (2A) = (1 - TG² a) / (2tg a)

Características da função cotangente

É necessário analisar várias características da função f (x) = ctg x para poder definir os aspectos necessários para estudar sua diferença e aplicação.

Assíntotas verticais

A função cotangente não é definida nos valores que fazem a expressão "senx" zero. Devido ao seu CTG equivalente x = (cos x) / (sin x), ele terá uma indeterminação em todo o "nπ" com N pertencente aos números inteiros.

Pode atendê -lo: geometria analítica

Isto é, em cada um desses valores de x = nπ, haverá uma assíntota vertical. À medida que o valor das se aproxima de cotangente e, ao se aproximar da direita, a função aumentará indefinidamente.

Domínio

O domínio da função cotangente é expresso pelo conjunto x ∈ R / x ≠ nπ, n ∈ Z. Isso é lido como "X que pertence ao conjunto de números reais de modo que X é diferente de Nπ, com N pertencente a todo o número de números".

Faixa

A classificação da função cotangente abrange de menos para mais infinito. É por isso que pode -se concluir que sua classificação é o conjunto de números N Reais.

Frequência

A função cotangente é periódica e seu período é igual a π. Dessa maneira.

Comportamento

É uma função ímpar, já que CTG (-x) = - ctg x. Dessa maneira, sabe -se que a função apresenta uma simetria em relação à origem coordenada. Ele também apresenta uma diminuição em cada intervalo localizado entre 2 assíntotas verticais sucessivas.

Não possui valores máximos ou mínimos, porque suas abordagens para assíntotas verticais têm comportamentos onde a função cresce ou diminui indefinidamente.

Os zeros ou raízes da função cotangente são encontrados nos múltiplos ímpares de π/2. Isso significa que CTG x = 0 é cumprido nos valores da forma x = nπ/2 com uma totalidade.

Demonstração

Existem 2 maneiras de demonstrar o derivado da função cotangente.

Demonstração diferencial trigonométrica

A derivada da função cotangente é demonstrada a partir de seu equivalente em seios e cosenos.

Pode servir a você: Álgebra Booleana: História, Teoremas e Postulados, Exemplos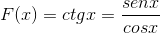

É sobre o derivado de uma divisão de funções

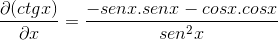
Depois de derivar, os fatores são agrupados e as identidades pitagóricas são procuradas para imitar

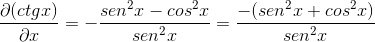
Substituindo identidades e aplicação de reciprocidade, a expressão é obtida

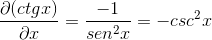
Definição de definição derivada

A seguinte expressão corresponde à derivada por definição. Onde a distância entre 2 pontos da função está se aproximando de zero.

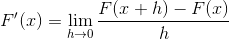
Substituindo para o cotangente que você precisa:

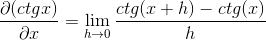
Identidades se aplicam à soma dos argumentos e reciprocidade

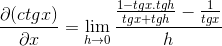
A fração do numerador é operada tradicionalmente

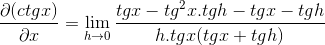
Eliminando elementos opostos e o fator comum de desenho é obtido

Aplicando identidades pitagóricas e reciprocidade

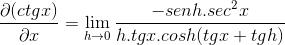
Os elementos avaliados em x são constantes em relação ao limite, portanto podem deixar o argumento disso. Então os limites trigonométricos são aplicados.

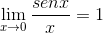
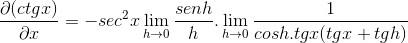
O limite é avaliado

Então está considerando até atingir o valor desejado

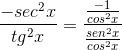
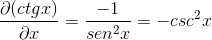
Isso é demonstrado pelo derivado de cotangente como o oposto do quadrado da colheita.

Exercícios resolvidos

Exercício 1

De acordo com a função F (x), defina a expressão F '(x)

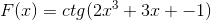
A derivação correspondente é aplicada em relação à regra da cadeia

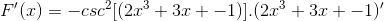
Derivando o argumento

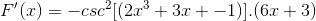
Às vezes é necessário aplicar identidades recíprocas ou trigonométricas para adaptar as soluções.

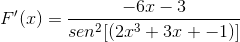
Exercício 2

Defina a expressão diferencial correspondente a f (x)

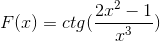
De acordo com a fórmula de derivação e respeitando a regra da cadeia

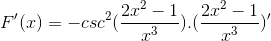
O argumento é derivado, enquanto o resto permanece o mesmo

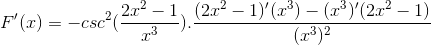
Derivando todos os elementos

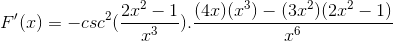
Operando de uma maneira tradicional os produtos da mesma base

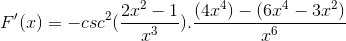
Os mesmos elementos são adicionados e o fator comum é extraído

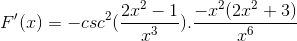
Os sinais são simplificados e operados. Dando lugar à expressão completamente derivada

Pode atendê -lo: diferença entre uma fração comum e um número decimal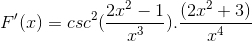

Referências

1. Série trigonométrica, volume 1. PARA. Zygmund. Cambridge University Press, 2002
2. Cálculo de uma única variável. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 de novembro. 2008
3. Cálculo com trigonometria e geometria analítica. John h. Saxon, John Saxon, Frank Wang, Diana Harvey. Saxon Publishers, 1988
4. Análise multivariável. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 de dezembro. 2010
5. Dinâmica do sistema: modelagem, simulação e controle de sistemas mecatrônicos. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 de março. 2012
6. Cálculo: Matemática e Modelagem. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 de janeiro. 1999