Decodificação de expressões
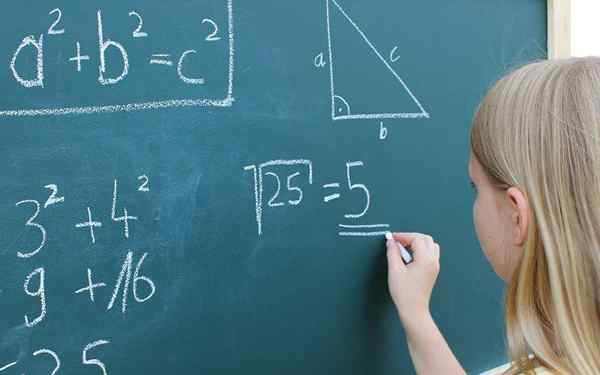
- 4194
- 314
- Tim Mann
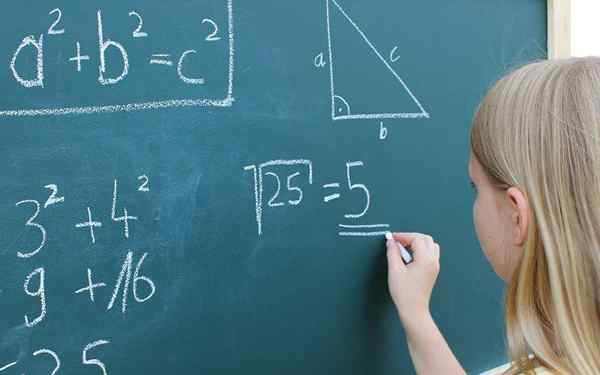 Expressões matemáticas. Com licença
Expressões matemáticas. Com licença Qual é a decodificação de expressões?
O Decodificação de expressões Refere -se à maneira de expressar verbalmente uma expressão matemática. Em matemática, um expressão, Também chamado de expressão matemática, é uma combinação de coeficientes literais e partes literais através de outros sinais matemáticos (+, -, x, ±, /, [],), a fim de formar uma operação matemática.
Em palavras mais simples, os coeficientes são representados por números, enquanto a parte literal é composta de letras (as três primeiras letras do alfabeto, a, b e c, são geralmente usadas para designar a parte literal).
Por sua vez, essas "letras" representam magnitudes, variáveis e constantes às quais um valor numérico pode ser atribuído.
Expressões matemáticas consistem em termos, que são cada um dos elementos que são separados por símbolos de operações. Por exemplo, a seguinte expressão matemática tem quatro termos:
5x2 + 10x + 2x + 4
Deve -se notar que as expressões podem ser constituídas apenas por coeficientes, por coeficientes e partes literais e somente por partes literais.
Por exemplo:
25 + 12
2x + 2y (expressão algébrica)
3x + 4/y + 3 (expressão algébrica irracional)
x + y (expressão algébrica inteira)
4x + 2y2 (Expressão algébrica inteira)
Decodificação de expressões matemáticas
Decodificação de expressões matemáticas simples
1. A + b: a soma de dois números
Por exemplo: 2 + 2: a soma de dois e dois
2. A + b + c: a soma de três números
Por exemplo: 1 + 2 + 3: a soma de um, dois e três
3. A - b: a subtração (ou a diferença) de dois números
Por exemplo: 2 - 2: a subtração (ou diferença) de dois e dois
4. A x b: o produto de dois números
Pode atendê -lo: abordagem problemáticaPor exemplo: 2 x 2: o produto de dois e dois
5. para ÷ B: A proporção de dois números
Por exemplo: 2/2: o quociente de dois e dois
6. 2 (x): duas vezes um número
Por exemplo: 2 (23): duas vezes 23
7. 3 (x): triplo de um número
Por exemplo: 3 (23): o triplo de 23
8. 2 (a + b): duas vezes a soma de dois números
Por exemplo: 2 (5 + 3): duas vezes a soma de cinco e três
9. 3 (A + B + C): Triple da soma de três números
Por exemplo: 3 (1 + 2 + 3): Triple da soma de um, dois e três
10. 2 (a - b): duas vezes a diferença de dois números
Por exemplo: 2 (1 - 2): duas vezes a diferença de um e dois
onze. x/2: metade de um número
Por exemplo: 4/2: metade de quatro
12. 2n + x: a soma de um número duplo e outro número
Por exemplo: 2 (3) + 5: a soma de três e cinco
13. X> y: "Equis" é maior que "Ye"
Por exemplo: 3> 1: três é maior que um
14. x < y: “Equis” es menor que “ye”
Por exemplo: 1 < 3: Uno es menor que tres
quinze. X = y: "Equis" é igual a "ye"
Por exemplo: 2 x 2 = 4: o produto de dois e dois é igual a quatro
16. x2 : O quadrado de um número ou um número quadrado
Por exemplo: 52 : Os cinco ou cinco quadrados quadrados
17. x3: O cubo de um número ou um número no cubo
Por exemplo: 53: Os cinco ou cinco cubos para o cubo
Pode atendê -lo: método qualitativo18. (A + b)2: O quadrado da soma de dois números
Por exemplo: (1 + 2)2: O quadrado da soma de um e dois
19. (x - y)/2: metade da diferença de dois números
Por exemplo: (2 - 5)/2: metade da diferença de dois e cinco
vinte. 3 (x + y)2: Triple do quadrado da soma de dois números
Por exemplo: 3 (2 + 5)2 : O triplo do quadrado da soma de dois e cinco
vinte e um. (A + b)/2: dois números
Por exemplo: (2 + 5)/2: os dois e cinco semi -sísmicos
Decodificação de expressões algébricas
1. 2 x5 + 7/y + 9: [dois equis aumentados para cinco] mais [sete sobre você] mais [nove]
2. 9 x + 7y + 3 x6 - 8 x3 + 4 y: [nove equis] mais [sete anos] mais [três equis levantados para seis] menos [oito equis aumentados para 3] mais [quatro anos]
3. 2x + 2y: [dois equis] mais [dois anos]
4. X/2 - y5 + 4y5 + 2x2: [x em 2] menos [e aumentado para cinco] mais [quatro e aumentados para cinco] mais [dois quadrados levantados]
5. 5/2 x + y2 + X: [cinco em dois equis] mais [e quadrado] mais [Equis]
Decodificação polinomial
1. 2x4 + 3x3 + 5x2 + 8x + 3: [dois de Equis levantados para os quatro] mais [três de Equis elevados a três mais] mais [cinco dos quadrados elevados] mais [8 de Equis] mais três
2. 13 e6 + 7y4 + 9y3 + 5y: [treze de e elevado a mais] mais [sete e elevado para os quatro mais] [nove e elevados para os três] mais [cinco de vocês]]
3. 12z8 - 5z6 + 7z5 + z4 - 4z3 + 3z2 + 9z: [doze de Zeta elevados a oito] menos [cinco de Zeta elevaram a mais seis] [sete de Zeta elevaram a cinco] mais [Zeta elevados a quatro] menos [quatro de Zeta elevados ao cubo] mais [três de Zeta elevado ao quadrado] mais [nove de Zeta]
Pode servir a você: importância da matemática para abordar situações físicasReferências
- Expressões com variáveis com variáveis. Recuperado de Khanacademy.org.
- Compreensão de expressões algébricas por usuários experientes de matemática. NCBI se recuperou.Nlm.NIH.Gov.
- Escrevendo expressões matemáticas. Recuperado de Mathgoodies.com.

