Dados não agrupados exemplos e exercícios resolvidos

O Dados não agrupados Eles são aqueles que, obtidos de um estudo, ainda não estão organizados por classes. Quando é um número gerenciável de dados, geralmente 20 ou menos, e existem poucos dados diferentes, eles podem ser tratados como não agrupados e extrair informações valiosas deles.

Os dados não agrupados vêm como é da pesquisa ou do estudo realizado para obtê -los e, portanto, não possuem processamento. Vejamos alguns exemplos:

figura 1. Os dados não agrupados são diretamente de qualquer estudo e não foram classificados. Fonte: pxhere.

-Resultados de um exame de IC de coeficiente intelectual em 20 estudantes aleatórios de uma universidade. Os dados obtidos foram os seguintes:

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112.106

-Idades de 20 funcionários de uma cafeteria muito popular:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20, 20

-As notas finais médias de 10 alunos de uma aula de matemática:

3.2; 3.1; 2,4; 4.0; 3.5; 3.0; 3.5; 3.8; 4.2; 4.9

[TOC]

Propriedades de dados

Existem três propriedades importantes que caracterizam um conjunto de dados estatísticos são agrupados ou não, que são:

-Posição, qual é a tendência dos dados a serem agrupados em torno de certos valores.

-Dispersão, Um indicativo de quão dispersados ​​ou disseminados são os dados em torno de um determinado valor.

-Forma, Refere -se à maneira como os dados são distribuídos, o que pode ser visto quando um gráfico deles é construído. Existem curvas muito simétricas e também tendenciosas, à esquerda ou à direita de um certo valor central.

Para cada uma dessas propriedades, existem várias medidas que as descrevem. Uma vez obtidos, eles nos dão um panorama de comportamento de dados:

-As medidas de posição mais usadas são uma média aritmética ou simplesmente médias, mediana e moda.

-Na dispersão, o intervalo, a variação e o desvio padrão são usados ​​com frequência, mas eles não são as únicas medidas de dispersão.

Pode atendê -lo: homotecia

-E para determinar a forma, a média e a mediana são comparadas através do viés, como será visto em breve.

Cálculo da média, mediana e moda

-A média aritmética, Também conhecido como média e indicado como x, é calculado da seguinte forma:

X = (x₁ + x₂ + x₃ +... x_n) / n

Onde x₁, x₂,.. . x_n, são os dados e n é o total deles. Em somação da soma, existe:

Aqui, o índice eu representa os dados 1, dados 2, dados 3 e assim por diante, até chegar ao único, que é o último.

-A mediana É o valor que aparece no meio de uma sucessão ordenada de dados; portanto, para obtê -los, é necessário ordenar os dados primeiro.

Se o número de observações for estranho, não há problema em encontrar o ponto médio do conjunto, mas se tivermos um par de dados, os dois dados centrais serão procurados e calculados.

-Moda É o valor mais comum observado no conjunto de dados. Nem sempre existe, pois é possível que nenhum valor seja repetido com mais frequência do que outro. Também pode haver dois dados com igual frequência; nesse caso, se fala de uma distribuição bi-modal.

Ao contrário das duas medidas anteriores, a moda pode ser usada com dados qualitativos.

Vamos ver como essas medidas de posição são calculadas com um exemplo:

Exemplo resolvido

Suponha que você queira determinar a média aritmética, a mediana e a moda no exemplo proposto no início: as idades de 20 funcionários de uma cafeteria:

24, 20, 22, 19, 18, 27, 25, 19, 27, 18, 21, 22, 23, 19, 22, 27, 29, 23, 20, 20

O metade É calculado simplesmente adicionando todos os valores e dividindo por n = 20, que é o número total de dados. Desta maneira:

Pode atendê -lo: relações de proporcionalidade: conceito, exemplos e exercícios

X = (24 + 20 + 22 + 19 + 18 + 27+ 25 + 19 + 27 + 18 + 21 + 22 + 23 + 21+ 19 + 22 + 27+ 29 + 23+ 20) / 20 =

= 22.3 anos.

Para encontrar o mediana É necessário solicitar o conjunto de dados primeiro:

18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 22, 23, 23, 24, 25, 27, 27, 27, 29

Como são alguns dados, os dois dados centrais, destacados em negrito, são tomados e médios. Porque ambos têm 22 anos, a mediana é de 22 anos.

finalmente, o moda É o fato que é mais repetido ou que cuja frequência é maior, sendo esses 22 anos.

Alcance, variação, desvio padrão e viés

O intervalo é simplesmente a diferença entre o major e o menor dos dados e permite que sua variabilidade aprecie rapidamente. Mas, além, existem outras medidas de dispersão que oferecem mais informações sobre a distribuição de dados.

Variação e desvio padrão

A variação é indicada como S e é calculada pela expressão:

É frequentemente trabalhado com a quase-fio em vez da variação, que é calculada da mesma maneira, dividida apenas por N-1, em vez de fazer entre n:

Como a variação é a soma dos quadrados, resulta no quadrado da unidade de amostra. Por exemplo, no estudo das idades dos funcionários da cafeteria, a variação ocorreria em anos².

Então, para interpretar corretamente os resultados, o desvio padrão como a raiz quadrada da variação, ou também a quase-desvio padrão, é definida, que é a raiz quadrada da quase-natalidade:

Viés

É a comparação entre o x médio e o mediano med:

-Sim med = mídia x: os dados são simétricos.

-Quando x> med: tendenciosos para a direita.

-E se x < Med: los datos sesgan hacia la izquierda.

Exercício resolvido

Encontre média, mediana, moda, classificação, variação, desvio padrão e viés para os resultados de um exame de coeficiente intelectual de 20 estudantes de uma universidade:

Pode atendê -lo: funções matemáticas

119, 109, 124, 119, 106, 112, 112, 112, 112, 109, 112, 124, 109, 109, 109, 106, 124, 112, 112, 106

Solução

Pediremos os dados, pois será necessário encontrar a mediana.

106, 106, 106, 109, 109, 109, 109, 109, 112, 112, 112, 112, 112, 112, 119, 119, 124, 124, 124

E nós os colocaremos em uma mesa da seguinte maneira, para facilitar os cálculos. A segunda coluna intitulada "acumulada" é a soma dos dados correspondentes mais o anterior.

Esta coluna encontrará facilmente a média, dividindo o último acumulado entre o número total de dados, como visto no final da coluna "acumulada":

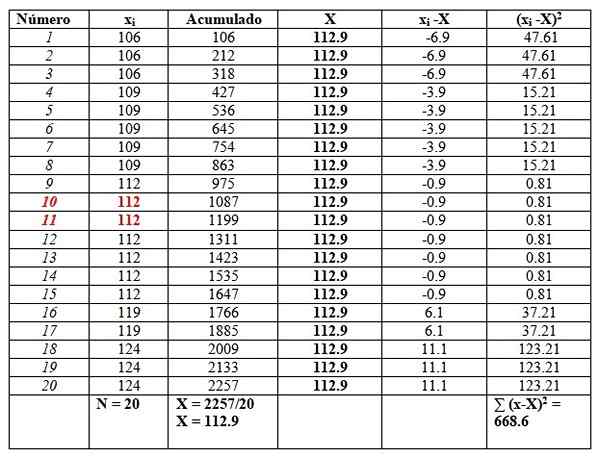
X = 112.9

A mediana é a média dos dados centrais destacados em vermelho: número 10 e número 11. Como são iguais, a mediana é 112.

Finalmente, a moda é o valor mais repetido e é 112, com 7 repetições.

Quanto às medidas de dispersão, o intervalo é:

124-106 = 18.

A variação é obtida dividindo o resultado final da coluna certa entre n:

S = 668.6/20 = 33.42

Nesse caso, o desvio padrão é a raiz quadrada da variação: √33.42 = 5.8.

Por outro lado, os valores da quaseza e do desvio padrão quase são:

s_c= 668.6/19 = 35.2

Quase-desvio padrão = √35.2 = 5.9

Finalmente, o viés é um pouco à direita, já que a média de 112.9 é maior que a mediana 112.

Referências

1. Berenson, m. 1985. Estatística para administração e economia. Inter -American S.PARA.
2. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
3. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
4. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
5. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.