Matemática

Definição de curtose, tipos, fórmulas, para que é, por exemplo,

Definição de curtose, tipos, fórmulas, para que é, por exemplo,

O Curtose ou curtose É um parâmetro estatístico que serve para caracterizar a distribuição de probabilidade de uma variável aleatória, indicando o grau de concentração de valores em torno da medida central. Isso também é conhecido como "grau de pico".

O termo vem do grego "Kurtos", que significa arqueado; portanto, a curtose indica o grau de apontamento ou achatamento da distribuição, como visto na figura a seguir:

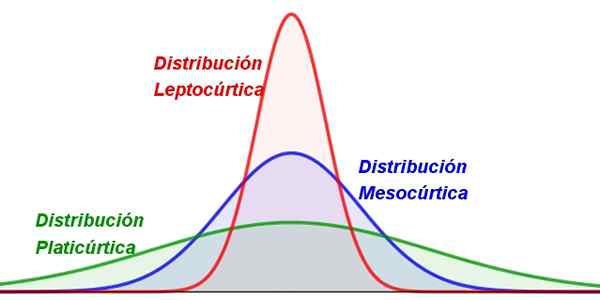figura 1. Diferentes tipos de curtose. Fonte: f. Zapata.

Quase todos os valores de uma variável aleatória tendem a agrupar em torno de um valor central, como a média. Mas em algumas distribuições, os valores são mais dispersos do que em outros, resultando em curvas mais achatadas ou mais delgadas.

[TOC]

Definição

A curtose é um valor numérico de cada distribuição de frequência, que de acordo com a concentração de valores em torno da média, é classificada em três grupos:

-Leptocúrico: em que os valores são muito agrupados em torno da média, portanto a distribuição é bastante pontiaguda e esbelta (Figura 1, à esquerda).

-Mesocúrico: Tem uma concentração moderada de valores em torno da média (Figura 1 no centro).

-Filicúrico: Esta distribuição tem uma forma mais ampla, porque os valores tendem a ser mais dispersos (Figura 1 à direita).

Fórmulas e equações

A curtose pode ter qualquer valor, sem limitações. Seu cálculo é realizado dependendo da maneira como os dados são entregues. A notação usada em cada caso é a seguinte:

-Coeficiente de cortose: g2

-Média aritmética: X ou x com barra

-Um I-EME: xYo

-O desvio padrão: σ

-O número de dados: N

-A frequência do i-esimo: FYo

-Marca de classe: mxYo

Com essa notação, apresentamos algumas das fórmulas mais usadas para encontrar curtose:

Pode servir a você: espaço vetorial: base e dimensão, axiomas, propriedades

- Curtose de acordo com a apresentação dos dados

Sem agrupamento ou dados agrupados em frequências

Dados agrupados em intervalos

Excesso de curtose

Tambem chamando Coeficiente apontador de Fisher qualquer Medida de Fisher, Serve para comparar a distribuição em estudo com a distribuição normal.

Quando o excesso de curtose vale 0, estamos na presença de uma distribuição normal ou de Gauss Bell. Dessa forma, desde que o excesso de bronzeamento de uma distribuição seja calculado, estamos realmente comparando -o com a distribuição normal.

Tanto para os dados sem agrupamento quanto para os dados agrupados, o coeficiente de apontar Fisher, indicado por K, é:

K = g2 - 3

No entanto, pode -se demonstrar que a curtose da distribuição normal é 3, portanto, se o coeficiente apontador do Fisher for 0 ou próximo a 0 e há uma distribuição mesocúrica. Se k> 0 a distribuição é leptoCuric e se k<0 es platicúrtica.

Para que é curtose para?

Curtose é uma medida de variabilidade usada para caracterizar a morfologia de uma distribuição. Dessa maneira, as distribuições simétricas podem ser comparadas com a mesma dispersão média e igual (dada pelo desvio padrão).

Ter medidas de variabilidade garante que as médias sejam confiáveis ​​e ajudem a controlar variações de distribuição. Como exemplo, vamos analisar essas duas situações.

3 Salários dos departamentos

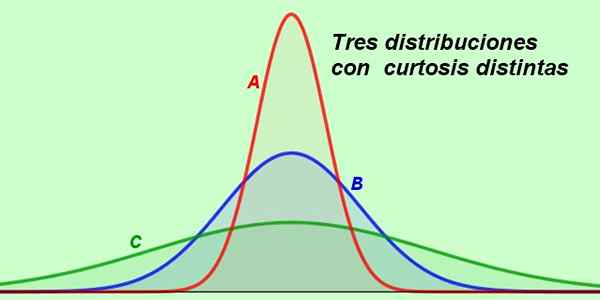
Suponha que o gráfico a seguir mostre as distribuições no salário de 3 departamentos da mesma empresa:

Figura 2. Três distribuições diferentes ilustram situações práticas. (Preparado por Fanny Zapata)

A curva A é a mais esbelta de todas e, na sua forma.

Pode atendê -lo: números inteiros

Por sua parte no Departamento B, a curva salarial segue uma distribuição normal, uma vez que a curva é mesocúrica, na qual assumimos que os salários foram distribuídos aleatoriamente.

E, finalmente, temos a curva C que é muito achatada, um sinal de que neste departamento a faixa salarial é muito mais ampla do que nos outros.

Os resultados de um exame

Suponha agora que as três curvas da Figura 2 representam os resultados de um exame aplicado a três grupos de estudantes do mesmo assunto.

O grupo cujas qualificações são representadas pela curva para leptocúrico, é bastante homogêneo, a maioria obteve uma classificação média ou fechada.

Também é possível que o resultado tenha sido devido ao fato de as perguntas do exame ter mais ou menos o mesmo grau de dificuldade.

Por outro lado, os resultados do Grupo C indicam maior heterogeneidade no grupo, que provavelmente contém estudantes comuns, alguns estudantes mais destacados e certamente outro menos atento.

Ou isso pode significar que as questões do teste tinham graus muito diferentes de dificuldade.

A curva B é mesocúrica, indicativa de que os resultados do teste seguiram uma distribuição normal. Este geralmente é o caso mais frequente.

Exemplo resolvido de curtose

Encontre o coeficiente apontador de Fisher para as seguintes notas, obtidas em um exame de física para um grupo de estudantes, com uma escala de 1 a 10:

5, 5, 4, 7, 7,7, 9, 8, 9, 4, 3

Solução

A expressão a seguir será usada para dados não agrupados, fornecidos nas seções anteriores:

Com o coeficiente de Fisher Point dado por:

Pode servir a você: identidades pitagóricas: demonstração, exemplo, exercícios

K = g2 - 3

Este valor permite saber o tipo de distribuição.

Para calcular g2 É conveniente fazê -lo de maneira ordenada, passo a passo, uma vez que várias operações aritméticas devem ser resolvidas.

Passo 1

Primeiro, a média das qualificações é calculada. Existem n = 11 dados.

X = (5+5+4+7+7+7+9+8+9+4+3)/11 = 6.182

Passo 2

O desvio padrão é encontrado, para o qual esta equação é usada:

 Ao usar uma calculadora com funções estatísticas, o resultado é imediato:

σ = 1.992

Ou você também pode construir uma tabela, que também é necessária para a próxima etapa e em que cada termo dos resumos que serão necessários é escrito, começando (xYo - X), então (xYo - X)2 E então (xYo - X)4 :

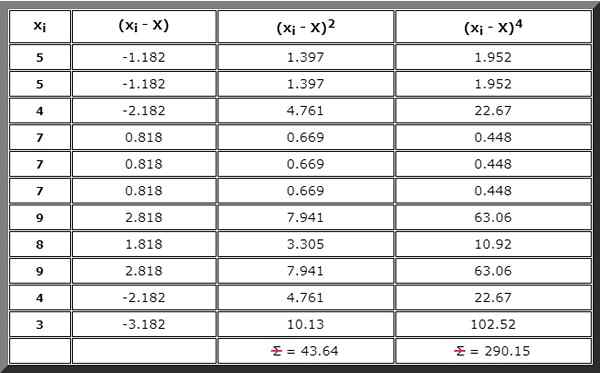
etapa 3

Realizar a soma indicada no numerador de fórmula para g2. Para isso, o resultado da coluna direita da tabela anterior é usada:

∑ (xYo - X)4= 290.quinze

Portanto:

g2 = (1/11) x 290.15/11.9924 = 1.675

O coeficiente de sinalização de Fisher é:

K = g2 - 3 = 1.675 - 3 = -1.325

O que interessa é o sinal do resultado, que, quando negativo, corresponde a um placar de diferentes níveis de dificuldade.

O uso de uma planilha como o Excel facilita muito a resolução desses tipos de problemas e também oferece a opção de representar graficamente a distribuição.

Referências

  1. Levin, r. 1988. Estatísticas para administradores. 2º. Edição. Prentice Hall.
  2. Marco, f. Curtose. Recuperado de: Economipedia.com.
  3. Oliva, J. Assimetria e curtose. Recuperado de: StatisticsAucv.arquivos.WordPress.com.
  4. Spurr, w. 1982. Tomada de decisão na administração. Limusa.
  5. Wikipedia. Curtose. Recuperado de: em.Wikipedia.org.