Quantos diâmetros uma circunferência tem?

Uma circunferência tem diâmetros infinitos. É fácil ver que é assim, se é baseado na definição de diâmetro, que é o segmento que passa simultaneamente pelo centro da circunferência e por dois pontos do mesmo.

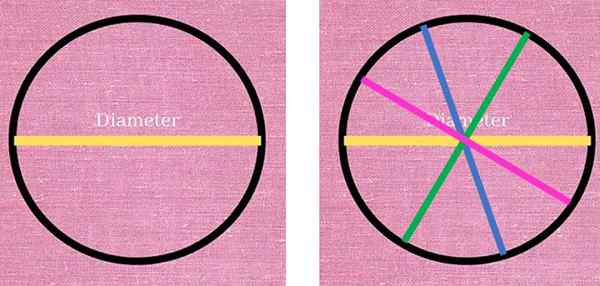
Na figura a seguir, à esquerda, a linha amarela correspondente a um diâmetro da circunferência é observada e dividida em duas partes. No lado direito, três outros diâmetros foram desenhados em cores diferentes: azul, verde e rosa. Todos têm o mesmo comprimento e satisfazem a condição de unir dois pontos da circunferência, através do centro do mesmo.

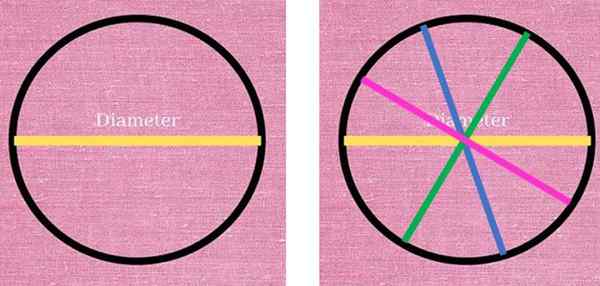O diâmetro é um segmento distinto, que sempre passa pelo centro da circunferência e juntando dois pontos deste. À esquerda, o diâmetro amarelo divide a circunferência em dois. À direita existem outros diâmetros que também dividem a circunferência em duas metades. Fonte: f. Zapata.

Como pode ser visto, as possibilidades de desenhar diâmetros são infinitas, pois infinitas são os pontos que formam a circunferência. O mesmo pode ser afirmado sobre o raio, que é o segmento que une qualquer ponto da circunferência com o centro: um número infinito de rádios pode ser desenhado.

E ao colocar dois rádios opostos um do outro, é obtido um diâmetro, porque o raio mede metade disso.

Diâmetro, comprimento de rádio e circunferência

Seja o diâmetro de qualquer circunferência e r, seu raio. Como o diâmetro mede o dobro do rádio, ele pode ser escrito:

D = 2 ∙ r

Isso significa que, se o raio de um círculo for, por exemplo, r = 5 cm, o diâmetro é d = 2 ∙ 5 cm = 10 cm.

Pode servir a você: Fibonacci Series: Propriedades, Relacionamentos naturais, aplicações

O diâmetro também é conhecido como o Corda principal. As cordas são linhas ou segmentos desenhados entre dois pontos da circunferência, mas que não passam necessariamente pelo centro. Somente o diâmetro tem essa distinção.

Na figura a seguir, você pode ver a diferença e ver por que, na verdade, o diâmetro (vermelho) é o maior das cordas que podem ser desenhadas na circunferência:

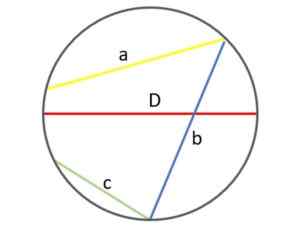Diferentes cordas em uma circunferência: o diâmetro é o maior de todos. Fonte: f. Zapata.

Obviamente, a medida de diâmetro (e, portanto, o raio) é a mesma em uma determinada circunferência. Quando variado, uma circunferência menor ou maior é obtida, de acordo com.

Por outro lado, o tamanho das cordas da mesma circunferência varia, dependendo de quão longe ou perto dos pontos são os pontos que se juntam. No exemplo mostrado, a corda verde “C” é ostensivamente mais curta que as cordas “A” e “B”.

E o número de cordas que podem ser desenhadas também é infinito.

O perímetro da circunferência

Por sua parte, o comprimento da circunferência é equivalente ao seu perímetro ou contorno. Está relacionado ao seu diâmetro, uma vez que quanto maior isso, maior a circunferência (seu perímetro é maior).

A proporção ou quociente entre perímetro e diâmetro é uma constante chamada π (lê "pi"). O valor de π é 3.141592… os pontos suspeitos indicam que a quantidade de decimais e infinitos, o que é porque o Pi é um número irracional. No entanto, para fins práticos, Pi pode simplesmente arredondar 3.14

Pode atendê -lo: quanto você precisa adicionar a 3/4 para obter 6/7?

Se o perímetro for indicado como C e o diâmetro como D, esse motivo será levantado da seguinte forma:

C / d = π

Portanto, a fórmula para a duração da circunferência é:

C = π ∙ D

Ou se preferir com base no raio r:

C = 2π ∙ r

Exemplo ilustrativo

A imagem mostra três circunferências idênticas, designadas com letras A, B e C. Em cada um, a formiga corre a estrada nos segmentos de cores azuis, para ir de um ponto para outro da circunferência.

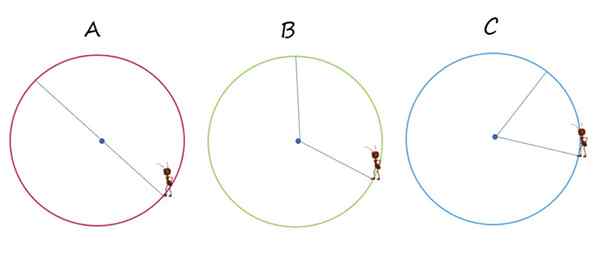A formiga se move de um ponto para outro da circunferência através das linhas azuis mais finas. Fonte: f. Zapata.

1.- Em qual dos casos o deslocamento ocorre exatamente no diâmetro da circunferência?

Responder

Somente no caso A, porque esse caminho passa pelo centro da circunferência e vai de um ponto para outro do mesmo.

2.- Quantos rádios o inseto viaja em cada caso?

Responder

Em qualquer um dos três casos, a formiga viaja dois rádios da circunferência.

3.- Qual dos caminhos corresponde à maior distância?

Responder

A jornada é igualmente longa em cada caso, equivalente a dois rádios da circunferência.

4.- Nesse caso, a formiga está mais longe do seu ponto de partida?

Responder

No caso A, já que é no ponto que está precisamente na frente dele, nos restantes, a formiga está mais próxima do ponto de partida.

5.- E nesse caso a formiga termina a rota mais próxima de seu ponto de origem?

Pode atendê -lo: sinais de agrupamento

Responder

No caso c.

6.- Se o raio das circunferências for de 20 cm, quantos centímetros se medem cada rota?

Responder

Como a formiga percorre uma distância igual a dois rádios, a distância total percorrida é de 40 cm.

Exercícios resolvidos

Exercício 1

Calcule o raio de um círculo cujo diâmetro é 4.5m.

Solução

O rádio é metade do diâmetro, se isso mede 4.5 cm, então o Rádio R é 2.25 cm.

Exercício 2

Encontre o perímetro da circunferência do Exercício 1.

Solução

O perímetro é calculado através do diâmetro ou através do raio, como preferido. No primeiro caso:

C = π ∙ D

Assumindo que π = 3.14 Para rodar, a substituição dos valores fornece o seguinte resultado:

C = π ∙ d = 3.14 ∙ 4.5 cm = 14.13 cm

Exercício 3

Um designer é solicitado a desenhar um logotipo em forma de coração, com as dimensões indicadas na figura. As peças curvas correspondem a semicircums exatos.

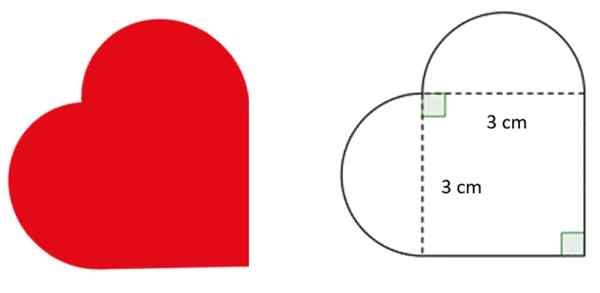
Com esta informação Resposta:

1. Qual é o raio dos semicircunos?
2. Quanto é o perímetro do coração?

Solução para

O diâmetro das semicirferências é equivalente ao lado do quadrado, que é 3 cm. Portanto, seu raio, que é metade, mede 1.5 cm.

Solução b

O perímetro da figura em forma de coração é a soma dos dois lados externos do quadrado e o perímetro das semi -execuções. Como são idênticos, seu perímetro é igual ao de um círculo completo de diâmetro 3 cm:

C = π ∙ d = 3.14 ∙ 3 cm = 9.42 cm

Portanto, o perímetro P da figura é:

P = 9.42 cm + 3 cm + 3 cm = 15.42 cm