Quantas soluções uma equação quadrática tem?

Uma equação quadrática ou equação de segundo grau pode ter zero, uma ou duas soluções reais, dependendo dos coeficientes que aparecem na referida equação. Se você trabalha em números complexos, pode dizer que toda equação quadrática tem duas soluções.

Para iniciar uma equação quadrática, é uma equação do ax²+bx+c = 0 forma, onde a, b e c são números reais e x é uma variável.

Dizem que X1 é uma solução da equação quadrática anterior se, ao substituir x por x1, a equação é satisfeita, ou seja, se a (x1) ²+b (x1)+c = 0.

Se você tem, por exemplo, a equação x²-4x+4 = 0, então x1 = 2 é a solução, pois (2) ² (2) +4 = 4-8+4 = 0.

Pelo contrário, se x2 = 0 for substituído, é obtido (0) ²-4 (0) +4 = 4 e como 4 ≠ 0, então x2 = 0 não é uma solução da equação quadrática.

Soluções de uma equação quadrática

O número de soluções de uma equação quadrática pode ser separado em dois casos que são:

1.- Em números reais

Ao trabalhar com números reais, as equações quadráticas podem ter:

-Zero Solutions: isto é, não há número real que satisfaça a equação quadrática. Por exemplo, a equação dada x²+1 = 0, não há número real tal que satisfaz a referida equação, pois ambos X² é maior ou igual a zero e 1 é maior rigoroso que zero, de modo que sua soma será maior será maior será Rigoroso que zero.

-Uma solução repetida: Existe um único valor real que satisfaz a equação quadrática. Por exemplo, a única solução da equação x²-4x+4 = 0 é x1 = 2.

-Duas soluções diferentes: Existem dois valores que satisfazem a equação quadrática. Por exemplo, x²+x -2 = 0 possui duas soluções diferentes que são x1 = 1 e x2 = -2.

2.- Em números complexos

Ao trabalhar com números complexos, as equações quadráticas sempre têm duas soluções, que são Z1 e Z2 onde Z2 é o conjugado de Z1. Além disso, eles podem ser classificados como:

-Complexos: As soluções são da forma z = p ± qi, onde p e q são números reais. Este caso corresponde ao primeiro caso da lista anterior.

-Complexos puros: É quando a parte real da solução é igual a zero, ou seja, a solução tem a forma z = ± qi, onde q é um número real. Este caso corresponde ao primeiro caso da lista anterior.

-Complexos com parte imaginária igual a zero: É quando a parte complexa da solução é igual a zero, ou seja, a solução é um número real. Este caso corresponde aos dois últimos casos da lista anterior.

Como as soluções de uma equação quadrática são calculadas?

Para calcular as soluções de uma equação quadrática, é usada uma fórmula conhecida como "a resolução", o que diz que as soluções de um AX²+BX+C = 0 equação são dadas pela expressão da seguinte imagem:

A quantidade que aparece dentro da raiz quadrada é chamada discriminante da equação quadrática e é indicada pela letra "d".

A equação quadrática terá:

-Duas soluções reais sim, e apenas sim, d> 0.

-Uma solução real repetida se, e somente se, d = 0.

-Zero soluções reais (ou duas soluções complexas) sim, e apenas sim, d<0.

Exemplos

-As soluções da equação x²+x-2 = 0 são dadas por:

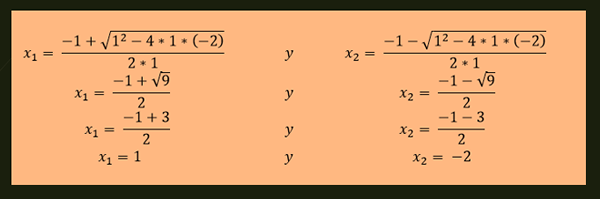
-A equação x²-4x+4 = 0 possui uma solução repetida que é dada por:

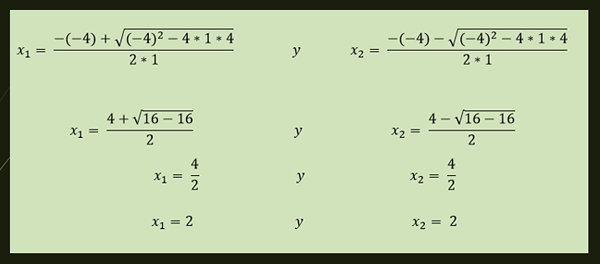
-As soluções da equação x²+1 = 0 são dadas por:

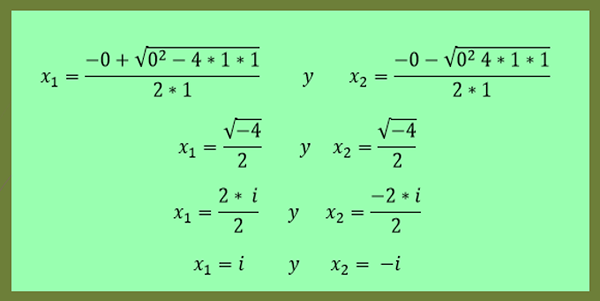
Como pode ser visto neste último exemplo, x2 é o conjugado de x1.