Critérios de triângulos semelhantes

Quais são os critérios de similaridade dos triângulos?

Os critérios de similaridade dos triângulos são as regras que permitem saber se dois triângulos são semelhantes. A semelhança de figuras geométricas, incluindo triângulos, exige que os números tenham a mesma maneira, embora não tenham necessariamente o mesmo tamanho ou a mesma orientação.

Para que dois triângulos sejam semelhantes, é necessário que: i) seus lados homólogos sejam proporcionais e ii) os ângulos internos de cada um têm a mesma medida.

figura 1. Dois triângulos semelhantes: embora eles não tenham o mesmo tamanho, seus lados são proporcionais e seus ângulos internos têm igual medida. Fonte: f. Zapata.

Uma razão proporcional ou proporção entre duas quantidades A e B é representada pela proporção A/B, com B ≠ 0. Para triângulos semelhantes, as seguintes proporções entre os lados são válidos:

a/a '= b/b' = c/c '= r

O valor de R é chamado razão de similaridade.

Além disso, os ângulos internos correspondentes precisam ser da mesma medida, portanto: quina = ero '; Porteb = eroB 'e porte = ϩC'. De acordo com essas condições, os critérios de similaridade dos triângulos são:

Critérios 1: Dois triângulos são semelhantes se tiverem dois ângulos internos de igual medida. Nesse caso, o terceiro ângulo também mede o mesmo, já que a soma dos ângulos internos em qualquer triângulo é 180º:

α = α '; β = β '

Critérios 2: Os triângulos são semelhantes se dois lados homólogos forem proporcionais e o ângulo entre eles for o mesmo:

a/a '= b/b'; α = α '

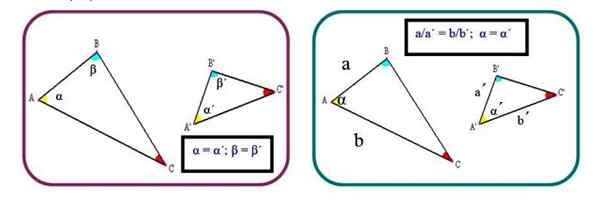Figura 2. Dois critérios para estabelecer a semelhança dos triângulos. Fonte: f. Zapata.

Critérios 3: Os três lados homólogos são proporcionais:

a/a '= b/b' = c/c '= r

Exemplos

A semelhança dos triângulos é muito útil para calcular alturas e distâncias que não são facilmente mensuráveis ​​diretamente. Através de alguns cálculos simples, é possível descobrir esses comprimentos comparando triângulos semelhantes.

Pode servir a você: Teorema Fundamental da Aritmética: Demonstração, Aplicações, Exercícios

Altura de colunas, edifícios e árvores

Dizem que o pai da geometria na Grécia antiga, como Miletus (625-547 para.C.). Com o mesmo método, ele conseguiu medir a altura da grande pirâmide do Egito e, assim, impressionar o faraó.

A distância da lua

Existe um experimento simples que é feito para calcular a distância entre a terra e a lua. Requer uma moeda, um pouco de fita adesiva e um vernier ou uma regra de pós -graduação. Quando a lua está cheia, a moeda é anexada ao copo de uma janela e a lua é observada com um olho, localizado de tal maneira que a moeda cobre apenas a lua cheia.

Quando isso acontece, a razão entre o diâmetro da moeda e a distância entre o olho e a moeda é a mesma que existe entre o diâmetro da lua e a distância entre o olho e a lua:

Diâmetro da moeda/distância da moeda = diâmetro da lua/distância da lua

O motivo é aproximadamente 1/110. O que significa que a distância da lua é 110 vezes o diâmetro deste.

Atualmente, o raio da lua é estimado em 1737.1 km, então seu diâmetro é 3474.2 km. Substituindo esse valor no relacionamento:

Distância da Lua = Diâmetro da Lua ÷ (Diâmetro da moeda/distância da moeda)

Se obtem:

Distância da Lua = 3474.2 km ÷ (1/110) = 382.162 km

Pode servir você: prisma hepagonal

Muito próximo do valor estabelecido por 384 astrônomos.000 km.

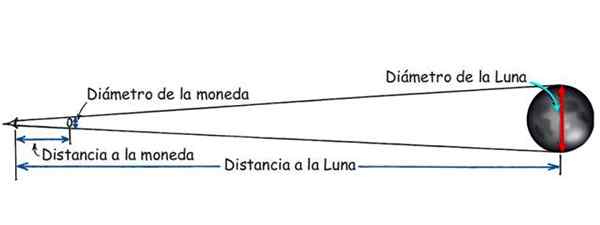Figura 3. A distância da lua pode ser conhecida graças à semelhança dos triângulos. Fonte: Hewitt modificado, P. Física conceitual.

Distância entre um navio e a costa

Para medir a distância entre o navio e a costa, as apostas estão presas na praia nos pontos A, B, C e Q. Os triângulos ABC e PCQ são semelhantes pelos critérios 1, pois têm dois ângulos iguais: os dois ângulos ϩC = α que são opostos pelo vértice e os dois ângulos retos iguais a 90º: ero = ero QQ.

Diz -se que dois triângulos localizados dessa maneira estão em Posição de Thales E eles são sempre semelhantes. Os triângulos são identificados na posição de Thales por ter um ângulo comum e os lados opostos nesse ângulo são paralelos.

Na próxima seção, há um exercício com valores numéricos.

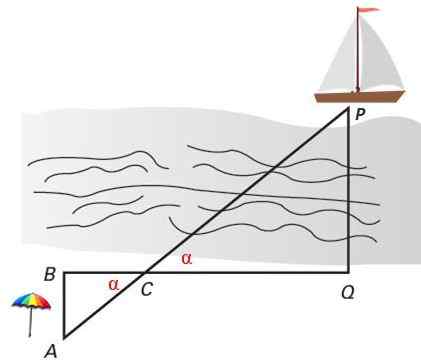Figura 4. Dois triângulos semelhantes na posição de Thales servem para calcular a distância perpendicular de um navio para a costa. Fonte: f. Zapata.

Exercícios resolvidos

Exercício 1

Você quer descobrir até que ponto o veleiro está ancorado na figura anterior, a partir de um ponto localizado na costa da praia, para o qual as apostas são pregadas nos pontos A, B, C e Q, determinando o triângulo ABC, que é semelhante ao PCQ, mas cujos lados são mais fáceis de medir.

Calcule a distância perpendicular PQ entre o navio e a costa, pela semelhança dos triângulos, se as distâncias disponíveis estiverem:

AB = 12 m

BC = 16 m

QC = 60 m

Solução

As proporções entre lados homólogos são:

Ab/qp = bc/cq = 16 m/60 m = 0.267

Portanto 0.267 é a razão da similaridade:

Ab/qp = 0.267

QP = AB / 0.267 = 12 m / 0.267 = 44.9 m

Exercício 2

No triângulo seguinte: quanto o segmento de anúncios mede?

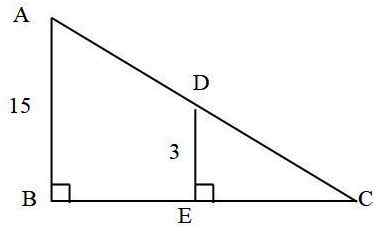
Sabe -se disso:

• CA = 25 cm
• AB = 15 cm
• DE = 3 cm

Pode atendê -lo: múltiplos de 2: o que são e explicação

Solução

Os triângulos são semelhantes, porque compartilham um ângulo que é ero e os lados de e ab são paralelos. A taxa de similaridade é calculada por:

R = ab / de = 15 cm / 3 cm = 5

E também através de:

R = AC / DC

Portanto, dc = ac / r = 25 cm / 5 = 5 cm

Sendo que:

AC = AD + DC

Segue -se que ad = ac - dc = 25 cm - 5 cm = 20 cm

Exercício 3

Um triângulo isósceles tem um perímetro de 49 cm e uma base de 21 cm. Calcule o perímetro de um triângulo semelhante a este, mas cuja base mede 4 cm.

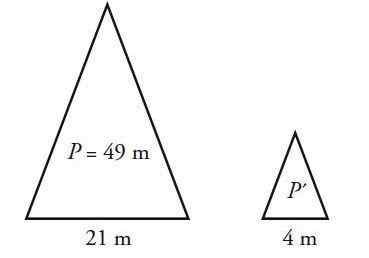
Solução

O triângulo isosceles tem dois lados iguais, diferente da base B. Vamos a medida dos lados e P o perímetro, que consiste na soma dos três lados. Para o maior triângulo:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Agora, a proporção entre os lados dos triângulos é levantada, as do pequeno triângulo são simbolizadas com prêmios:

B/ b '= ℓ/ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

O perímetro do pequeno triângulo será:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Hewitt, Paul. 2012. Ciência física conceitual. 5 ª. Ed. Pearson.
3. Clemens, s. Geometria com aplicações. Addison Wesley.
4. Ibáñez, p. 2010. Matemática III. Cengage Learning.
5. Jiménez, r. Matemática II: Geometria e Trigonometria. 2º. Edição. Pearson.
6. Stewart, J. 2007. Pré -cálculo. 5 ª. Edição. Cengage Learning.
7. Vicmat. Samos Aristarco: medidas do sistema solar. Recuperado de: vicmat.com