Boltzmann História constante, equações, cálculo, exercícios

O Boltzmann constante É o valor que relaciona a energia cinética média de um sistema termodinâmico ou um objeto com a temperatura absoluta do mesmo. Embora muitas vezes estejam confusos, a temperatura e a energia não são o mesmo conceito.

A temperatura é uma medida de energia, mas não a própria energia. Com a constante de Boltzmann, uma está ligada uma com a outra da seguinte forma:

E_c = (3/2) k_B  T

Boltzmann anfitrião em Viena. Fonte: Dadotet na Wikipedia inglesa [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

Esta equação é válida para uma molécula de gás monoatômica ideal m, onde E_c É sua energia cinética dada em Joules, k_B É constante de Boltzmann e T É a temperatura absoluta em Kelvin.

Dessa forma, quando a temperatura aumenta, a energia cinética média por molécula de substância também aumenta, conforme o esperado acontecer. E o oposto acontece quando a temperatura diminui, sendo capaz de atingir o ponto em que todo o movimento cessa, a temperatura mais baixa possível ou absoluta é atingida.

Ao falar sobre energia cinética média, é necessário lembrar que a energia cinética está associada ao movimento. E as partículas podem se mover de várias maneiras, por exemplo, movendo, girando ou vibrando. Obviamente, nem todos farão isso da mesma maneira e, como são incontáveis, a média é levada para caracterizar o sistema.

Alguns estados de energia são mais propensos do que outros. Este conceito é de importância radical na termodinâmica. A energia considerada na equação anterior é a energia cinética da tradução. Da probabilidade dos estados e seu relacionamento com a constante Boltzmann falará um pouco mais tarde.

Em 2018, o Kelvin foi redefinido e com ele a constante Boltzmann, que no sistema internacional é aproximadamente 1.380649 x 10^-23 J. K^-1. Muito mais precisão pode ser alcançado para a constante Boltzmann, que foi determinada em vários laboratórios em todo o mundo, por diferentes métodos.

[TOC]

História

A famosa constante deve seu nome ao físico Ludwig Boltzmann (1844-1906), nascido em Viena, que dedicou sua vida como cientista ao estudo do comportamento estatístico dos sistemas com muitas partículas, do ponto de vista da mecânica newtoniana.

Embora hoje a existência do átomo seja universalmente aceita, no século XIX, a crença sobre se o átomo realmente existia ou era um artifício com o qual muitos fenômenos físicos foram explicados estavam em pleno debate em pleno.

Pode atendê -lo: vetor normal: cálculo e exemplo

Boltzmann foi um forte defensor da existência do átomo e, em seu tempo, ele enfrentou duras críticas a seu trabalho por muitos colegas, que consideravam que eles continham paradoxos insolúveis.

Ele declarou que fenômenos observáveis ​​em níveis macroscópicos poderiam ser explicados através das propriedades estatísticas de partículas constituintes, como átomos e moléculas.

Essa crítica pode ser devido ao profundo episódio de depressão que o levou a tirar a própria vida no início de setembro de 1906, quando ele ainda tinha muito o que fazer, porque ele era considerado um dos grandes físicos teóricos de seu tempo e ali e ali foi pouco para que outros cientistas contribuirão para corroborar a veracidade de suas teorias.

Isso não aconteceu muito tempo depois de sua morte, quando novas descobertas sobre a natureza do átomo e suas partículas constituintes seriam adicionadas para dar o motivo a Boltzmann.

Constant de Boltzmann e as obras de Planck

Agora, a constante de Boltzmann k_B Foi introduzido como é conhecido hoje um pouco depois do trabalho do físico austríaco. Era Max Planck, em sua lei da emissão do corpo negro, um trabalho que ele apresentou em 1901, que na época lhe deu o valor de 1,34 x 10²³ J/k.

Até o ano de 1933, Boltzmann foi adicionado a Viena como um tributo a uma placa com a definição de entropia envolvendo a famosa constante: S = k_B log w, equação que será discutida mais tarde.

Hoje, a constante de Boltzmann é indispensável na aplicação das leis termodinâmicas, mecânica estatística e teoria da informação, campos dos quais esse físico com fim triste foi pioneiro.

Valor e equações

Os gases podem ser descritos em termos macroscópicos e também em termos microscópicos. Para a primeira descrição, existem conceitos como densidade, temperatura e pressão.

No entanto, deve -se lembrar que um gás é composto de muitas partículas, que têm uma tendência global a um certo comportamento. É essa tendência que é medida macroscopicamente. Uma maneira de determinar a constante de Boltzmann é graças à equação bem conhecida dos gases ideais:

p.V = n. R. T

Aqui p É pressão do gás, V É o seu volume, n É o número de toupeiras presentes, R É a constante dos gases e T É a temperatura. Em um mol de gás ideal, a seguinte relação entre o produto é cumprida p.V, e a energia cinética da tradução K Todo o conjunto é:

Pode atendê -lo: modelo corpuscular de matéria

p.V = (2/3). K

Portanto, a energia cinética é:

K = (3/2) n.R.T

Ao dividir o número total de moléculas presentes, que serão chamadas de N, a energia cinética média de uma única partícula é obtida:

E_c = K /n

E_c= (3/2n) n.R.T

Em um mol, há o número de partículas n_PARA, E, portanto, o número total de partículas é N = nnA, ficando:

E_c = (3/2nn_PARA) n.R.T

Precisamente o quociente R/n_PARA É constante de Boltzmann, demonstrando que a energia cinética da tradução média de uma partícula depende apenas da temperatura absoluta e não de outras magnitudes, como pressão, volume ou mesmo do tipo de molécula:

E_c = (3/2) k_B. T

Constante e entropia de Boltzmann

Um gás tem uma determinada temperatura, mas essa temperatura pode corresponder a diferentes estados de energia interna. Como visualizar essa diferença?

Considere o lançamento simultâneo de 4 moedas e as maneiras pelas quais eles podem cair:

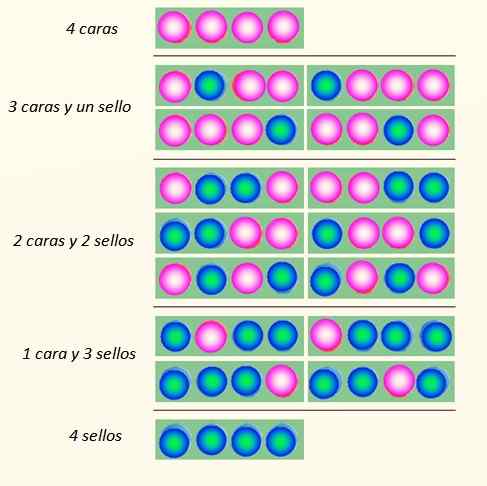Maneiras pelas quais 4 moedas podem cair. Fonte: Self feito

O conjunto de moedas pode assumir um total de 5 estados, que são considerados Macroscópico, descrito na figura. Qual desses estados o leitor diria que é o mais provável?

A resposta deve ser o estado de 2 faces e 2 cruzamentos, porque tem um total de 6 possibilidades, dos 16 ilustrados na figura. E 2⁴ = 16. Estes são equivalentes aos estados microscópico.

E se 20 moedas forem lançadas em vez de 4? Haveria um total de 2^vinte possibilidades ou "estados microscópicos". É um número muito maior e mais difícil de lidar. Para facilitar o gerenciamento de grandes números, os logaritmos são muito apropriados.

Agora, o que parece evidente é que o estado com o maior distúrbio é o mais provável. Os estados mais ordenados como 4 rostos ou 4 selos são um pouco menos propensos.

A entropia de um estado macroscópico S é definido como:

S = k_B ln w

Onde C É o número de estados microscópicos possíveis e k_B É constante de Boltzmann. Como ln w É adimensional, a entropia tem as mesmas unidades que K_B: Joule/k.

Esta é a famosa equação na lápide de Boltzmann em Viena. No entanto, mais do que entropia, o relevante é a mudança dela:

Pode atendê -lo: variáveis ​​termodinâmicas: quais são e exercícios resolvidos

ΔS = k_B ln w₂ - k_B ln w₁ = k_B ln (w₂/c₁)

Como K é calculado_B?

O valor da constante de Boltzmann é obtido experimentalmente precisamente com medições com base em Termometria acústica, que são realizados usando a propriedade que estabelece a dependência da velocidade do som em um gás com a temperatura do mesmo.

De fato, a velocidade do som em um gás é dada por:

Onde b _adiabático É o módulo de compressibilidade adiabática dado por:

B_adiabático = γp

E ρ é densidade de gás. Para a equação anterior, p É a pressão do gás em questão e γ É o coeficiente adiabático, cujo valor para um gás específico é encontrado em tabelas.

Institutos de metrologia também experimentam outras maneiras de medir a constante, como Termometria de ruído Johnson, que usa as flutuações térmicas que ocorrem aleatoriamente nos materiais, em particular em drivers.

Exercícios resolvidos

-Exercício 1

Encontrar:

a) A energia cinética da tradução média E_c que tem uma molécula de gás ideal a 25 ºC

b) A energia cinética da tradução K das moléculas em 1 mol deste gás

c) A velocidade média de uma molécula de oxigênio a 25 ºC

Facto

m_oxigênio = 16 x 10 ^-3 kg/mol

Solução

para) E_c = (3/2) k t = 1.5 x 1.380649 x 10^-23J. K^-1 x 298 K = 6.2 x 10^{-vinte e um} J

b) K = (3/2) n.R.T = 5 x 1 mol x 8.314 J/mol .K x 298 K = 3716 J

c) E_c = ½ mv², Levando em consideração que a molécula de oxigênio é diatômica e a massa molar deve ser multiplicada por 2, será: será:

-Exercício 2

Encontre a mudança de entropia quando 1 mol de gás ocupado com um volume de 0.5m³ Ele se expande para ocupar 1 m³.

Solução

ΔS = k_B ln (w₂/c₁)

C₂= 2^NC₁ (Havia 2⁴ Estados microscópicos para o lançamento das 4 moedas, lembre -se?)

Onde n é o número de partículas presentes em 0.5 mol de gás 0.5 x n_PARA:

ΔS = k_B LN (2^N C₁/c₁) = k_B LN 2^N= k_B 0.5n_PARA Ln 2 = 2.88 J/K

Referências

1. Atkins, p. 1999. Química Física. Edições Omega. 13-47.
2. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill. 664-672.
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º ... Ed Prentice Hall. 443 -444.
4. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1. 647-673.
5. Se redefinição. Kelvin: Boltzmann Constant. Recuperado de: nist.Gov