Conceito de condições de equilíbrio, aplicações e exemplos

As condições de equilíbrio Eles são necessários para que um corpo permaneça em repouso ou em movimento retilíneo uniforme. No primeiro caso, diz -se que o objeto está em equilíbrio estático, enquanto no segundo está em equilíbrio dinâmico.

Supondo que o objeto móvel seja uma partícula; nesse caso, as dimensões não são levadas em consideração, basta que a soma das forças que atuam nele seja anulada.

figura 1. As rochas de Brimham, ao norte da Inglaterra, atendem às condições de equilíbrio. Fonte: Public DomainParturas.líquido.

Mas uma grande maioria dos objetos móveis tem dimensões apreciáveis; portanto, essa condição não é suficiente para garantir o equilíbrio, o que em qualquer caso é a ausência de aceleração, não de movimento.

[TOC]

Primeiro e segunda condição de equilíbrio

Vamos ver: se a soma das forças é anulada, é verdade que o objeto não vai se mover ou se mover rapidamente, mas ainda pode começar a virar.

Portanto, para evitar rotações, uma segunda condição deve.

Em suma, denotando como F A força líquida e τ qualquer M Para o vetor de torque líquido, teremos:

Primeira condição de equilíbrio

∑ F = 0

O que significa que: ∑ f_x = 0, ∑ f_e = 0 e ∑ f_z = 0

Segunda condição de equilíbrio

∑ τ = 0 ou ∑ M = 0

Com torques ou momentos calculados em relação a qualquer ponto.

A seguir, assumiremos que o objeto móvel é um corpo rígido, que não experimenta nenhuma deformação.

Formulários

Embora o movimento pareça ser o denominador comum no universo, o equilíbrio também está presente em muitos aspectos da natureza e nos objetos que nos cercam.

Pode servir a você: Millikan Experiment: Procedimento, Explicação, Importância

Equilíbrio isostático

Em uma escala planetária, a Terra está em Equilíbrio isostático, Um tipo de equilíbrio gravitacional da crosta terrestre, cuja densidade não é uniforme.

As diferenças nas densidades dos diferentes blocos ou áreas da crosta terrestre são compensadas com as diferenças de altura que caracterizam a orografia do planeta. Funciona da mesma maneira que diferentes materiais submertam mais ou menos em água de acordo com sua densidade e alcançam o equilíbrio.

Mas como os blocos de casca não flutuam na água, mas no manto, o que é muito mais viscoso, o equilíbrio não é chamado de hidrostático, mas isostático.

Operação de fusão no núcleo

Nas estrelas como o nosso Sol, o equilíbrio entre a força da gravidade que as comprime e a pressão hidrostática que os expande, mantém o reator de fusão em operação no núcleo da estrela, o que o mantém vivo. Dependemos desse equilíbrio para que a Terra receba a luz e o calor necessários.

Construção

Em escala local, queremos que edifícios e construções permaneçam estáveis, ou seja, as condições de equilíbrio obedecem, em particular o equilíbrio estático.

É por isso que surgiu a estática, que é o ramo da mecânica dedicada a estudar o equilíbrio dos corpos e tudo o que é necessário para mantê -los assim.

Tipos de equilíbrio estático

Na prática, descobrimos que o equilíbrio estático pode ser de três classes:

Equilíbrio estável

Ocorre quando o objeto se move de sua posição e imediatamente retorna a ele quando a força que o afastou. Quanto mais próximo um objeto do solo, maior a probabilidade de estar em equilíbrio estável.

Pode servir a você: densidade aparente: fórmula, unidades e exercícios resolvidos

A bola direita na figura 2 é um bom exemplo, se a retirarmos de sua posição de equilíbrio na parte inferior da tigela, a gravidade será responsável por retornar rapidamente.

Equilíbrio indiferente ou neutro

Ocorre quando o objeto, apesar de ser movido, continua em equilíbrio. Objetos redondos como a bola, quando colocados em superfícies planas estão em equilíbrio indiferente.

Equilíbrio instável

Ocorre quando o objeto se move de sua posição de equilíbrio, não retorna a ele. Se mantivermos a bola à beira da colina à esquerda, é certo que ela não retornará por seus próprios meios.

Figura 2. Tipos de equilíbrio. Fonte: Wikimedia Commons.

Exemplo: Partícula estática

Suponha que um bloco de massa m Em um plano inclinado, que deveria estar concentrado em seu centro geométrico.

O componente horizontal do peso w_x Tende a fazer o bloco escorregar, portanto, outra força que se opõe. Se queremos que o bloco fique em repouso, essa força é um atrito estático. Mas se permitirmos que o bloco deslize ladeira abaixo com velocidade constante, a força necessária é o atrito dinâmico.

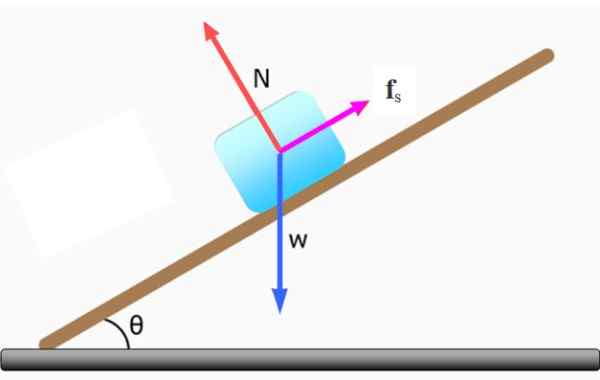Figura 3. Um bloco permanece em equilíbrio estático no plano inclinado. Fonte: f. Zapata.

Na ausência de atrito, o bloco deslizará para baixo e, nesse caso, não haverá equilíbrio.

Para que o bloco esteja em repouso, as forças agindo sobre ele: peso C, O normal N e atrito estático F_s, Eles devem ser compensados. Então:

∑ f_e = 0 → N - W_e = 0

∑ f_x = 0 → W_x - F_s = 0

O atrito estático equilibra o componente horizontal do peso: W_x = f_s E por tanto:

F_s = m . g .sin θ

Exercício resolvido

Um semáforo de 21.5 kg pendura de uma barra de alumínio AB homogênea de 12 kg de massa e 7.5 m de comprimento, sustentado por uma corda horizontal de CD, como mostrado na figura. Encontrar:

Pode atendê -lo: Teorema da sobreposição: Explicação, Aplicações, Exercícios resolvidos

a) Tensão do cabo do CD

b) os componentes horizontais e verticais da força exercida pelo pivô no poste.

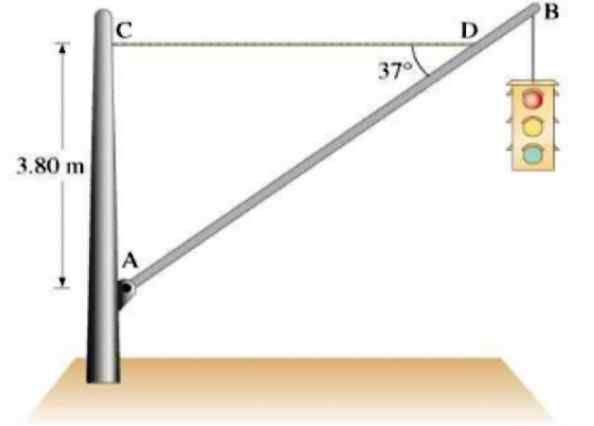Figura 4.- Um semáforo está pendurado em uma barra de alumínio em equilíbrio estático. Fonte: Giancoli. D. Física com aplicações.

Solução

O diagrama das forças aplicado à barra é construído, com o peso C, As tensões nas cordas e os componentes horizontais e verticais da reação do pivô, chamados r_x e r_e. Então as condições de equilíbrio se aplicam.

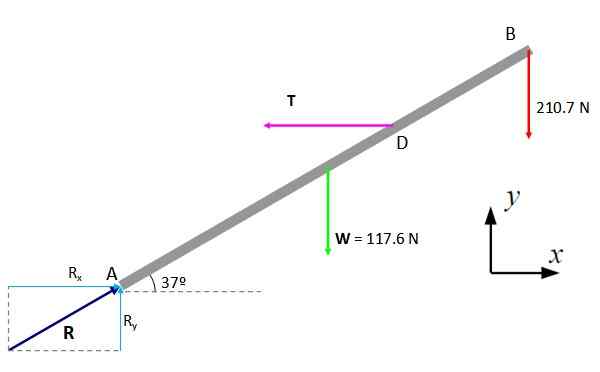Figura 5. Diagrama de corpo livre para o bar. Fonte: f. Zapata.

Primeira condição

Sendo um problema no avião, a primeira condição de equilíbrio oferece duas equações:

Σf_x = 0
Σf_e = 0

Desde o primeiro:

R_x - T = 0

R_x = T

E do segundo:

R_e - 117.6 n - 210.7 n = 0

R_e = 328.3 n

O componente horizontal da reação é de igual magnitude como a tensão T.

Segunda condição

O ponto A da Figura 5 é escolhido como um centro de turno, dessa maneira o braço de reação R É nulo, lembre -se de que a magnitude do momento é dada por:

M = f_┴ d

Onde f_┴ É o componente perpendicular da força e D é a distância entre o eixo de rotação e o ponto de aplicação da força. Teremos uma equação:

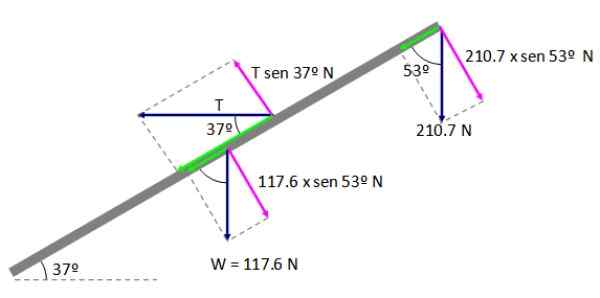Figura 6. Momentos sobre o ponto A. Fonte: f. Zapata.

Σm_PARA = 0

(210.7 × sen 53º) AB + (117.6 × sen 53º) (ab/2) - (t × sen 37º) ad = 0

O anúncio de distância é:

Ad = (3.8 m / sin 37º) = 6.3 m

(210.7 × sen 53º N) (7.5 m) + (117.6 × sen 53º N) (3.75 m) - (t × sen 37º N) (6.3 m) = 0

Executando as operações indicadas:

1262.04 + 352.20 - 3.8t = 0

Limpando T recebe:

T = 424.8 n

Desde a primeira condição, teve que_x = T, portanto:

R_x = 424.8 n

Assuntos de interesse

Primeira condição de equilíbrio.

Segunda condição de equilíbrio.

Referências

1. Bedford, 2000. PARA. Mecânica para engenharia: estático. Addison Wesley.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 4. Sistemas de partículas. Editado por Douglas Figueroa (USB).
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.
5. Wikipedia. Isostasia. Recuperado de: é.Wikipedia.org.