Como obter a porcentagem? Exemplos e exercícios

Se pode Obtenha uma porcentagem Com vários métodos. Você pode calcular rapidamente 10% de qualquer número apenas ao mover sua vírgula decimal em uma posição para a esquerda. Por exemplo, 10% de 100 é 10; 10% de 1000 é 100.

Se você deseja calcular porcentagens mais complexas, como 36% de 25 ou 250% de 20, outros métodos são necessários. Para os casos em que o sistema de 10% não é aplicável, as seguintes metodologias podem ser levadas em consideração.

figura 1. Descontos com porcentagens diferentes. Quanto nós nos salvamos?. Fonte: Pixabay.

O termo porcentagem significa uma certa parte de cada cem e refere -se à operação aritmética que é realizada para encontrar a referida parte. Por exemplo, 20% ("vinte por cento") é lido em pesos, significa que 20 pesos são descontados para cada 100 pesos.

A porcentagem serve para calcular qual parte do total representa uma quantidade. Nesse caso, o total é levado para a escala de 100 e a porcentagem informa quanto, com base nos 100, é a parte que deve ser calculada.

Vamos ver como isso é feito com esses exemplos. Em primeiro lugar, fazemos isso na forma de uma fração:

• 20% = 20/100
• 5% = 5 /100
• 0,7% = 0,7 / 100
• 100% = 100 /100

Observe que 100% é igual a 1. Mas as porcentagens também podem ser escritas decimais:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

Quando a porcentagem de um determinado número é expressa, simplesmente A vírgula se move Daquele número dois lugares à esquerda. Na porcentagem, o regra de proporcionalidade:

20% são 20 em 100, portanto:

20% de 100 é 20, 20% de 200 é 40, 20% de 300 é 60, 20% de 50 é 10.

Regra geral para 20 % de qualquer quantia

20% de x é x *(20/100) = x *0,2 = 0,2 *x

Esta regra pode se estender facilmente para encontrar qualquer outra porcentagem desejada. Vamos ver como na seção seguinte.

Exercício resolvido com fórmula para calcular n% 

Uma fórmula para resumir o mais rápido possível e calcular rapidamente qualquer porcentagem n é:

n % =(A * n)/100

Por exemplo, você deseja calcular 25% de 400

Então n = 25 e a = 400, resultando em (400*25)/100 = 100

Exemplo

Qual porcentagem de 60 é 24?

Solução

O que é solicitado é equivalente a perguntar o que é o n% de 60 que dá 24?

Propomos a fórmula geral:

60 * n / 100 = 24

Nós limpamos n Com este procedimento:

-Os 100 que estão se dividindo no membro IZiédo De igualdade, vá para o membro direito multiplicando. 

-E os 60 que se multiplica no membro esquerda Vá para o membro direito dividindo.

N = 24 *100 /60 = 2400 /60 = 240/6 = 6 *40 /6 = 40

Conclui -se que 40% de 60 é 24.

Exercícios de cálculo percentual resolvidos 

Abaixo estão exercícios simples para começar a praticar o mencionado.

Pode atendê -lo: as 15 lendas e mitos mais populares

Exercício 1

Encontre 50% de 90.

Solução

Aqui x = 90, n = 50 % e substitua:

90 * 50% = 90 * (50 /100) = 4500 /100 = 45 

Isso é bastante simples, porque 50 % de qualquer quantidade é metade dessa quantidade e metade de 90 é 45.

Exercício 2

Encontre 30% de 90.

Solução

90 * 30% = 90 * (30/10) = 2700 /100 = 27

Aumentos percentuais

É frequente na vida cotidiana ouvir o aumento de algo, por exemplo, um aumento na produção, um aumento salarial ou a ascensão de um produto. Quase sempre é expresso em forma de porcentagem.

Por exemplo, um certo produto custou € 300, mas sofreu um aumento de 30%. Perguntamos a nós mesmos: qual é o novo preço do produto?

O primeiro é calcular a parte que corresponde ao aumento. Como o aumento é de 30 partes de 100, o aumento do aumento, com base no preço original de 300, é três vezes as 30 partes, ou seja, 3*30 = 90.

O produto aumentou € 90, portanto, o novo preço final será o que custou o aumento antes:

Novo preço = preço antigo + € 90 = € 390

Podemos construir uma fórmula para o cálculo do aumento percentual. Usamos cartas para simbolizar preços, assim:

-F é o valor final

-Yo é o valor inicial e

-n é o aumento do aumento.

Com esses nomes, o valor final seria calculado assim:

f = i + (i* n / 100)

Mas como Yo É repetido em ambos os termos, pode ser tomado como um fator comumPara obter essa outra expressão, igualmente válida:

F = i * (1 + n / 100)

Vamos verificar com o caso já resolvido, o produto que custou 300 euros e aumentou 30%. Assim, garantimos que a fórmula funcione bem:

Preço final = F = € 300 * (1 + 30/100) = € 300 * (1 + 0,3) = € 300 * 1,3 = € 390

Exercício 3

Um funcionário ganhou € 1500, mas foi promovido e seu salário teve um aumento de 20%. Qual é o seu novo salário?

Solução

Vamos aplicar a fórmula:

F = € 1500 * (1 + 20/100) = € 1500 * (1 + 0,2) = € 1500 * 1,2 = € 1800

O novo salário do funcionário é de € 1800.

A porcentagem diminui

No caso de diminuição, a fórmula para o cálculo do valor final F de um certo valor inicial Yo que sofreu uma diminuição em n% é:

F = i * (1 - n / 100)

Deve-se notar que o sinal positivo (+) da fórmula na seção anterior foi substituído por um sinal negativo (-).

Figura 2. Aviso de desconto percentual. Fonte: Pixabay

Exercício 4

Um produto marcou € 800, mas recebeu um desconto de 15%. Qual é o novo preço do produto?

Solução 4

O preço final de acordo com a fórmula é:

F = € 800 * (1 - 15/10) = € 800 * (1 - 0,15) = € 800 * (0,85) = € 680

O preço final com o desconto de 15% é de € 680, o que representa uma economia de € 120.

Porcentagens sucessivas

Parece que quando alguma quantidade sofre uma variação percentual e depois outra é aplicada, também uma porcentagem. Por exemplo, um produto que teve dois descontos percentuais consecutivos. Outro exemplo é o de um funcionário que teve dois aumentos de salário consecutivos.

Pode atendê -lo: atividades econômicas mais importantes de Yucatan

- Aumentos percentuais sucessivos

A base de solução desses casos é a mesma que os aumentos únicos, mas deve -se levar em consideração que o segundo aumento percentual é realizado no valor final do primeiro aumento.

Suponha que um produto que aumentou primeiro 10% e depois 5%. É incorreto dizer que sofreu um aumento de 15%, na verdade era mais do que essa porcentagem.

As fórmulas para o valor final se aplicariam assim:

-Primeiro, o valor final do primeiro aumento de N1% é calculado

f1 = i + i * n1 / 100

-E então, para encontrar o valor final do segundo aumento de N2%, o valor final de F1 é considerado um valor inicial. Portanto:

F2 = f1 + f1 * n2 /100 

Exercício 5

Um livro originalmente custou € 55, mas devido ao seu sucesso e alta demanda, sofreu dois aumentos consecutivos no preço original. O primeiro aumento foi de 10% e o segundo de 20%. Qual é o preço final do livro?

Solução

-Primeiro aumento:

F1 = € 55 * (1 + 10 /100) = € 55 * 1,1 = € 60,5

-Segundo aumento

F2 = € 60,5 * (1 + 20/100) = € 60,5 * 1.2 = € 72,6

O preço final é de € 72,6.

Exercício 6

Em referência ao exercício anterior. Os dois aumentos consecutivos: a qual porcentagem de um aumento único sobre o preço do livro original corresponde?

Solução

Se ligarmos para n% para a porcentagem de aumento exclusivo, a fórmula que relaciona esse aumento percentual exclusivo ao valor original e o valor final é:

F2 = i *(1 + n / 100) 

Quer dizer:

€ 72,6 = € 55 + 55 € * (n / 100)

Limpando o aumento do aumento de n% = (n /100), temos:

(N / 100) = (€ 72,6 - € 55) / 55 € = 17.€ 6 / € 55 = 0,32

Portanto:

N = 0,32 * 100 = 32

Ao preço do livro, um aumento percentual total de 32% foi aplicado. Observe que esse aumento é maior que a soma dos dois aumentos percentuais consecutivos.

- Descontos percentuais sucessivos

A idéia é semelhante à de sucessivas porcentagens aumentos. O segundo desconto percentual sempre deve ser aplicado ao valor final do primeiro desconto, vejamos um exemplo:

Exercício 7

Um desconto de 10% seguido de um segundo desconto de 20% em um objeto, para o qual o desconto percentual exclusivo é equivalente?

Solução

-Primeiro desconto:

F1 = i - i * n1 / 100  

-Segundo desconto

F2 = F1 - F1 * N2 / 100

Substituindo a primeira equação no segundo restos:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Desenvolvendo essa expressão, obtemos:

f2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Desenho de fator comum Yo:

f2 = i * (1- n1% - n2% + n1% * n2%)

Finalmente, as porcentagens indicadas na questão são substituídas:

F2 = i * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = i * (1 - 0.28) = i * (1 - 100/10) = i * (1 - 28%)

Em outras palavras, descontos sucessivos de 10% e 20% correspondem a um desconto exclusivo de 28%.

Exercícios avançados

Vamos tentar esses exercícios apenas quando as idéias dos anteriores foram claras o suficiente.

Pode servir a você: capas geográficas fáceis e bonitas, capas, imagens

Exercício 8

A base de um triângulo mede 10 cm e altura 6 cm. Se o comprimento da base diminuir em 10%. Em que porcentagem a altura deve ser aumentada para que a área do triângulo não mude?

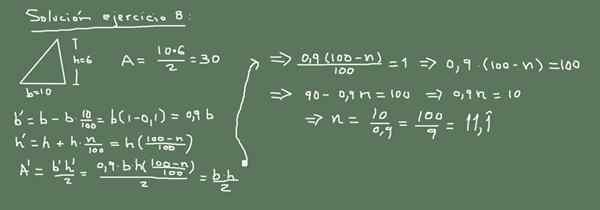Figura 3. Solução alternativa para o exercício 8. Preparado por f. Zapata.

Solução 8

A área original do triângulo é:

A = (10cm * 6cm) / 2 = 30 cm²

Agora, se a base diminuir em 10%, seu novo valor é:

Nova base = 10 - (10/100) x 10 = 9 cm.

O novo valor da altura será x e a área original deve permanecer inalterada, de modo que:

(9cm * x) /2 = 30 cm²

Então o valor de x é limpo como:

X = 60 cm² / 9 cm = (20/3) cm = 6.666 cm

O que significa um aumento de 0,666 em comparação com o valor original. Vamos ver agora qual a porcentagem disso representa:

6.666 = 6 + (6 * n/100) 

6.666 -6 = 6 * n/100

0.666 = 6 * N/100

N/100 = 0,111

N = 11.1

A resposta é: a altura deve ser aumentada em 11,1% para a área do triângulo permanecer a mesma.

Exercício 9

Se o salário for aumentado em 20%, mas os descontos de impostos descontos em 5%, qual é o aumento real que o trabalhador recebe?

Solução 

Primeiro, calculamos o aumento de N1%:

f1 = i + i * n1 / 100

Em seguida, aplicamos o desconto de N2%:

F2 = F1 - F1 * N2 / 100

A primeira equação é substituída no segundo:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

A expressão anterior se desenvolve:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Finalmente é removido Yo Fator comum e os valores de n1 = 20 e n2 = 5 que aparecem na declaração são substituídos:

F2 = i (1 + 0,2 - 0,05 - 0,2* 0,05) = i* (1 + 7/50) = i* (1 + 14/100) = i* (1 + 14%)

O trabalhador recebeu um aumento líquido de 14%.

Exercício 10

Decida o que é mais conveniente entre essas duas opções:

i) adquirir camisas T com um desconto de 32 % cada.

Ii) Compre 3 shirts pelo preço de 2.

Solução 

Analisamos cada opção separadamente e depois escolhemos o mais econômico:

i) Seja x o preço atual de uma camisa, um desconto de 32 % representa um preço final do XF:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Por exemplo, comprar 3 camisas significa gastar 3 x 0.68 x = 2.04x

ii) Se x é o preço de uma camisa, por 3 camisas, você simplesmente pagará 2x.

Suponha que uma camisa vale 6 euros, com o desconto de 32 % que valeria 4.08 Euros. Comprar 1 t -shirt não é uma opção válida na oferta 3 × 2. Então, se você quiser comprar apenas 1 camisa, o desconto é preferível.

Mas se o que você quer é comprar por dezenas, a oferta 3 × 2 é apenas um pouco mais barata. Por exemplo, 6 t -shirts com o desconto sairiam para 24.48 euros, enquanto com a oferta 3 × 2, eles custariam 24 euros

Referências

1. Sala de aula fácil. A porcentagem. Recuperado de: sala de aula.com
2. Baldor a. 2006. Aritmética teórica prática. Edições culturais.
3. Crianças educadas. Como aprender a calcular porcentagens. Recuperado de: Educaipeques.com
4. Gutiérrez, g. Notas de matemática financeira. Recuperado de: csh.Izt.Uam.mx
5. Ticks inteligentes. Porcentagem: o que é e como é calculado. Recuperado de: Smartick.é