Como obter o ângulo de um triângulo? (Exemplo)

Existem várias maneiras de Calcule os lados e ângulos de um triângulo. Estes dependem do tipo de triângulo com o qual você está trabalhando.

Nesta ocasião, será mostrado como calcular os lados e os ângulos de um triângulo direito, assumindo que certos dados do triângulo com conhecidos com conhecidos.

Os elementos que serão usados ​​são:

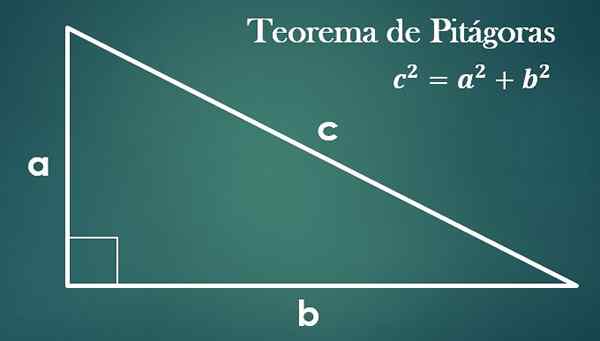
- Teorema de Pitágoras

Dado um triângulo retângulo com "a", "b" e hipotenusa "c", é verdade que "c² = a²+b²".

- Área de um triângulo

A fórmula para calcular a área de qualquer triângulo é a = (b × h)/2, onde "b" é o comprimento da base e "h" o comprimento da altura.

- Ângulos de um triângulo

A soma dos três ângulos internos de um triângulo é de 180 °.

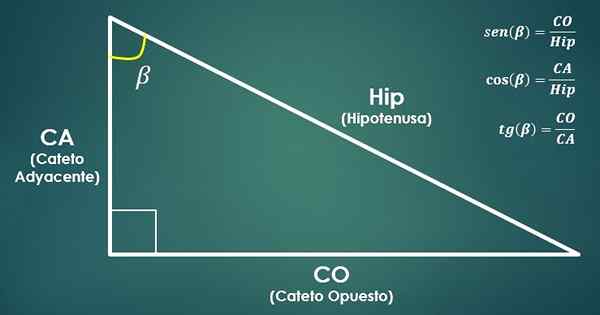
- Funções trigonométricas:

Considere um triângulo certo. Em seguida, as funções trigonométricas são definidas em seio, cosseno e tangente do ângulo beta (β) da seguinte forma:

sin (β) = co/hyp, cos (β) = ca/quadril e tan (β) = co/ca.

Como calcular os lados e ângulos de um triângulo direito?

Dado um triângulo retângulo ABC, as seguintes situações podem ser apresentadas:

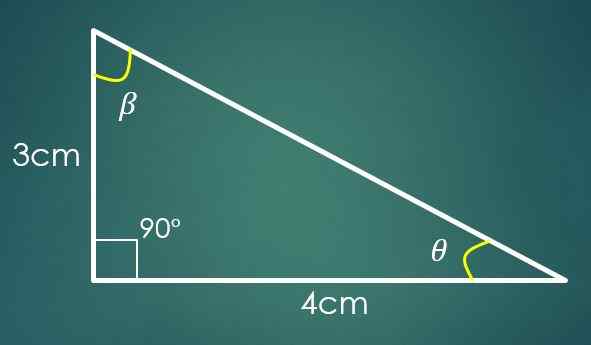
1- As duas pernas são conhecidas

Se o Cateto "A" mede 3 cm e o Cateto "B" mede 4 cm, para calcular o valor de "C", o teorema de Pitágoras é usado. Ao substituir os valores de "A" e "B", é obtido que C² = 25 cm², o que implica que C = 5 cm.

Agora, se o ângulo β for oposto à categoria "B", então sin (β) = 4/5. Ao aplicar a função reversa da mama, nesta última igualdade, é obtido que β = 53,13º. Dois ângulos internos do triângulo já são conhecidos.

Seja θ o ângulo que ainda precisa ser conhecido, então 90º+53,13º+θ = 180 °, onde é obtido que θ = 36,87º.

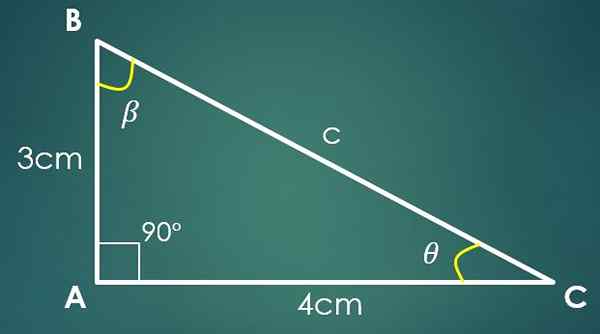
Nesse caso, não é necessário que os lados conhecidos sejam as duas pernas, o importante é saber o valor de dois lados.

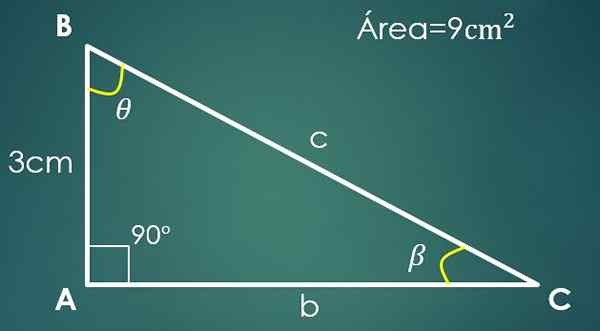
2- uma perna e a área é conhecida

Deixe A = 3 cm a perna conhecida e 9 cm² A área do triângulo.

Em um triângulo retângulo, uma categoria pode ser considerada base e a outra como altura (uma vez que são perpendiculares).

Suponha que "a" seja a base, portanto, 9 = (3 × h)/2, onde é obtido que a outra categoria mede 6 cm. Para calcular a hipotenusa, prossiga como no caso anterior, e é obtido que C = √45 cm.

Agora, se o ângulo β for oposto ao "A" Cateto, então sin (β) = 3/√45. Ao limpar β, é obtido que seu valor é 26,57º. Você só precisa saber o valor do terceiro ângulo θ.

É cumprido que 90 °+26,57º+θ = 180 °, onde se conclui que θ = 63,43º.

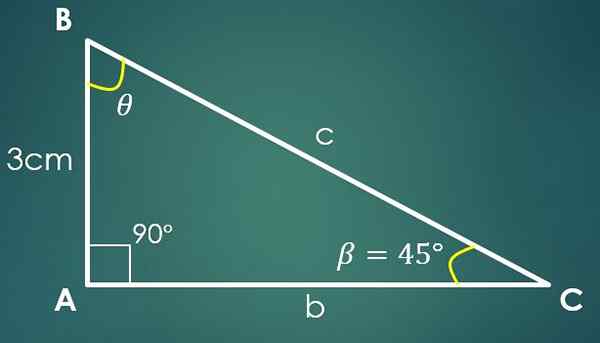
3- Um ângulo e um Cateto é conhecido

Seja β = 45 ° o ângulo conhecido e a = 3 cm a perna conhecida, onde o cateto “A” se opõe ao ângulo β. Usando a fórmula tangente, obtém -se que TG (45 °) = 3/CA, onde acontece que CA = 3 cm.

Usando o teorema de Pitágoras, obtém -se que c² = 18 cm², ou seja, c = 3√2 cm.

Sabe -se que um ângulo mede 90 ° e que β mede 45 °, a partir daqui conclui que o terceiro ângulo mede 45 °.

Nesse caso, o lado conhecido não precisa ser uma perna, pode ser qualquer um dos três lados do triângulo.