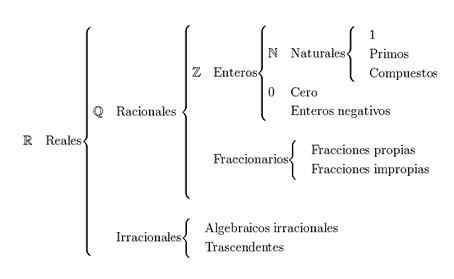
Classificação de números reais

Principal Classificação de números reais É dividido em números naturais, números inteiros, números racionais e números irracionais. Os números reais são representados com a letra r.

Números reais se referem à combinação de grupos de números racionais e irracionais. Para formar esses grupos, números naturais e números inteiros são necessários.

Existem muitas maneiras pelas quais os diferentes números reais podem ser construídos ou descritos, variando de formas mais simples a formas mais complexas, dependendo do trabalho matemático que você deseja executar.

Como os números reais são classificados?

- Números naturais

Os números naturais são representados pela letra (n) e são aqueles usados ​​para contar (0,1,2,3,4 ...). Por exemplo "existe quinze Rosas no jardim ",“ A população do México é de 126 milhões das pessoas "ou" a soma de dois e dois é quatro". Deve -se notar que algumas classificações incluem 0 como um número natural e outras não. 

Duas crianças fazendo uma soma de dois números naturais.

Os números naturais não incluem aqueles que têm uma parte decimal. Portanto, “a população do México é de 126.2 milhões de pessoas "ou" fazem uma temperatura de 24.5 Números naturais de Celsius graus ”não poderiam ser considerados.

Na linguagem comum, como escolas primárias, números naturais podem ser chamados de números contábeis para excluir números inteiros negativos e zero.

Números naturais são as bases com as quais muitos outros conjuntos de números podem ser construídos por extensão: números inteiros, números racionais, números reais e números complexos, entre outros.

As propriedades dos números naturais, como a divisibilidade e distribuição dos números primários, são estudados na teoria dos números. Os problemas relacionados à contagem e pedidos, como enumerações e partição, são estudados no combinador.

Eles têm várias propriedades, como: soma, multiplicação, subtração, divisão, etc.

Pode atendê -lo: ciência contemporânea

Números ordinais e cardinais

Os números naturais podem ser ordinais ou cardinais.

Os números cardinais seriam aqueles que são usados ​​como números naturais, como mencionado acima nos exemplos. "Ter dois biscoitos "," eu sou o pai de três crianças ",“ A caixa inclui dois cremes para presentes ". 

Ordinais são aqueles que expressam ordem ou indicam uma posição. Por exemplo, em uma corrida, a ordem de chegada dos corredores é listada pelo vencedor e terminando o último que chegou à linha de chegada.

Dessa forma, será dito que o vencedor é o "primeiro", o próximo "segundo", o próximo "terceiro" e assim por diante até o último. Esses números podem ser representados por uma letra no canto superior direito para simplificar a escrita (1ª, 2ª, 3ª, 4ª, etc.).

- Números inteiros

Todos os números são compostos desses números naturais e seus opostos, ou seja, os números negativos (0, 1, -1, 2, -2, 50, -50 ...). Como números naturais, eles não incluem aqueles que têm uma parte decimal.

Exemplo de números inteiros seria "média 30º na Alemanha", "fiquei em 0 ao chegar ao fim do mês", "para descer para o porão, você deve marcar o botão do elevador" do elevador ".

Por sua vez, números inteiros não podem ser escritos com um componente fracionário. Por exemplo, números como 8.58 ou √2 não são números inteiros.

Números inteiros são representados com a letra (z). Z é um grupo de subailas de números racionais q, que, por sua vez. Como números naturais, Z é um grupo contábil infinito.

Os números inteiros formam o menor grupo e o menor conjunto de números naturais. Na teoria dos números algébricos, números inteiros às vezes são chamados de irracionais para distingui -los de números inteiros algébricos.

Pode servir a você: Projeto de pesquisa: Partes, como é elaborado e exemplo

- Números racionais

O conjunto de números racionais é representado pela letra (Q) e inclui todos os números que podem ser escritos como uma fração de números inteiros.

Ou seja, este conjunto inclui números naturais (4/1), números inteiros (-4/1) e números decimais exatos (15,50 = 1550/100).

A distribuição de 1/6 de queijo é um número racional.

A expansão decimal de um número racional sempre termina após um número finito de dígitos (por exemplo, 15.50) ou quando a mesma sequência finita de dígitos começa a ser repetida repetidamente (por exemplo, 0,3456666666666666…). Portanto, dentro do conjunto de números racionais, os números estão incluídos. jornais puros ou jornais mistos.

Além disso, qualquer decimal repetido ou terminal representa um número racional. Essas declarações são verdadeiras não apenas para a base 10, mas também para qualquer outro número base.

Um número real que não é racional é chamado de irracional. Os números irracionais incluem √2, π e e, por exemplo. Como todo o conjunto de números racionais é entorpecido e que o grupo de números reais não é entorpecido, pode -se dizer que quase todos os números reais são irracionais.

Os números racionais podem ser formalmente definidos como classes de equivalência de pares inteiros (P, Q), de modo que q ≠ 0 ou a relação equivalente definida por (P1, Q1) (P2, Q2) apenas se P1, Q2 = P2Q1.

Os números racionais, juntamente com a soma e multiplicação, formam campos que compõem os números inteiros e estão contidos por qualquer ramo que contenha todo.

- Números irracionais

Números irracionais são números reais que não são números racionais; Números irracionais não podem ser expressos como frações. Os números racionais são os números compostos de frações de números inteiros.

Como conseqüência do teste do cantor que diz que todos os números reais não são inumeráveis ​​e que o racional se forem números, pode -se concluir que quase todos os números reais são irracionais.

Pode atendê -lo: trajetória e deslocamento

Quando o raio de dois segmentos de linha é um número irracional, pode -se dizer que esses segmentos de linha são incomensuráveis; o que significa que não há um comprimento suficiente para que cada um deles possa ser "medir" com um número inteiro múltiplo do mesmo.

Entre os números irracionais estão o raio π de um círculo de círculo ao seu diâmetro, o número de Euler (e), o número de ouro (φ) e a raiz quadrada de dois; Ainda mais, todas as raízes quadradas dos números naturais são irracionais. A única exceção a esta regra são os quadrados perfeitos.

Pode -se observar que quando números irracionais são expressos em posição em um sistema numeral (como números decimais) não terminam ou repetem.

Isso significa que eles não contêm uma sequência de dígitos, a repetição pela qual uma linha de representação é feita.

Simplificação do número irracional pi.

Por exemplo: a representação decimal do número π começa com 3.14159265358979, mas não há número finito de dígitos que possa representar π exatamente, nem eles podem ser repetidos.

A prova de que a expansão decimal de um número racional deve terminar ou repetir é diferente da prova de que uma extensão decimal deve ser um número racional; Embora básico e um pouco longo, esses testes levam algum trabalho.

Geralmente os matemáticos geralmente não tomam a noção de "final ou repetição" para definir o conceito de um número racional.

Números irracionais também podem ser tratados por meio de frações não contínuas.

Referências

1. Classificar números reais. Recuperado de Chilimath.com.
2. Número natural. Recuperado da Wikipedia.org.
3. Classificação de números. Ditutor recuperado.com.
4. Recuperado da Wikipedia.org.
5. Número irracional. Recuperado da Wikipedia.org.