Se chama Números significativos à quantidade de dígitos que contém o Mantisa de um número. Quanto mais números a quantidade é conhecida com a maior precisão. Como lembrete, o Mantisa é a figura que acompanha o poder de 10 quando o número na notação científico é escrito.

Por exemplo, vamos levar o número 0.00376, que está escrito como 3.76 x 10 ^-3. O Mantisa é 3.76 e o ​​número tem um total de 3 números significativos. O número 0.129 também tem 3 números significativos, enquanto 4.5 tem apenas 2.

figura 1. Calculadoras científicas nunca mostram o número de números significativos de uma operação. Fonte: piqsels.

E o que acontece quando o número é inteiro? Isso significa que é conhecido com toda a precisão possível, em outras palavras, tem precisão infinita. Por exemplo, contando pessoas, animais ou objetos como livros e telefones, o resultado é um número inteiro e preciso.

Se dissermos que em um cinema há 110 pessoas assistindo a um filme, esse é o número exato, nem mais nem menos, e tem 3 números significativos.

Números significativos são tratados por algumas regras simples que são memorizadas com um pouco de prática, como veremos então.

[TOC]

Regras para determinar os números significativos de um número

Regra 1

Os zeros anteriores não contam como um número significativo, então 0.045 e 4.5 Eles têm dois números significativos, já que eles começam a ser contados a partir da esquerda e começando a partir do primeiro dígito diferente de zero.

Regra 2

Os zeros posteriores (à direita) para o primeiro dígito significativo contam como uma figura significativa (desde que seja justificada pela precisão do instrumento de medição).

Finalmente, os zeros que estão no meio também são contados como um dígito significativo.

Regra 3

Para os números escritos em notação científica, todas as figuras da Mantisa são significativas e o expoente não influencia a precisão.

Pode atendê -lo: velocidade média: fórmulas, como é calculado e resolvido

Regra 4

Quando as operações com decimais são feitas, por exemplo, calculando áreas ou outras operações semelhantes, o resultado deve ter o mesmo número de números significativos que a quantidade com o menor número de números significativos que participaram da operação. Esta regra é válida para qualquer operação aritmética.

Regra 5

O número do número não influencia seu número de números significativos.

Veremos imediatamente alguns exemplos desta e de todas as outras regras.

Exemplos

Exemplo 1

Descubra quantos números significativos existem em cada um desses números.

a) 876

b) 1000.68

c) 0.00005026

d) 4.8

e) -6.99

Respostas

a) 876 tem 3 números significativos.

b) 1000.68 tem 6 números significativos, já que os zeros na contagem média como tal.

c) em vez de 0.00005026 tem 4 números significativos. Observe que os 5 zeros à esquerda dos 5 não são contados como um número significativo, em vez do 0 entre 5 e 2 sim.

d) 4.8 tem 2 números significativos.

e) -6.99 tem 3 números significativos.

Exemplo 2

É comum tomar medidas de medidas, como fitas métricas, relógios, termômetros, escalas e assim por diante. Quantos números significativos devemos relatar os valores que medimos dessa maneira?

Responder

Depende da apreciação do instrumento com o qual é medido. Vamos dar um exemplo: meça o diâmetro externo de um tubo, com uma regra graduada e com o pé de Vernier ou King.

O Vernier é um instrumento que mede o comprimento muito precisamente porque possui uma escala extra pequena, chamada Vernier, o que permite maior finura, por assim dizer, ao medir.

É mais preciso do que uma regra graduada, porque com ela podemos aprender números mais significativos de um certo comprimento.

É por isso que não faz sentido relatar um perímetro de, digamos, 35.88 cm Se medirmos com fita métrica, pois este instrumento não é preciso o suficiente para relatar tantos dígitos significativos.

Pode atendê -lo: estático: história, que estudos, aplicações, leis

A apreciação de uma fita é dada por:

Para uma fita métrica ou uma regra milímetro, a = 1 mm, que é o décimo de um centímetro. O perímetro medido com fita adesiva deve ser relatado como 35.9 cm.

Exemplo 3

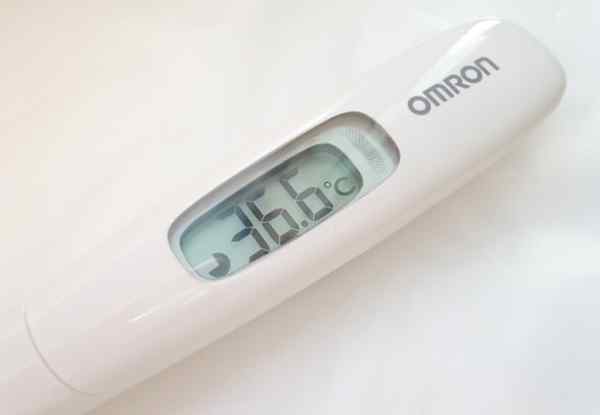
Quantas figuras significativas a leitura feita com o termômetro digital tem?

Responder

O termômetro da figura oferece leituras de temperatura com três dígitos. No entanto, na medida em que mostrado, 36.6 ºC, apenas os dois primeiros dígitos da esquerda para a direita são precisos, uma vez que o decimal é afetado pelo erro de apreciação do instrumento, que geralmente é indicado na parte traseira do mesmo ou em seu manual de operações.

A coisa usual para o tipo de instrumento digital mostrado é um erro de 0 apreciação.1 ºC. Isso é suficiente para ter certeza de que não há febre.

Figura 2. Termômetro digital cujas leituras são 3 números significativos. Fonte: pxhere.

Regras para números redondos

Quando uma calculadora é usada para executar cálculos com medidas obtidas, não está correto para fornecer o resultado usando todos os dígitos que aparecem na tela.

Somente aqueles que se conhecem com precisão são retidos, porque apenas esses têm um significado verdadeiro. Então é necessário arredondar os resultados para ajustar o número de números conhecidos precisamente. Essas regras são:

-Se o número a seguir o dígito a ser retido for igual ou superior a 5, A este dígito é adicionado 1.

Por exemplo, arredondando 3.786 Para ter dois decimais, queremos manter os números até 8. Como o número a seguir (6) é maior que 5, o 8 se torna 8 + 1 = 9 e o número permanece 3.79.

-Quando o número após o dígito a ser retido é menos de 5, O dígito é o mesmo.

Pode servir a você: Efeito Joule: Explicação, Exemplos, Exercícios, Aplicações

Se queremos a rodada 1.27924 Para ter apenas 3 decimais, isso é alcançado atingindo 9, que é seguido por um 2. Como o 2 é menor que 5, esses decimais desaparecem e o número arredondado é 1.279.

Exercício resolvido

Uma mesa de jantar tem a forma e as dimensões indicadas na figura em anexo. É solicitado a calcular sua área usando as regras de operações com números significativos.

Solução

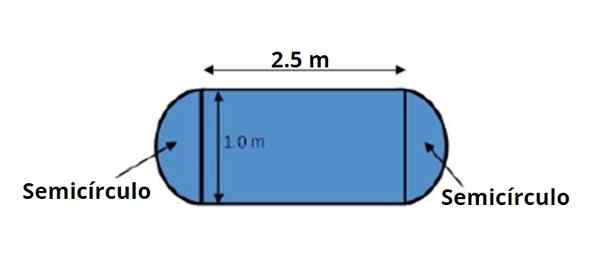Figura 3. Uma tabela tem a forma e as dimensões indicadas na figura, observe que elas são conhecidas com duas figuras significativas. Fonte: f. Zapata.

A área da mesa pode ser dividida em uma área retangular central e dois semicírculos, um de cada lado, que juntos fazem 1 círculo completo.

Vamos ligar₁ para a área do retângulo, dada por:

PARA₁ = base × altura = 2.5 m x 1.0 m = 2.5m²

Por sua parte, a área do círculo, que é equivalente à de 1 semicírculo multiplicada por 2 é:

PARA₂ = π × rádio²

O diâmetro de qualquer um dos semicírculos é 1.0 m, portanto o raio é 0.50 m. O diâmetro também pode ser usado diretamente para calcular a área, neste caso:

PARA₂ = (π × diâmetro²) / 4

Em todo caso:

PARA₂ = [π x (1.0 m)²] / 4 = 0.785398163 m²

Todos os dígitos oferecidos pela calculadora foram usados. Agora adicionamos a₁ já₂ Para a área total da tabela:

A = (2.5 + 0.785398163) m² = 3.285398163 m²

Como as dimensões da tabela são conhecidas com 2 números significativos, não faz sentido expressar o resultado com todos os decimais dados pela calculadora, o que nunca fornece o número de números significativos de um resultado.

O que precisa ser feito é arredondar a área para ter o mesmo número de números significativos que as dimensões da tabela, ou seja, 2. Portanto, o resultado final é relatado assim:

A = 3.3 m²

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
3. Fisicalab. Números significativos e arredondamento. Recuperado de: fisicalab.com.
4. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.