Processo de ciclo de Brayton, eficiência, aplicações, exercícios

Ele Ciclo de Brayton É um ciclo termodinâmico que consiste em quatro processos e se aplica a um fluido termodinâmico compressível como um gás. Sua primeira menção data do final do século 18, embora ele tenha passado algum tempo antes de ser criado por James Joule. É por isso que também é conhecido como o ciclo Joule.

Consiste nos seguintes estágios, que são convenientemente ilustrados no diagrama de pressão - volume da Figura 1: Compressão adiabática (sem calor é trocado), expansão isobárica (ocorre a pressão constante), expansão adiabática (nenhum calor é trocado) e compressão isobárica (ocorre a pressão constante).

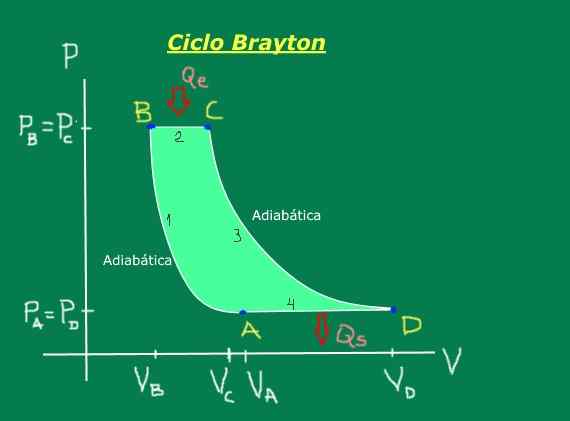figura 1. Ciclo de Brayton. Fonte: Self feito.

[TOC]

Processo e descrição

O ciclo de Brayton é o ciclo termodinâmico ideal que é melhor aplicado para explicar o funcionamento termodinâmico de turbinas a gás e mistura o combustível de ar, usado para a geração de eletricidade e nos motores da aviação.

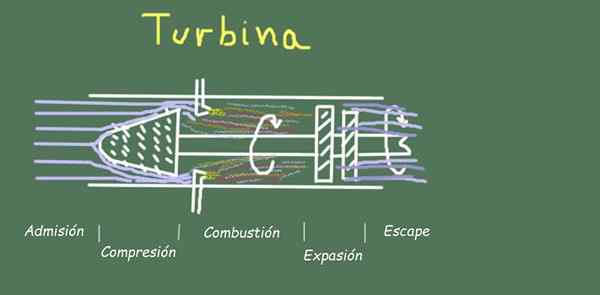Figura 2. Esquema de turbina e estágios de fluxo. Fonte: Self feito.

Por exemplo, na operação de uma turbina, existem vários estágios no fluxo de gás da operação, que veremos abaixo.

Admissão

Consiste na entrada de ar à temperatura e pressão ambiental devido à abertura da turbina.

Compressão

O ar é comprimido por paletas giratórias contra outras fixadas na seção do compressor de turbina. Essa compactação é tão rápida que praticamente não há troca de calor, por isso é modelada através do processo Brayton Cycle AB. O ar na saída do compressor aumentou sua pressão e temperatura.

Combustão

O ar é misturado com gás propano ou combustível em pó que é introduzido pelos injetores da câmara de combustão. A mistura produz uma reação de combustão química.

Essa reação é a que fornece o calor que aumenta a temperatura e a energia cinética das partículas de gás que se expandem na câmara de combustão à pressão constante. No ciclo de Brayton, esta etapa é modelada com o processo BC que ocorre a pressão constante.

Expansão

Na seção da própria turbina, o ar continua a se expandir contra as paletas da turbina, fazendo -a girar e produzir trabalho mecânico. Nesta etapa, o ar diminui sua temperatura, mas sem trocar calor praticamente com o ambiente.

No ciclo de Brayton, esta etapa é simulada como um CD do processo de expansão adiabática. Parte do trabalho da turbina é transferida para o compressor e o outro é usado para mover um gerador ou uma hélice.

Escape

O ar de saída está sob pressão constante igual a ambiental e produz calor para a enorme massa de ar externo; portanto, em pouco tempo, leva a mesma temperatura do ar de entrada. No ciclo de Brayton, esta etapa é simulada com o processo de pressão constante, fechando o ciclo termodinâmico.

Eficiência com base na temperatura, calor e pressão

Propomos calcular a eficiência do ciclo de Brayton, para o qual começamos a partir da definição do mesmo.

Em uma máquina térmica, a eficiência é definida como o trabalho líquido realizado pela máquina dividida pela energia térmica fornecida.

Pode servir a você: reflexão leve

O primeiro princípio da termodinâmica estabelece que o calor líquido contribuiu para um gás em um processo termodinâmico é igual à variação da energia interna do gás, mais o trabalho realizado pelo mesmo.

Mas em um ciclo completo, a variação de energia interna é nula, por isso tem que o calor líquido contribuído no ciclo é igual ao trabalho líquido realizado.

Calor recebido, calor e eficiência de saída

A expressão anterior nos permite escrever eficiência com base no calor absorvido ou recebido (positvo) e no calor atribuído ou de saída (negativo).

Calor e pressão no ciclo de Brayton

No ciclo de Brayton, o calor entra no processo isobárico BC e sai no processo isobárico.

Supondo que não de pressão constante fornecida com calor sensível que, no processo BC, sua temperatura aumenta de TB para TC de acordo com o seguinte relacionamento:

Onde cp É a capacidade de calor a pressão constante.

O calor extrovertido QS Pode ser calculado da mesma forma pelo relacionamento a seguir que se aplica ao processo a pressão constante fornece:

Substituindo essas expressões na expressão que nos dá eficiência com base na entrada de calor e calor, fazendo as simplificações pertinentes, é obtido o seguinte relacionamento para eficiência:

Resultando em que a eficiência é independente da massa de ar que passa pela turbina.

Resultado simplificado

É possível simplificar o resultado anterior se levarmos em consideração que PA = PD e que PB = PC Como os processos de AD e BC são Isobárica, isto é, na mesma pressão.

Além disso, como os processos AB e CD são adiabáticos, o relacionamento de Poisson para ambos os processos é cumprido:

Onde Gama representa o quociente adiabático, ou seja, o quociente entre a capacidade de calor à pressão constante e a capacidade de calor em volume constante.

Usando esses relacionamentos e a relação da equação do estado de um gás ideal, podemos obter uma expressão alternativa para o relacionamento de Poisson:

Como sabemos disso PA = PD e que PB = PC Substituindo e dividindo membro ao membro, é obtido o seguinte relacionamento entre temperaturas:

Se cada membro da equação anterior for subtraído da unidade, a diferença é resolvida e os termos são fixos, pode -se demonstrar que:

Para que a eficiência possa ser escrita em função da temperatura do ar na entrada e temperatura do ar no final do processo de compressão AB.

Desempenho dependendo da taxa de pressão

A expressão obtida para a eficiência do ciclo de Brayton com base em temperaturas pode ser reescrita para ser formulada com base na taxa de pressão na saída e entrada do compressor.

Isso é alcançado se a relação de Poisson entre os pontos A e B for conhecida dependendo da pressão e da temperatura, obtendo que a eficiência do ciclo é expressa da seguinte maneira:

Pode servir a você: pressão relativa: fórmula, como é calculado, exemplos, exercícios

Sendo o quociente entre PB e PA.

Uma taxa de pressão típica é 8. Nesse caso, o ciclo Brayton tem um desempenho teórico de 45%.

Formulários

O ciclo de Brayton como modelo se aplica a turbinas a gás usadas em usinas termoelétricas, a fim de mover os geradores que produzem eletricidade.

É também um modelo teórico que se encaixa bem na operação de motores turbo -herdeiros usados ​​em aviões, mas não é aplicável em todos os turboreatores de aeronaves.

Quando está interessado.

Figura 3. Motor de turbofan mais eficiente que o turbororador. Fonte: Pixabay

Nos turboreactos de aeronaves, por outro lado, não está interessado.

Pelo contrário, está interessado.

Exercícios resolvidos

-Exercício 1

Uma turbina a gás usada em usinas termoelétricas tem uma pressão na saída de 800 kPa de compressor. A temperatura do gás de entrada é o meio ambiente e é 25 Celsius, e a pressão é de 100 kPa.

Na câmara de combustão, a temperatura sobe para 1027 Celsius para entrar na turbina.

Determine a eficiência do ciclo, a temperatura do gás fora do compressor e a temperatura do gás na saída da turbina.

Solução

Como temos a pressão do gás na produção do compressor e sabemos que a pressão de entrada é pressão atmosférica, por isso é possível obter a taxa de pressão:

R = pb / pa = 800 kPa / 100 kPa = 8

Como o gás com o qual a turbina opera é uma mistura de ar e gás de propano, o coeficiente adiabático para um gás diatômico ideal é então aplicado, ou seja, uma gama de 1.4.

A eficiência seria então calculada assim:

Onde aplicamos o relacionamento que dá a eficiência do ciclo de Brayton, dependendo da taxa de pressão no compressor.

Cálculo da temperatura

Para determinar a temperatura na saída do compressor, ou qual é a mesma temperatura com a qual o gás entra na câmara de combustão, aplicamos a taxa de relacionamento com a entrada de entrada do compressor e temperaturas de saída.

Se limparmos a temperatura da TB dessa expressão, obtemos:

Em outras palavras, a temperatura de pré -combate é 804,12 Celsius.

À medida que o exercício do exercício, depois de combustão, a temperatura aumenta para 1027 Celsius, para entrar na turbina. Parte da energia térmica do gás é usada para mover a turbina, de modo que a temperatura na saída dela deve ser menor.

Pode atendê -lo: aplicações de energia, poder, força, conceitos de trabalho

Para calcular a temperatura na saída da turbina, usaremos uma proporção entre a temperatura anteriormente:

A partir daí, limpamos o TD para obter a temperatura na saída da turbina. Depois de executar os cálculos, a temperatura obtida é:

TD = 143,05 Celsius.

-Exercício 2

Uma turbina a gás segue o ciclo de Brayton. As pressões entre a partida e a entrada do compressor são 12.

Suponha a temperatura ambiente de 300 K. Como dados adicionais, sabe -se que a temperatura do gás após a combustão (antes da entrada da turbina) é de 1000k.

Determine a temperatura na saída do compressor e a temperatura na saída da turbina. Determine também quantos quilos de gás circulam através da turbina a cada segundo, sabendo que o poder é de 30 kW.

Suponha o calor específico do gás como constante e pegue o valor dele à temperatura ambiente: cp = 1.0035 j / (kg k).

Suponha também que a eficiência da compressão no compressor e a descompressão na turbina seja 100%, o que é uma idealização, porque na prática as perdas sempre ocorrem.

Solução

Para determinar a temperatura na saída do compressor, conhecido a temperatura na entrada, devemos lembrar que é uma compressão adiabática; portanto, o relacionamento de Poisson para o processo AB pode ser aplicado.

Dessa forma, obtemos que a temperatura da TB na saída do compressor é dada por:

Da mesma forma, a descompressão dos gases que atravessam a turbina é um processo adiabático que corresponderia ao processo do ciclo de Brayton. Portanto, podemos aplicar a proporção de Poisson para obter a temperatura da saída da turbina.

Para qualquer ciclo termodinâmico, o trabalho líquido sempre será igual ao calor líquido trocado no ciclo.

No relacionamento anterior, que é o calor (positivo) e QS do calor (negativo) (negativo). No ciclo de Brayton, essas trocas ocorrem os processos BC e DA, ambos isobácos.

Trabalho líquido por ciclo de operação pode ser expresso dependendo da massa de gás que circulou nesse ciclo e temperaturas.

Nesta expressão m É a massa de gás que circulou pela turbina em um ciclo de operação e Cp O calor específico.

Se tomarmos o derivado em relação ao tempo da expressão anterior, obtemos a potência média líquida com base no fluxo de massa.

Limpeza m ponto, e substituindo as temperaturas, a potência e a capacidade de calor do gás, obtemos um fluxo de massa de 1578,4 kg/s.

Referências

1. Alfaro, J. Ciclos termodinâmicos. Recuperado de: fis.Puc.Cl.
2. Fernández J.F. Ciclo de Brayton. Turbina a gás. OU.T.N. (Mendoza). Recuperado de: edutecne.Utn.Edu.ar.
3. Universidade Sevilla. Departamento de Física. Ciclo de Brayton. Recuperado de: Laplace.nós.é.
4. Universidade Experimental Nacional da Táchira. Fenômenos de transporte. Ciclos de energia a gás. Recuperado de: UNET.Edu.ir.
5. Wikipedia. Ciclo de Brayton. Recuperado de: wikiwand.com
6. Wikipedia. Turbina a gás. Recuperado de: wikiwand.com.