Unidades de capacitância, fórmulas, cálculo, exemplos

O Capacitância É a relação entre a carga de um capacitor ou treinador, medido em Coulomb, e seu potencial ou tensão elétrica, medido em volts. É expresso nas unidades Faradio (f), em homenagem a Michael Faraday (1791-1867).

A capacitância também é definida como propriedade ou capacidade de um condensador ou conjunto de capacitores elétricos, que é medido pela quantidade de carga elétrica que pode ser armazenada, separadamente, por unidade de mudança do potencial elétrico.

As lâmpadas, assim como qualquer outro dispositivo elétrico, devem parte de sua operação para a capacitância. Fonte: Pixabay.

O termo capacitância é introduzido como resultado da criação de um dispositivo elétrico chamado capacitor, inventado pelo cientista prussiano Ewald Georg von Kleist, em 1745, e independentemente do físico holandês Pieter Van Musschenbroek.

Os capacitores são dispositivos elétricos que armazenam carga elétrica e baixam instantaneamente. Esta propriedade tem sido usada em vários dispositivos elétricos, como televisão, rádio, lâmpadas, computador, entre muitos outros na vida cotidiana.

[TOC]

Capacitor e capacitância

Um capacitor ou capacitor é composto por dois motoristas que têm cargas iguais e de outra forma. Os motoristas são chamados de armaduras de armadura ou condensador.

Uma placa está ligada ao terminal positivo (+) de uma bateria, enquanto a outra placa está ligada ao negativo (-). Como as placas têm cargas iguais e o sinal oposto, a carga líquida de um capacitor é zero (0).

Capacitância é a relação entre a carga de um motorista ou condutores que formam um capacitor e o valor da diferença de tensão entre as placas do condensador.

Pode atendê -lo: refrigerante Rosario

Unidades e fórmulas

A fórmula de capacitância é a seguinte:

C = Q / V

Onde C é capacitância, q a carga (cuja unidade é o Coulomb) e v  A tensão (volt)

A unidade de capacitância é o Faradio (F), que é equivalente a Coulomb / Voltio. O Faradio é uma unidade muito grande; portanto, o microfradio (µF) é usado, equivalente a 10^-6 farad; ou o pico de Faradio (PF), que é equivalente a 10^-12 farad.

Como a capacitância é calculada?

Qual será o valor da capacitância de um capacitor cujas placas têm uma carga de 5,10^-3 Coulomb e uma diferença de tensão de 6 volts?

Aplicando a fórmula que resolvemos:

C = Q / V

= (5 · 10^-3 Coulomb) / (6 volts)

= 8,33 · 10^-4  farad

Exemplos

A fórmula de capacitância varia dependendo do tipo de capacitor.

Capacitor de placas paralelas

C = Kε_qualquerDe Anúncios

k é a constante dielétrica, que tem um valor de 1 no ar e o vazio. Por esse motivo, a fórmula é reduzida a:

C = ε_qualquerDe Anúncios

ε_qualquer É a constante dielétrica, cujo valor é próximo de 8.854,10^-12 F · m^-1, A é a área ou superfície das placas paralelas expressas em m², enquanto d A distância que separa as placas paralelas.

Capacitor esférico

C = 4πε_qualquerR

Onde r é o raio da esfera em medidores.

Esferas concêntricas

C = 4πε_qualquer / (1/ r₁ - 1/r₂)

Capacitor de cilindro concêntrico

C = 2πε_qualquerl/ln (r₂ / R₁)

Onde eu é a duração dos cilindros concêntricos em metros.

Exercícios resolvidos

Capacitor de placas planas paralelas

Qual será a capacidade de um capacitor ou capacitor no ar com uma área de suas placas de 3 cm² e separado por uma distância de 2 mm?

Pode atendê -lo: 12 exemplos de bases químicas

Temos a fórmula:

C = ε_qualquerDe Anúncios

E os dados:

ε_qualquer = 8.854 x 10^-12 F · m^-1

A = 3 cm² (3 · 10^-4 m²)

D = 2 mm (2,10^-3 m)

Prossiga substituir:

C = (8.854 · 10^-12 F · m^-1) (3 · 10^-4 m²) / (2 · 10^-3 m)

= 1.3281 · 10^-14 F

Capacitor ou capacitor em forma de esfera

Se a Terra é considerada um capacitor esférico com um raio (r) de 6.370 km: qual será o valor da sua capacitância?

Dados:

C = 4πε_qualquerR

Π = 3.1416

ε_qualquer = 8.854 · 10^-12 F.m^-1

R = 6.370 km (6,37 · 10⁶ m)

Os valores na fórmula da capacitância são substituídos novamente:

C = (4, 3.1416) (8.854,10^-12 F · m^-1) (6,37 · 10⁶ m)

= 7,09 · 10^-8 F

= 709 µF

Combinação de capacitores

Capacitores ou capacitores podem ser combinados em série ou em paralelo.

Capacitores da série

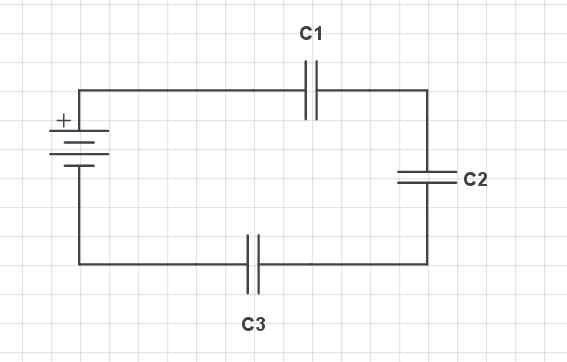Capacitores da série. Fonte de Gabriel Bolívar via circuito

A imagem superior mostra três capacitores da série (C₁, C₂ e C₃), bem como uma bateria com seus terminais positivos (+) e negativos (-). Esses capacitores têm uma série de características em relação à sua tensão, carga e capacitância.

Queda de tensão (ΔV) em capacitores

ΔV_t = ΔV₁   +   ΔV₂   +    ΔV₃

A queda total de tensão em um conjunto de capacitores em série é igual à soma da tensão cai dos capacitores.

Fardo  de capacitores

Q_t = Q₁ = Q₂ = Q₃

A mesma quantidade de carga circula através da série.

Capacitores capacitância

A capacitância equivalente dos capacitores em série apresenta o seguinte relacionamento:

1 c_Eq  = 1/c₁  +   1 c₂   +   1 c₃

Capacitores paralelos

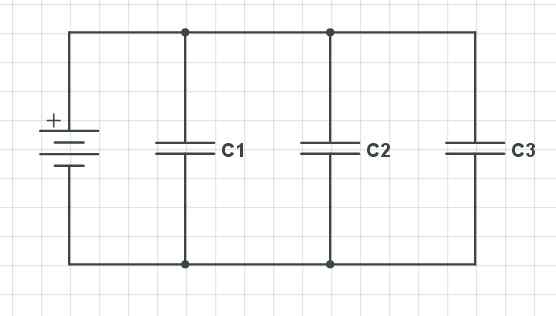Capacitores paralelos. Fonte de Gabriel Bolívar via circuito.

Up, temos três capacitores organizados em paralelo (C₁, C₂ e C₃), que mantêm em relação à queda de tensão, carga e capacitância o seguinte comportamento:

Pode atendê -lo: alcenos

Queda de tensão nos capacitores

ΔV_t  = ΔV₁  = ΔV₂  = ΔV₃

Em capacitores paralelos, a queda total de tensão nos capacitores é a mesma que a existente para cada um dos capacitores.

Capacitores

Q_t  = Q₁  +  Q₂  +  Q₃

Em um sistema em paralelo, o carregamento total dos capacitores é igual à soma da carga de todos os capacitores.

Capacitores capacitância

C_Eq  = C₁  +  C₂   +  C₃

Em um sistema paralelo, a capacitância equivalente deles é igual à soma das capacitâncias de todos os capacitores.

Exemplo de exercício

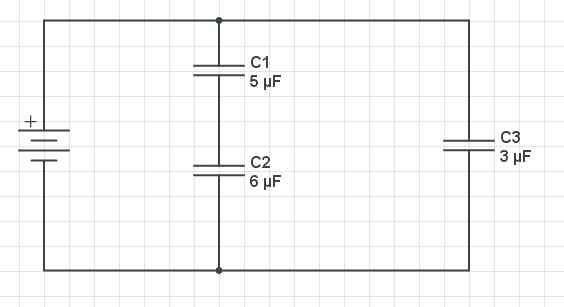Exemplo de um problema e problema de capacitores paralelos. Fonte de Gabriel Bolívar via circuito.

Um esquema de três capacitores é mostrado acima: C₁ e C₂ Eles estão organizados em série e estão em paralelo com C₃. A capacitância dos capacitores são os seguintes: C₁ = 5 µF, C₂ = 6 µF e C₃ = 3 µF. Encontre a capacitância equivalente do circuito.

Primeiro é a capacitância equivalente de C₁ e C₂ quem está em série.

1 c_EQ1,2 = 1/c₁  +  1 c₂

1 c_EQ1,2 = 1/5 µf +1/6 µf

1 c_EQ1,2 = (11/30) µF

C_EQ1,2 = 30 µF / 11

= 2,72 µF

Os capacitores 1 e 2 estão em paralelo com C₃. Então, a capacitância equivalente de C₁, C₂ e C₃ é igual a C_EQ1,2 +  C₃.

C_EQ1,2,3 = 2,72 µF +3 µF

= 5,72 µF

Referências

1. Serway, r. PARA. e Jewett, J. C. (2009). Física para Ciência e Engenharia. Volume 2. Sétima edição. Aprendizagem editorial do Cengage.
2. Reddick, R e Halliday, D. (1965). Físico.  Parte 2. Segunda edição em espanhol. Editorial continental s.PARA.
3. Estudar. (22 de abril de 2015). Capacitância: unidades e fórmula. Recuperado de: estudo.com
4. Física do Lumes. (s.F.). Capacitores em série e paralelos. Recuperado de: cursos.Lumenarning.com
5. Os editores da Enyclopaedia Britannica. (2020). Capacitância. Recuperado de: Britannica.com